Unit – 4

Unit – 4

Matrix Algebra- I

Q 1: 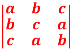   = (a+b+c) (ab+bc+ca-a2 –b2 –c2)

Solution:

By using invariance and scalar multiple property we can prove the given problem.

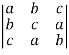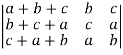=   =   c1 c1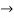+c2+c3

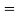(a+b+c)

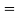(a+b+c)  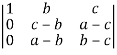 R2 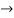R2 – R1 and R3 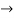R3 – R1

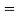(a+b+c)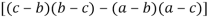

(a+b+c)(ab+bc+ca-a2-b2 –c2)

Q 2: Prove the following identity.,

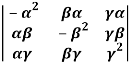= 4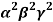

Solution:

Take 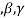, from the L.H.S and then by using scalar multiple property and in-variance property of determinant. We can prove the given problem

=

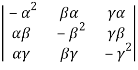
Taking, , 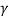common from c1, c2, c3 respectively

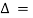
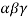
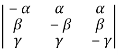
Now taking common from R1, R2, R3 respectively.

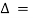
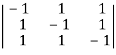
Now applying R3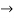  R3+R1 we have =

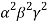
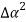
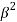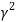Now expanding along c1,

  (-1)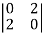 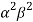(-1) =  (-1)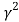 (0-4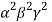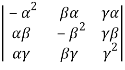) =4

      =4.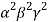

Hence proved.

Q 3: Reduce the following matrix into normal form and find its rank,

Solution: Let A =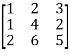

Apply 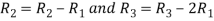we get

     A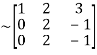 

Apply 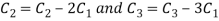we get

        A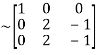 

Apply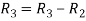

      A 

Apply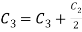

     A 

Apply 

     A 

Hence the rank of matrix A is 2 i.e. .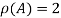

Q 4: Reduce the following matrix into normal form and find its rank,

Solution: Let A =   

Apply 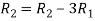and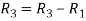

               A

Apply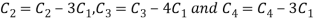

               A

Apply

                  A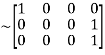

Apply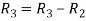

                     A

Apply

                      A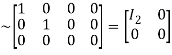

Hence the rank of the matrix A is 2 i.e. .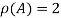

Q 5: Reduce the following matrix into normal form and find its rank,

Solution: Let A =

Apply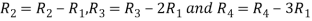

Apply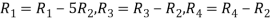

Apply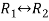

Apply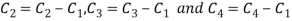 

Apply and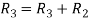

Apply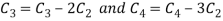

Hence the rank of matrix A is 2 i.e. .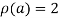

Q 6:  Diagonalize the matrix

Solution: Let A=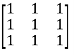

The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values .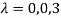

Then    and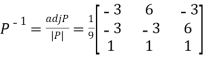

Also, we know that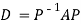    

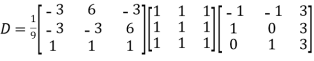
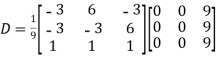
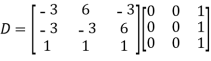
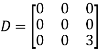
Q 7: Diagonalize the matrix

Solution: Let A =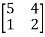

The Eigen vectors are (4,1),(1,-1) corresponding to Eigen values .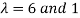

Then 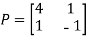   and also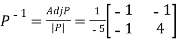 

Also, we know that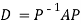    

Q 8: GIVEN 33 RECTANGULAR MATRIX

Solution: The augumented matrix is as follows

• After applying the Gauss-Jordan elimination method:

The inverse of a matrix is as follows.,

Q 9: Find the inverse of

A=    

Solution:

Step 1: Adjoin the identity matrix to the right side of A:

Step 2: Apply row operations to this matrix until the left side is reduced to I. The computations are:

              R2 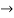 R2-R1  , R3 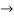R3-R1

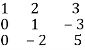
             R3 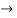R3 + 2R2

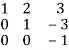
        R1R1 -3R3  , R2 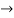R2+3R3

     R1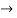R1-2R2

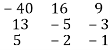
Step 3: Conclusion: The inverse matrix is:

A-1 =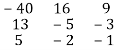

Q 10: Reduce the following matrix to normal form of Hence find it’s rank,

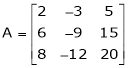
Solution:

We have,

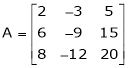
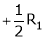
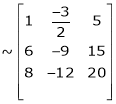
Apply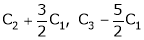

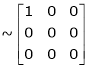
Rank of A = 1

Q 11: Find the rank of the matrix

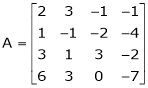
Solution:

We have,

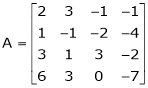
Apply R12

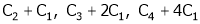
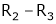
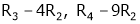
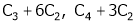
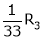
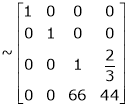
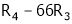
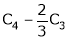
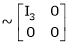
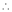Rank of A = 3

Q 12: Find the rank of the following matrices by reducing it to the normal form.

Solution:

Apply C14

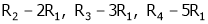
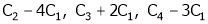
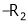
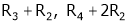
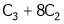
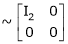
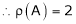
H.W.

Reduce the follo9wing matrices in to the normal form and hence find their ranks.

a)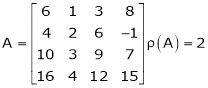    

b)   

1. Reduction of a matrix a to normal form PAQ.

If A is a matrix of rank r, then there exist a non – singular matrices P & Q such that PAQ is in normal form.

i.e.

To obtained the matrices P and Q we use the following procedure.

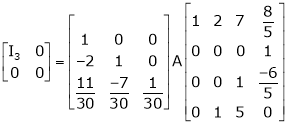
Q 13: If 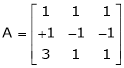Find Two

Matrices P and Q such that PAQ is in normal form.

Solution:

Here A is a square matrix of order 3 x 3. Hence, we write,

A = I3 A.I3

i.e.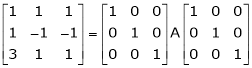

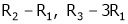
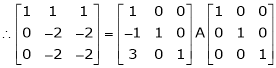
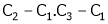
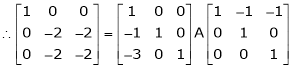
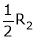
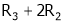
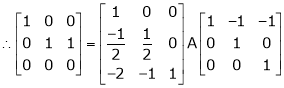
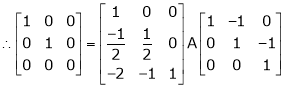
i.e.

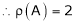
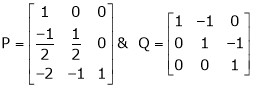
Q 14: Find a non – singular matrices p and Q such that P A Q is in normal form where

Solution:

Here A is a matrix of order 3 x 4. Hence, we write A as,

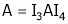
i.e.

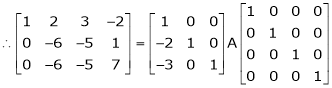
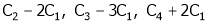
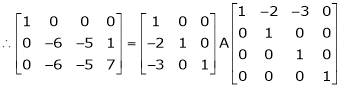
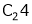
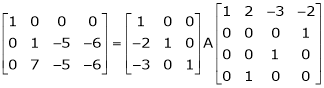
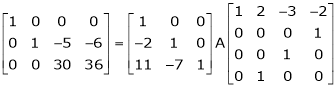
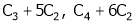
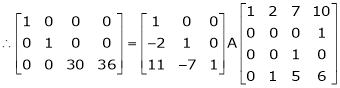
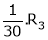
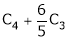
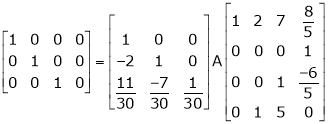
i.e.