ERROR ANALYSIS

UNIT -1

QUESTION BANK

1. Question The period of oscillation of a simple pendulum is T =2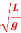  Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using a wrist watch of 1 s resolution. What is the accuracy in the g?

 Solution:

As

T =2   and g = 4π2(L/T2)

x 100 =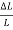 x 100 +2 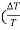x 100)

Now L=20.0cm, L=0.1cm, T for 100 oscillation = 90sec , T=1 sec

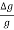x 100 = 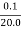x 100 +2 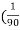x 100)=0.5 +2.22 =2.72% =3%

2. Question Find the relative error in Z, if Z=A4 B1/3 / CD3/2

Solution . In relative error in Z is

= 4 x + + +

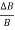3. Question: Mean refractive index is given as 1.29, 1.33, 1.34, 1.35 , 1.32 , 1.36,  1.30, 1.33 find absolute error, Mean Absolute error, Relative error  and Percentage error.

Solution:

Mean refractive index is average of eight values i.e.
μmean = (1.29 + 1.33 + 1.34 + 1.35 + 1.32 + 1.36 + 1.30 + 1.33) ÷ 8
μmean =10.62 ÷ 8 = 1.3275 ≈ 1.33.

Absolute error are:
Δμ1 = μmean – μ1  = 1.33 – 1.29 = 0.04
Δμ2 = μmean – μ2  = 1.33 – 1.33 = 0.00
Δμ3 = μmean – μ3  = 1.33 – 1.34 = -0.01
Δμ4 = μmean – μ4  = 1.33 – 1.35 = -0.02
Δμ5 = μmean – μ5  = 1.33 – 1.32 = 0.01
Δμ6 = μmean – μ6  =  1.33 – 1.36 = -0.03
Δμ7 = μmean – μ7  = 1.33 – 1.30 = 0.03
Δμ8 = μmean – μ8  =  1.33 – 1.33 = 0.00

Mean Absolute error  Δμmean
= (|Δμ1 | + |Δμ2 | + |Δμ3 | + | Δμ4 | + | Δμ5 | + | Δμ6 | + |Δμ7 | + |Δμ8 |) ÷ 8
= ( 0.04 + 0.00 + 0.01 + 0.02 + 0.01 + 0.03 + 0.03 + 0.00) ÷ 8
= 0.14 ÷ 8 = 0.0175 ≈  0.02

Relative error (δμ) =  Δμmean/ μmean = 0.02 ÷ 1.33 = ± 0.015 ≈ 0.02

Percentage error =  (Δμmean/ μmean) × 100% = ± 0.015 × 100 = ± 1.5

4. Question: How errors are propagated or combined?

Solution:

While applying mathematical operations (e.g. Addition, subtraction, multiplication and division) on physical quantities, errors are combined.

If A and B are two physical quantities represented as A ± ΔA and B ± ΔB, then
(a) In addition, i.e. Z = A + B, absolute error  ΔZ = ΔA + ΔB.

(b) In difference, Z = A – B, absolute error  ΔZ = ΔA + ΔB.

(c) In product, Z = AB, then absolute error  ΔZ/Z = ΔA/A + ΔB/B.

(d) In division, Z = A/B,  ΔZ/Z = ΔA/A + ΔB/B.

(e) In power, Z = Ax.By/Cz, then  ΔZ/Z = xΔA/A + yΔB/B ± zΔC/C

5. Question: A current of 3.5 ± 0·5 ampere flows through metallic conductor.  And a potential difference of 21 ± 1 volt is applied. Find the Resistance of the wire.

Solution:

Given V = 21± 1volts, ΔV = 1, I = 3.5 ± 0·5 A and ΔI = 0.5A
Resistance R  = V / I = 21± 1 / 3.5 ± 0·5 = 6 ± ΔR
ΔR/R = error in measurement = ΔV/V + ΔI/I = 1/21 + 0.5/3.5 = 0.048 + 0.143 = 0.191 ≈ 0.19
⇒ ΔR = 0.19 × R = 0.19 × 6 = 1.14

∴ Effective resistance R = 6 ± 1.14 Ω

6. Question: A rectangular board is measured with a scale having accuracy of 0.2cm. The length and breadth are measured as 35.4 cm and 18.4 cm respective. Find the relative error and percentage error of the area calculated.

Solution:

Given length (l) = 35.4 cm, Δl = 0.2cm
Width = 18.4cm and Δw = 0.2cm

Area (A) = l × w = 35.4 × 18.4 = 651.36 cm2

Relative error in Area (δA) = ΔA/A = Δl/l + Δw/w =0.2/35.4 + 0.2/18.4 = 0.006 + 0.011 = 0.017
Percentage error = ΔA/A × 100 = 0.017 × 100 = 1.7%

7. Question: What is relative error or percentage error?

Solution:

The relative error is the ratio of the mean absolute error Δamean to the mean value amean of the quantity measured.
i.e. Relative error = Δamean/ amean

When the relative error is expressed in per cent, it is called the percentage error (δa).
⇒  δa = (Δamean/ amean) × 100%

8. Question: How can we minimize errors?

Solution:

Using instruments of higher precision, improving experimental techniques, etc., we canr reduce the least count error.

Repeating the observations several times and taking the arithmetic mean of all the observations, the mean value would be very close to the true value of the measured quantity.

Gross errors can be minimized only if the observer is very careful in his observations and sincere in his approach.

9. Question: What is regression analysis ?

Solution:

Regression Analysis is a set of statistical processes for estimating the relationships between a dependent variable  and one or more independent variables.

Regression analysis is a powerful statistical method that allows you to examine the relationship between two or more variables of interest. 

In order to understand regression analysis fully, it’s essential to understand the following terms:

• Dependent Variable: This is the main factor that you’re trying to understand or predict. 
• Independent Variables: These are the factors that you hypothesize have an impact on your dependent variable.

Regression analysis is a statistical technique used to describe relationships among variables. The simplest case to examine is one in which a variable Y, referred to as the dependent or target variable, may be related to one variable X, called an independent or explanatory variable, or simply a regressor.

The simplest case to examine is one in which a variable Y, referred to as the dependent or target variable, may be related to one variable X, called an independent or explanatory variable, or simply a regressor. If the relationship between Y and X is believed to be linear, then the equation for a line may be appropriate:

Y=β1+β2X,

Where β1 is an intercept term and β2 is a slope coefficient.

In simplest terms, the purpose of regression is to try to find the best fit line or equation that expresses the relationship between Y and X.

10. Question: Discuss uses of regression ?

Solution:

Applications of regression are numerous and occur in almost every field, including engineering, the physical and chemical sciences, economics, management, life and biological sciences, and the social sciences. In fact, regression analysis may be the most widely used statistical technique

Regression models are used for several purposes, including the following: 

1. Data description

2. Parameter estimation

3. Prediction and estimation

4. Control

1. Data description

Engineers and scientists frequently use equations to summarize or describe a set of data. Regression analysis is helpful in developing such equations. For example, we may collect a considerable amount of delivery time and delivery volume data, and a regression model would probably be a much more convenient and useful summary of those data than a table or even a graph

2. Parameter estimation

Sometimes parameter estimation problems can be solved by regression methods. For example, chemical engineers use the Michaelis – Menten equation

Y =β1x /( x+β2 ) +ε to describe the relationship between the velocity of reaction y

And concentration x.  Now in this model, β1 is the asymptotic velocity of the reaction, that is, the maximum velocity as the concentration gets large. If a sample of observed values of velocity at different concentrations is available, then the engineer can use regression analysis to fit this model to the data, producing an estimate of the maximum velocity.

3. Prediction and estimation

Many applications of regression involve prediction of the response variable. For example, we may wish to predict delivery time for a specified number of cases of soft drinks to be delivered. These predictions may be helpful in planning delivery activities such as routing and scheduling or in evaluating the productivity of delivery operations. The dangers of extrapolation when using a regression model for prediction because of model. However, even when the model form is correct, poor estimates of the model parameters may still cause poor prediction performance.

4. Control

Regression models may be used for control purposes. For example, a chemical engineer could use regression analysis to develop a model relating the tensile strength of paper to the hardwood concentration in the pulp. This equation could then be used to control the strength to suitable values by varying the level of hard-wood concentration. When a regression equation is used for control purposes, it is important that the variables be related in a causal manner.

Regression analysis is helpful statistical method that can be leveraged across an organization to determine the degree to which particular independent variables are influencing dependent variables. 

The possible scenarios for conducting regression analysis to yield valuable, actionable business insights are endless.

11. Question: Define precision and accuracy?

Solution:

Precision refers to the amount of scatter in a set of numbers presumed to measure the same quantity. For example, suppose you repeatedly placed the same coin on an analytical balance. The scatter in your results would define the precision of the measurement. Accuracy refers to the degree to which the set of numbers represents the "true" value of the quantity. If, in the above example, the balance were not properly levelled, it might give good precision, but the value could be wrong, thereby leading to poor accuracy.

Further, there is important aspect of reporting measurement. It should be consistent, systematic and revealing in the context of accuracy and precision.

Accuracy is a measure of how close the result of the measurement comes to the "true", "actual", or "accepted" value. It is associated with systematic error.

Precision of measurement is related to the ability of an instrument to measure values in greater details. The precision of a measuring instrument is determined by the smallest unit to which it can measure. The precision is said to be the same as the smallest fractional or decimal division on the scale of the measuring instrument. It is associated with random error.

Accuracy of a measurement is how close the measured value is to the true value.

Example Suppose you weigh a box and noted 3.1 kg but its known value is 9 kg, then your measurement is not accurate.

Precision is the resolution or closeness of a series of measurements of a same quantity under similar conditions.

Suppose you weigh the same box five times and get close results like 3.1, 3.2, 3.22, 3.4, and 3.0 then your measurements are precise.

Let us take a look on another example for clarity. If the true value of a certain length is 3.678 cm and two instruments with different resolutions, up to 1 (less precise) and 2 (more precise) decimal places respectively are used. If first measures the length as 3.5 and the second as 3.38 then the first has more accuracy but less precision while the second has less accuracy and more precision.

Accuracy and Precision are two independent terms. You can be very accurate but non-precise, or vice-versa.

Measurements of units revolve around accuracy and precision, that’s why we find our experiment readings to be in decimal form.
 

12. Question: Discuss absolute error, relative error?

Solution:

Absolute Error

Let the values obtained in several measurements are  a1 , a2  , a3……..an The arithmetic mean of these values is taken as the best possible value of the quantity under the given conditions of measurement as a mean  = (a1 + a2  + a3  … + an )/n

The magnitude of the difference between the true value of the quantity and the individual measurement value is called the absolute error of the measurement.

This is denoted by |Δa|.

Note: In the absence of any other method of knowing true value, we considered arithmetic mean as the true value.

Then the errors in the individual measurement values are

Δa1  =  amean  – a1

Δa2 =  amean – a2

.... .... ....

.... .... ....

Δan  = amean  – an

The Δa calculated above may be positive in certain cases and negative in  Some other cases. But absolute error |Δa| will always be positive.

 Mean Absolute Error

It is the arithmetic mean of the magnitude of absolute errors in all the measurement of the quantity. It is generally represented by Δamean. If we do a single measurement, the value we get may be in the range  amean ± Δamean

So a = amean ± Δamean

Relative Error

The relative error is the ratio of the mean absolute error Δamean  to the

Mean value amean  of the quantity measured.

i.e., Relative error = Δamean / a mean

13. Question: Discuss percentage error in detail?

Solution:

Percentage error,

 δa = (Δamean /amean ) × 100%

Combination of Errors

(a) Error of a sum or a difference

When two quantities are added or subtracted, the absolute error in the  final result is the sum of the absolute errors in the individual quantities.

Z = A + B

We have by addition, Z ± ΔZ = (A ± ΔA) + (B ± ΔB).

The maximum possible error in Z

ΔZ = ΔA + ΔB

For the difference Z = A – B, we have

Z ± Δ Z = (A ± ΔA) – (B ± ΔB) = (A – B) ± ΔA ± ΔB

Or, ± ΔZ = ± ΔA ± ΔB

The maximum value of the error ΔZ is again ΔA + ΔB.

(b) Error of a product or a quotient

When two quantities are multiplied or divided, the relative error in the result is the sum of the relative errors in the multipliers.

Suppose Z = AB and the measured values of A and B are A ± ΔA and B ±ΔB. Then

Z ± ΔZ = (A ± ΔA) (B ± ΔB) = AB ± B ΔA ± A ΔB ± ΔA ΔB.

Dividing LHS by Z and RHS by AB we have,

1 ± (ΔZ/Z) = 1 ± (ΔA/A) ± (ΔB/B) ± (ΔA/A)(ΔB/B).

Since ΔA and ΔB are small, we shall ignore their product.

Hence the maximum relative error

ΔZ/ Z = (ΔA/A) + (ΔB/B).

(c) Error in case of a measured quantity raised to a power

The relative error in a physical quantity raised to the power k is the k times the relative error in the individual quantity.

Suppose Z = A2   Then,

ΔZ/Z = (ΔA/A) + (ΔA/A) = 2 (ΔA/A).

Hence, the relative error in A2  is two times the error in A.

In general, if Z = (Ap Bq )/Cr

Then,

ΔZ/Z = p (ΔA/A) + q (ΔB/B) + r (ΔC/C).

14. Question: What are types of Errors?

Solution:

The errors in measurement can be broadly classified as

1. Systematic errors
2. Random errors
3. Least count error

1. Systematic Errors

The systematic errors are those errors that tend to be in one direction, either positive or negative. Basically, these are the errors whose causes are known.

a)     Instrumental Errors

These errors arise from the errors due to imperfect design or calibration of the measuring instrument, zero error in the instrument etc.

Example: Temperature graduations of a thermometer may be inadequately calibrated. It may read 103 °C at the boiling point of water at STP whereas it should read 100 °C.

In a vernier calliper the zero mark of vernier scale may not coincide with the zero mark of the main scale

b)    Imperfection in experimental technique or procedure

To determine the temperature of a human body, a thermometer placed under the armpit will always give a temperature lower than the actual value of the body temperature.

Other external conditions such as changes in humidity, temperature, wind velocity, etc. during the experiment may systematically affect the measurement.

c)     Personal errors

Such errors arise due to an individual’s bias, lack of proper setting of the apparatus or individual’s carelessness in taking observations without observing proper precautions, etc.

For example, if you, by habit, always hold your head a bit too far to the right while reading the position of a needle on the scale, you will introduce an error due to parallax.

2.     Random Errors

The random errors are those errors, which occur irregularly and hence are random with respect to sign and size. These can arise due to random and unpredictable fluctuations in experimental conditions (e.g. Unpredictable fluctuations in temperature, voltage supply, mechanical vibrations of experimental set-ups, etc.), personal (unbiased) errors by the observer taking readings, etc.

For example, when the same person repeats the same observation, it is very likely that he may get different readings every time.

3.     Least Count Error

Least count is the smallest value that can be measured by the measuring instrument. Least count error is the error associated with the resolution of the instrument.

For example, a vernier callipers has the least count as 0.01 cm; a spherometer may have a least count of 0.001 cm.

Least count error belongs to the category of random errors but within a limited size; it occurs with both systematic and random errors.

15. Question: Difference between Uncertainty and error?

Solution:

Uncertainty is a quantification of the doubt about the measurement result.

Or

Uncertainty means the range of possible values within which the true value of the measurement lies.

When you repeat a measurement you often get different results. There is an uncertainty in the measurement that you have taken. It is important to be able to determine the uncertainty in measurements so that its effect can be taken into consideration when drawing conclusions about experimental results.

Error means the difference between a measured value and the true value for a measurement.