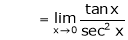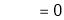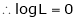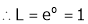Unit – 1
Higher order derivatives and applications
Q 1. Compute limx→−2(3x2+5x−9)
Solution:
First, use property 2 to divide the limit into three separate limits. Then use property 1 to bring the constants out of the first two. This gives,
Limx→−2(3x2+5x−9) =limx→−2(3x2) + limx→−2(5x) −limx→−2(9)
=3(−2)2+5(−2) −(9)
= -7
Q 2. Find the limits of limx→3 [x(x+2)].
Solution: limx→3 [x(x+2)] = 3(3+2) = 3 x 5 = 15
Q 3: Differentiability Implies Continuity If f is differentiable at x0, then f is continuous at x0.
It turns out that equation (1) can be restated.
Definition. Derivatives in One Dimension - Alternate Definition
Solution: Let f : D ⊂ R → R and let x0 be an interior point of D.
Then f is differentiable at x0 if there is a number f ′ (x0) such that (2) lim x→x0 f(x) − f(x0) − (x − x0)f ′ (x0) |x − x0| = 0 and the number f ′ (x0) is called the derivative of f at x0.
We use this definition to create a definition of the derivative for functions of
Several variables. Definition. Derivatives in Higher Dimensions Let f : D ⊂ R n → R
And let P0 be an interior point of D. Then f is differentiable at P0 if there is a vector
f ′ (P0) such that
 lim P→P0 f (P) − f (P0) − # » P0P · f ′ (P0) =0
lim P→P0 f (P) − f (P0) − # » P0P · f ′ (P0) =0
|P − P0|
Q 4:Suppose there is a c∈Rc∈R and a function E:R→RE:R→R, s.t. f(x)=f(a)+c(x−a)+E(x)f(x)=f(a)+c(x−a)+E(x) near aa and limx→aE(x)x−a=0limx→aE(x)x−a=0.
Then:
Limx→af(x)−f(a)x−a−c=limx→af(x)−f(a)−c(x−a)x−a=0limx→af(x)−f(a)x−a−c=limx→af(x)−f(a)−c(x−a)x−a=0
So that means:
f′(x)f′(x) exists and f′(x)=cf′(x)=c. Of course writing f′(x)f′(x) instead of cc before you know this is indeed begging the question.
Q 5: For a function f: R→R f: R→R, suppose that there exist a real number AA such that for all xx in some neighbourhood of aa,
f(x)=f(a)+A(x−a) +E(x)f(x)=f(a)+A(x−a) + E(x)
And that
Limx → aE(x)(x−a) =0limx→aE(x)(x−a) =0
We say that ff is differentiable at aa. If ff is differentiable at aa we define f′(a)f′(a) by
f′(a)=Af′(a)=A
This definition is not circular and is useful since it can be generalized to the case where f: Rn→Rm f: Rn→Rm. In this case AA is a matrix instead of a real number (to be precise, AA is a linear operator
Q 6: Find the nth derivative of sin3 x
Solution: we know that sin 3x= 3sin x 4sin3 x = sin3x= 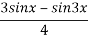
Differentiate n times w.r.t x,
 (sin3 x) =
(sin3 x) = 
 (3 sinx- sin3x)
(3 sinx- sin3x)
= ( -3n. Sin (3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
( -3n. Sin (3x+ nπ/2) + 3 sin (x+ nπ/2)) nϵz
Q 7: Find the nth derivative of sin 5x. Sin 3x.?
Solution: let y = sin 5x.sin 3x=  ( sin 5x.sin 3x)
( sin 5x.sin 3x)
⇒y=  ( cos 2x -cos8x)
( cos 2x -cos8x)
⇒ y= (cos 2x- cos8x)
(cos 2x- cos8x)
Differentiate n times w.r.t x,
Yn = 
 (cos 2x - cos8x)
(cos 2x - cos8x)
⇒ yn =  ( 2 n (cos (2x+ nπ/2)- 8n.cos (8x + nπ/2)) nϵz.
( 2 n (cos (2x+ nπ/2)- 8n.cos (8x + nπ/2)) nϵz.
Q 8: Successive n th derivative of nth elementary function ie., exponential
If y = ae n x + be –nx,then show that y2= n2y
Solution: Y= aenx + be-nx
y 1 = a.n.enx - b.n.e-nx
y2 = an2enx – bn2 e-nx = n2 (ae nx+ be –nx)
y2= n2y.
Q 9: If y= e-kx/2(a cosnx+ b sinnx) then show that., y2+ ky1+(n2+ k2/4) y =0
Solution: y= e-kx/2(a cosnx+ b sinnx)
Differentiating w.r.to. x.,
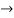 Y1 = e-kx/2(-an sin nx + bn cos nx) - k/2. y
Y1 = e-kx/2(-an sin nx + bn cos nx) - k/2. y
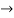 Y1+ k/2. y = ne-kx/2 (-an sin nx + bn cos nx)
Y1+ k/2. y = ne-kx/2 (-an sin nx + bn cos nx) 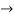 (1)
(1)
Differentiating w.r.to x.,
Y2+ k/2. y1 = ne-kx/2 (-k/2) ( -an sin nx + bn cos nx) + n e-kx/2(-an cosnx- bn sinnx).
= -(k/2) (y1+ k/2 y)- n2 y = - (k/2 y1)- (k2/4) y- n2y.
 y2 + ky1 +(n2+ k2/4) y = 0.
y2 + ky1 +(n2+ k2/4) y = 0.
Q 10: If Y 2) = log (x +
2) = log (x +  2)) then show that
2)) then show that
(1 + x 2) y1 +x y =1
Solution: Y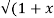 2) = log (x +
2) = log (x + 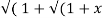 2))
2))
Differentiating w.r.to x.,
y.1/ 2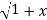 2 .2x+
2 .2x+ 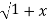 2. Y1.
2. Y1.
= (1+x) y + x y = 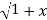 . 1/x
. 1/x 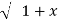 2 .
2 .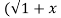 2) +x/
2) +x/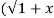 2 =1
2 =1
Q 11: If Y 2) = log (x +
2) = log (x +  2)) then show that
2)) then show that
(1 + x 2) y1 + x y =1
Solution: Y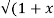 2) = log (x +
2) = log (x +  2))
2))
Differentiating w.r.to x.,
y.1/ 2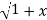 2 .2x+
2 .2x+  2. Y1.
2. Y1.
= (1+x y +x y = 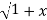 . 1/x+
. 1/x+ 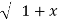 2 .
2 .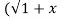 2) +x/
2) +x/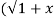 2 =1
2 =1
Q 12:Evaluate 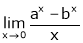
Solution:
Let
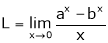 …
… 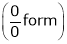
 By L – Hospital rule,
By L – Hospital rule,
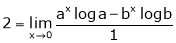

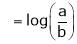
Q 13: Evaluate 
Solution:
Let
 …
… 
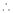 By L – Hospital rule
By L – Hospital rule
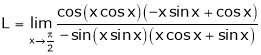
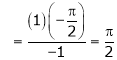
Q 14: Evaluate 
Solution:
Let
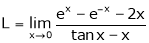 …
… 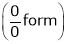
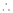 By L – Hospital rule
By L – Hospital rule
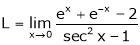 …
… 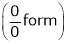
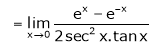 …
… 

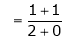


Q 15: Find the value of a, b if 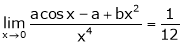
Solution:
Let
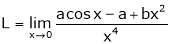 …
… 
 By L – Hospital rule
By L – Hospital rule
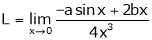 …
… 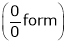
 …
… 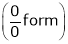
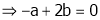 … (1)
… (1)
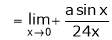 …
… 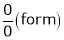
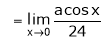
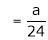
But 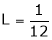
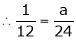
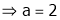
 From equation (1)
From equation (1)

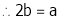

Q 16: Evaluate 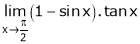
Solution:
Let
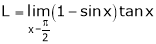 …
… 
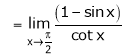 …
… 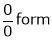
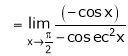 (By L – Hospital Rule)
(By L – Hospital Rule)
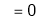
Q 17: Evaluate 
Solution:
Let
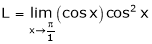 … 0o form
… 0o form
Taking log on both sides we get,
 …
… 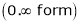
 …
… 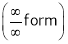
 By L – Hospital Rule
By L – Hospital Rule
i.e. 
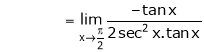
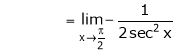

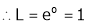

Q 18: Evaluate 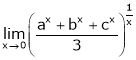
Solution:
Let
 …
… 
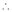 Taking log on both sides,
Taking log on both sides,
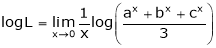
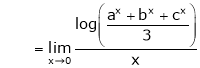 …
… 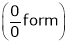
 By L – Hospital rule,
By L – Hospital rule,

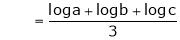
i.e. 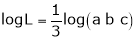

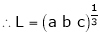
Q 19: Evaluate 
Solution:
Let
 …
… 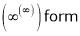
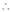 Taking log on both sides, we get
Taking log on both sides, we get

 …
… 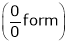
 By L – Hospital Rule,
By L – Hospital Rule,