Unit – 5
Unit – 5
Algebra of Complex numbers and Roots of polynomial Equations
Q 1: Simplify 16 i+10i (3-i)
Solution:
Given,
16i +10i (3-i)
=16i+10i(3i) +10i(-i)
=16i+30i-10i2
=46i-10(-1)
=46i+10
Here real part is 10 and imaginary part is 46
Q 2: Express the following into a+ib form
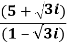
Solution:
Given., 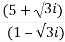
z = 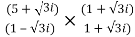 =
=  =
= +
+ i
i
Modulus, 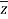 =
= 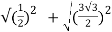 =
=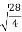 =
= 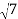
Conjugate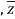 = (
= (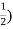 -
- 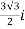
Q 3: Find the polar form of 7-5j
Solution:
We need to find r and 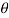
r=
=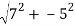
= 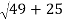
= 8.6
8.6
To find θ, we first find the acute angle α ,
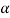 = tan-1(
= tan-1( )
)
= tan-1( )
)
= 35.540
7-5j is in the fourth quadrant so we we have,
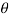 = 3600 -35.540 = 324.460
= 3600 -35.540 = 324.460
So, expressing 7-5j in the polar form as.,
7-5j = 8.6(cos324.50 +j sin324.50)
Q 4: Represent 1+j in polar form
in polar form
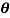 = arctan
= arctan 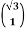 =600
=600
Solution: R= 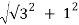 =
= 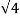 =2
=2
So,
1+j = 2
= 2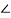 600 = 2(cos600 +jsin 600)
600 = 2(cos600 +jsin 600)
Q 5: Write (  ) 7 in the form of a+ib
) 7 in the form of a+ib
First determine the radius ie., r
Solution: Let r= 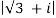
r = 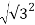 + i2
+ i2
r= 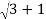
r=2
Now cos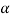 =-
=-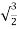 and sin
and sin 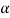 =
= ,
, 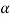 must be in the first quadrant and
must be in the first quadrant and  =300
=300
Therefore,
( 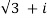 ) 7 =
) 7 = 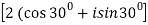 7
7
(  ) 7 = 27 [cos 7.300 +i sin 7.300]
) 7 = 27 [cos 7.300 +i sin 7.300]
= 128[cos 2100+isin2100]
= 28 +i
+i 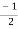
( 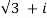 ) 7 = 64
) 7 = 64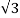 -64 i
-64 i
Q 6: Write ( +i
+i  )4 in the form of a+ib
)4 in the form of a+ib
Solution: First, we determine the radius,
r = 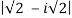
r= 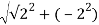
r=
r=2
Now,
(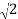 +i
+i 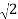 )4 =
)4 =  4
4
= [24 (cos 4.3150 + isin 4.3150)
=16(cos 21600+i sin 21600)
= 16( cos 1800+i.sin 1800)
= 16(-1+0i)
= -16
Q 7: Prove that function 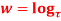 is analytic function.
is analytic function.
Solution: Real and Imaginary parts of 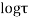 are
are
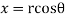
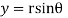
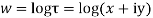
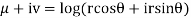


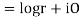

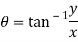
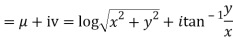
If, 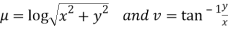
On differentiating u,v we get
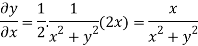
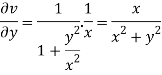
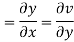
Again differentiating
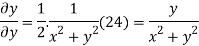
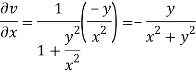
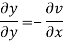
Hence e-R-Equation satisfies.
Q 8: 2y=4x−16 and y=2x−8 perpendicular.
Solution: Let 2y =4x-16  (1)
(1)
Y=2x-8  (2)
(2)
Let s write equation (1) in the form of y= mx+c and  2)
2)
 y= 2x-8 and y = 2x-8
y= 2x-8 and y = 2x-8
Here we see that there is only one line,
But if there are two lines, they would have been parallel as the gradients are same.
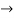 y= 2x+5 and y= 2x-8 are parallel
y= 2x+5 and y= 2x-8 are parallel
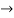 y= --
y= -- x-8 and y=2x-8 are perpendicular
x-8 and y=2x-8 are perpendicular
--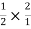 are perpendicular.
are perpendicular.
Q 9: Lisa will make up a punch that is 25% fruit juice by adding pure fruit-juice to a
2-liter mixture that is 10% pure fruit-juice. How many litres of pure fruit juice does she need to add?
Solution:
Let’s call the amount to be found z
Then you will end up with x+2L of 25% juice
This will contain 0.25(x+2) =0.25x+0.5pure juice
The original 2L already contained 0.10.2=0.2 juice
So we added 0.25x=0.3 juice, but this is also x(as x=100% juice).
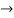 0.25x+0.3=x
0.25x+0.3=x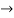 0.75x=0.3
0.75x=0.3 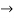 x=0.4 liter
x=0.4 liter
Q10: Finding the real root of the following polynomial equation using cardano’s method
X3+2x2+3x+4=0
Solution: Given that., a=1, b=2, c=3, d=4
Compute Q and R:
Q=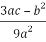 =
= 
R= 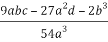 =
=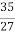
Compute S and T :
S=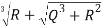 =
= 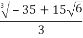
T= 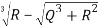 =
= 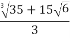
Compute the roots:
X1 = S+T- 
= 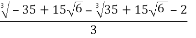
= -1.651
X2 = 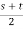 -
- +i
+i (s-t)
(s-t)
= + i.
+ i.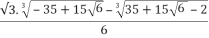
X3 =  -
-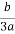 +i
+i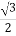 (s-t)
(s-t)
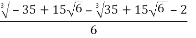 - i.
- i.
 -0.175 -1.547 i.
-0.175 -1.547 i.
Given quadratic equation: 36x4 -72x3-391x2-123x+270
Applying Ferrari’s method:
We have,
A=36, B=-72, C=-391, D=-123, E=270

 -
- 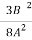 =-
=- 
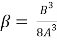 -
-  +
+ = -
= -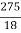
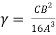 -
- -
-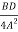 +
+ =
= 
P= - 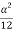 –
–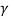 =
=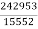 =15.62
=15.62 16
16
Q=  -
- 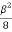 -
- = -
= - 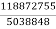 =23.59
=23.59 24
24
Finally,
R= -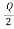
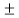
 = -
= -

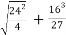
By solving the above equation, we get., 12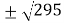 .
.
Q 11: Consider the quadratic equation y4+ay3+by2+cy+d=0
Solution: By substituting y= x- the above equation will be reduced to the following
the above equation will be reduced to the following
=X4+ px2+qz+r=0, (1)
(1)
The above equation doesn’t contain x3., if one introduces an auxiliary parameter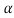 ,then the left hand side of equation (1) can be written as follows:
,then the left hand side of equation (1) can be written as follows:
=X4+ px2+qz+r = (x2 +  +
+ )2 – [2ax2 –qx+(
)2 – [2ax2 –qx+( 2 +p
2 +p +
+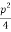 -r)]
-r)] (2)
(2)
= q2 -4.2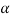 (
(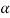 2 +p
2 +p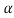 +
+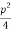 –r) =0
–r) =0
Then the required equation for 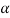 =
=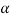 0 the polynomial in square brackets in equation (2) has one double root
0 the polynomial in square brackets in equation (2) has one double root
X0= 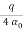
Unit – 5
Algebra of Complex numbers and Roots of polynomial Equations
Q 1: Simplify 16 i+10i (3-i)
Solution:
Given,
16i +10i (3-i)
=16i+10i(3i) +10i(-i)
=16i+30i-10i2
=46i-10(-1)
=46i+10
Here real part is 10 and imaginary part is 46
Q 2: Express the following into a+ib form
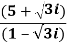
Solution:
Given., 
z =  =
= 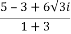 =
= +
+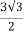 i
i
Modulus, 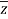 =
=  =
=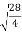 =
= 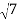
Conjugate = (
= (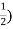 -
- 
Q 3: Find the polar form of 7-5j
Solution:
We need to find r and 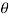
r=
=
= 
= 8.6
8.6
To find θ, we first find the acute angle α ,
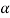 = tan-1(
= tan-1( )
)
= tan-1( )
)
= 35.540
7-5j is in the fourth quadrant so we we have,
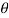 = 3600 -35.540 = 324.460
= 3600 -35.540 = 324.460
So, expressing 7-5j in the polar form as.,
7-5j = 8.6(cos324.50 +j sin324.50)
Q 4: Represent 1+j in polar form
in polar form
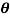 = arctan
= arctan  =600
=600
Solution: R=  =
= 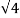 =2
=2
So,
1+j = 2
= 2 600 = 2(cos600 +jsin 600)
600 = 2(cos600 +jsin 600)
Q 5: Write (  ) 7 in the form of a+ib
) 7 in the form of a+ib
First determine the radius ie., r
Solution: Let r= 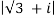
r = 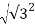 + i2
+ i2
r= 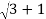
r=2
Now cos =-
=-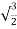 and sin
and sin 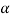 =
= ,
,  must be in the first quadrant and
must be in the first quadrant and 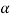 =300
=300
Therefore,
( 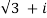 ) 7 =
) 7 = 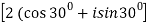 7
7
(  ) 7 = 27 [cos 7.300 +i sin 7.300]
) 7 = 27 [cos 7.300 +i sin 7.300]
= 128[cos 2100+isin2100]
= 28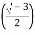 +i
+i 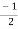
(  ) 7 = 64
) 7 = 64 -64 i
-64 i
Q 6: Write ( +i
+i  )4 in the form of a+ib
)4 in the form of a+ib
Solution: First, we determine the radius,
r = 
r= 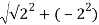
r=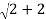
r=2
Now,
(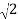 +i
+i 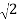 )4 =
)4 = 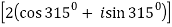 4
4
= [24 (cos 4.3150 + isin 4.3150)
=16(cos 21600+i sin 21600)
= 16( cos 1800+i.sin 1800)
= 16(-1+0i)
= -16
Q 7: Prove that function 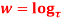 is analytic function.
is analytic function.
Solution: Real and Imaginary parts of  are
are
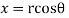
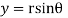
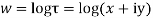
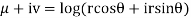
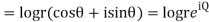
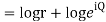
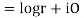
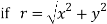
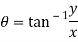
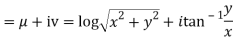
If, 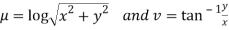
On differentiating u,v we get
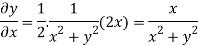
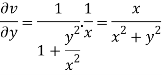
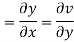
Again differentiating
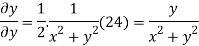
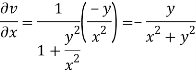
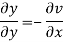
Hence e-R-Equation satisfies.
Q 8: 2y=4x−16 and y=2x−8 perpendicular.
Solution: Let 2y =4x-16 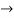 (1)
(1)
Y=2x-8 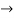 (2)
(2)
Let s write equation (1) in the form of y= mx+c and 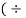 2)
2)
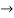 y= 2x-8 and y = 2x-8
y= 2x-8 and y = 2x-8
Here we see that there is only one line,
But if there are two lines, they would have been parallel as the gradients are same.
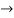 y= 2x+5 and y= 2x-8 are parallel
y= 2x+5 and y= 2x-8 are parallel
 y= --
y= -- x-8 and y=2x-8 are perpendicular
x-8 and y=2x-8 are perpendicular
-- are perpendicular.
are perpendicular.
Q 9: Lisa will make up a punch that is 25% fruit juice by adding pure fruit-juice to a
2-liter mixture that is 10% pure fruit-juice. How many litres of pure fruit juice does she need to add?
Solution:
Let’s call the amount to be found z
Then you will end up with x+2L of 25% juice
This will contain 0.25(x+2) =0.25x+0.5pure juice
The original 2L already contained 0.10.2=0.2 juice
So we added 0.25x=0.3 juice, but this is also x(as x=100% juice).
 0.25x+0.3=x
0.25x+0.3=x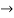 0.75x=0.3
0.75x=0.3 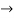 x=0.4 liter
x=0.4 liter
Q10: Finding the real root of the following polynomial equation using cardano’s method
X3+2x2+3x+4=0
Solution: Given that., a=1, b=2, c=3, d=4
Compute Q and R:
Q=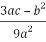 =
= 
R=  =
=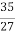
Compute S and T :
S=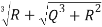 =
= 
T= 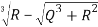 =
= 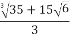
Compute the roots:
X1 = S+T- 
= 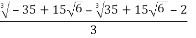
= -1.651
X2 = 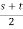 -
-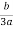 +i
+i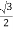 (s-t)
(s-t)
=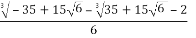 + i.
+ i.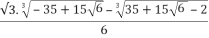
X3 = 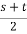 -
-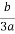 +i
+i (s-t)
(s-t)
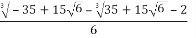 - i.
- i.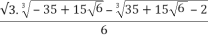
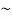 -0.175 -1.547 i.
-0.175 -1.547 i.
Given quadratic equation: 36x4 -72x3-391x2-123x+270
Applying Ferrari’s method:
We have,
A=36, B=-72, C=-391, D=-123, E=270

 -
- 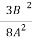 =-
=- 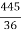
 -
- 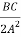 +
+ = -
= -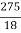
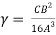 -
- -
-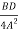 +
+ =
= 
P= -  –
–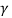 =
=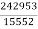 =15.62
=15.62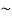 16
16
Q=  -
- 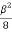 -
-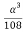 = -
= -  =23.59
=23.59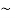 24
24
Finally,
R= -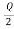
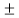
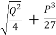 = -
= -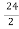

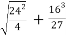
By solving the above equation, we get., 12 .
.
Q 11: Consider the quadratic equation y4+ay3+by2+cy+d=0
Solution: By substituting y= x- the above equation will be reduced to the following
the above equation will be reduced to the following
=X4+ px2+qz+r=0, (1)
(1)
The above equation doesn’t contain x3., if one introduces an auxiliary parameter ,then the left hand side of equation (1) can be written as follows:
,then the left hand side of equation (1) can be written as follows:
=X4+ px2+qz+r = (x2 +  +
+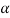 )2 – [2ax2 –qx+(
)2 – [2ax2 –qx+(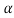 2 +p
2 +p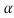 +
+ -r)]
-r)] (2)
(2)
= q2 -4.2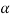 (
(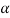 2 +p
2 +p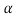 +
+ –r) =0
–r) =0
Then the required equation for 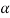 =
=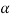 0 the polynomial in square brackets in equation (2) has one double root
0 the polynomial in square brackets in equation (2) has one double root
X0= 