Unit – 3

Applications of Partial differentiation

Q 1:   Find the equation of the tangent to the curve 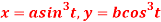at the point ?

Solution: Given Curve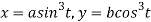 

Differentiating both side with respect to t.

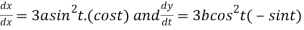
By Chain Rule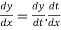 

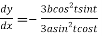
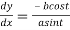
Therefore, the equation of the tangent

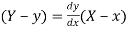
                     Or   …(i)

At the point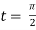  

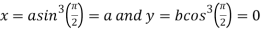
Also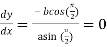  

Substituting all these values in (i) we get

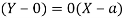
Hence the equation of the tangent is .

Q 2:  At what point is the tangent to the curve parallel to the chord joining the points (0,0) and (0,1).

Solution: Given curve is

Equation of the chord joining the points (0,0) and (0,1) is

       Or 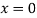i.e.  Parallel toY-axis    …(i)

Given curve is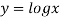

                         Differentiating both side with respect to x.

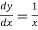
           Equation of tangent parallel to Y-axis is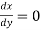  

                                             Or 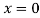   (as above) 

Since curve is

     At    (ii)

From (i) and (ii) we conclude that the point tangent parallel to the chord is .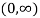

       Hence the point tangent parallel to the chord is .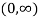

Q 3: Prove that 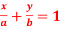touches the curve at the point where the curve crosses the axis of y.

Solution: Given curve is

It will cross the y-axis at x=0, we get

Hence the point of the curve on the Y-axis is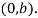

Since curve is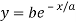

Differentiating both side with respect to x, we get

                         .

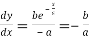
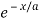At point (0, b) we have 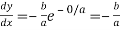    …(i)

Again given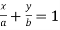

   Differentiating both side with respect to x, we get

Again at the point (0, b) we have 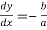…..(ii)

As we know that two curve touches each other then they have Same Lope at the point of intersection.

From (i) and (ii) we conclude that both the curve touches each other on Y-axis.

Q 4: Find the equation of the normal of the curve 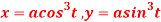at.

Solution: Given curve 

Differentiating both side with respect to t.

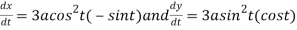
   By Chain Rule

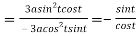
At the point ,

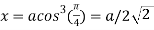
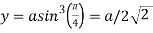
Also

Therefore, equation of the normal at

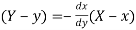
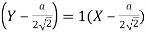
Hence the equation of the normal at .

Q 5: Prove that the curve 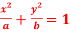and  will cut orthogonally if ?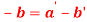

Solution: Given curves 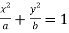     …(i)

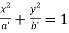And       …(ii)

Let 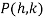   be a intersection point of curve (i) and (ii)

Then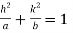 

    And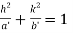 

      On solving we get

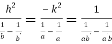
       Or    …(iii)

    Differentiating (i) with respect to x.

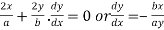
   At the point slope of (i) is given by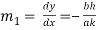

     Differentiating (ii) with respect to x.

   At the point slope of (ii) is given by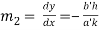

      For orthogonal intersection, we have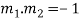

     Substituting the values of slopes we get,

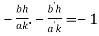
                  Or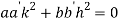

Putting values from (iii) we get

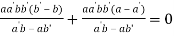
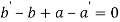
               Or

Hence proved.

Q 6: Find the lengths of the tangent, normal, sub tangent and subnormal for the cycloid:

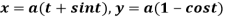
Solution: The equation of the cycloid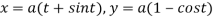

     Differentiating both with respect to t .

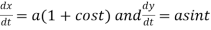
By Chain Rule

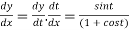
Length of tangent is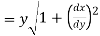

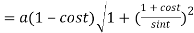
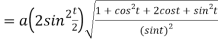
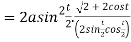
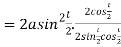
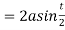
Length of normal is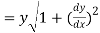

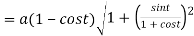
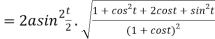
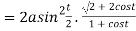
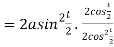
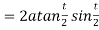
Length of sub tangent =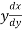

                                        =

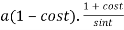
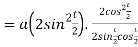
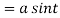
Length of sub normal =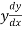

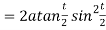
Q 7: Find out the maxima and minima of the function

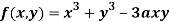
  Solution: Given 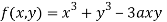    …(i)

         Partially differentiating (i) with respect to x we get

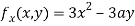                   ….(ii)

         Partially differentiating (i) with respect to y we get

                    ….(iii)

          Now, form the equations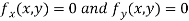

                    Using (ii) and (iii) we get

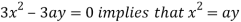
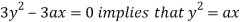
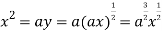                                  using above two equations

                     Squaring both side we get

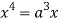
                      Or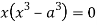 

                       This show that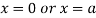

                         Also we get

                 Thus we get the pair of value as

                  Now, we calculate

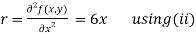
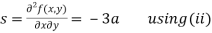
      Putting above values in

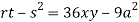
      At point (0,0) we get

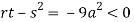
      So, the point (0,0) is a saddle point.

      At point 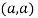we get

        So the point 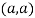is the minimum point where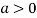

          In case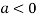 

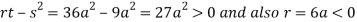
         So the point 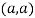is the maximum point where

Q 8: Find the maximum and minimum point of the function

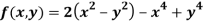
      Solution: Partially differentiating given equation with respect to and x and y then equate them to zero                 

       On solving above we get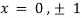 

         Also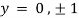

            Thus, we get the pair of values (0,0), (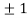,0) and (0,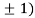

        Now, we calculate

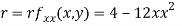
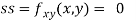
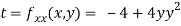
        At the point (0,0)

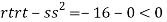
       So function has saddle point at (0,0).

       At the point (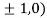

         So the function has maxima at this point (.

        At the point (0,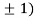

       So the function has minima at this point (0,.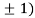

        At the point (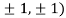

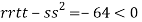
        So the function has an saddle point at (

Q 9: Divide 24 into three parts such that the continued product of the first, square of second and cube of third may be maximum.                                    

Solution: Let first number be x, second be y and third be z.

According to the question

Let the given function be f

And the relation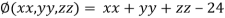

By Lagrange’s Method

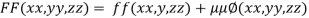
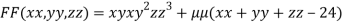        ….(i)

Partially differentiating (i) with respect to x,y and z and  equate  them  to zero

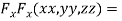
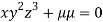     ….(ii)

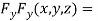
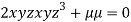      ….(iii)

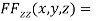
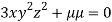      ….(iv)

  From (ii),(iii)  and (iv) we get

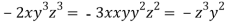
On solving

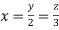
Putting it in given relation we get

             Or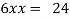 

            Or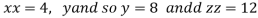

Thus, the first number is 4 second is 8 and third is 12

Q 10: The temperature T at any point   in space is  .Find  the highest temperature on the surface of the unit sphere.

Solution: Given function is  

On the surface of unit sphere given   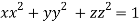  [ is an equation of unit sphere in 3   dimensional space]

By Lagrange’s Method

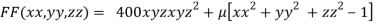           ….(i)

Partially differentiating (i) with respect to  x, y and z and equate them to zero

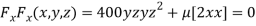  or           …(ii)

  or           …(iii)

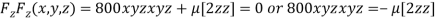            …(iv)

Dividing (ii) and (ii) by (iv) we get

Using given relation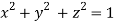 

                         Or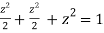       

                         Or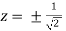               

So that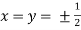

         Or 

Thus, points are

The maximum temperature is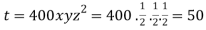

Q 11: If ,Find the value of x and y for which is maximum.

Solution: Given function is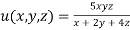

And relation is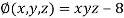

By Lagrange’s Method

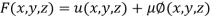
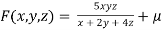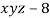      []    ..(i)

Partially differentiating (i) with respect to  x, y and z and equate them to zero

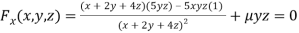
                 Or 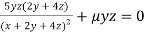      …(ii)

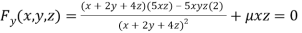
                   Or 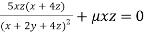      …(iii)

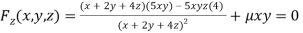
                   Or 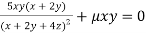      …(iv)

On solving (ii),(iii) and (iv) we  get

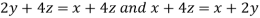
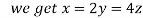
Using the given relation  we get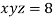

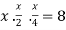
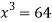
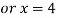
So that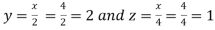

Thus, the point for the maximum value of the given function is

Q 12: Find the points on the surface 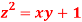nearest to the origin.

Solution: Let 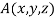be any point on the surface, then its distance from the origin 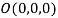is

Thus, the given equation will be

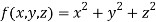
And relation is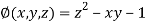

By Lagrange’s Method

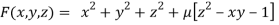           ….(i)

Partially differentiating (i) with respect to  x, y and z and equate them to zero

               Or 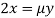       …(ii)

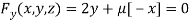
               Or 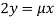       …(iii)

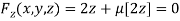
                   Or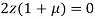

                      Or

On solving equation (ii) by (iii) we get

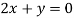
And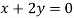     

On subtracting we get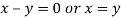

Putting in above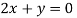

                           Or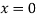 

Thus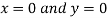

Using the given relation, we get

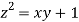  = 0.0 +1=1

Or 

Thus, point on the surface nearest to the origin is