Unit – 6
Infinite Series
Q 1: Identify the sequence of the following function n (n+3)
- 4, 10, 26, …
- 4, 12, 18, …
- 2, 10, 16, …
- 4, 10, 27, …
Solution: Correct option is A. The given function is n(n+3),
When n = 1, 1(1+3) = 4
n = 2, 2(2+3) = 10
n=3, 3(3+3) = 27
So, 4, 10, 27…is the function for the sequence n(n+3).
Q 2: Question: Adding first 100 terms in a sequence is
- Term
- Series
- Constant
- Sequence
Solution: Correct option is B. Adding first 100 terms in a sequence is series. Also adding the number of some set is a series.
Q 3: Determine whether the following series converges or diverges
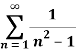
Solution:
Consider the given series ie., 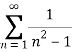

 =
=  =
= -
- -
-
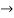
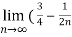 -
-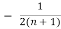 ) =
) = 
Since,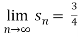
 therefore the given series is convergent.
therefore the given series is convergent.
Q 4: Determine whether the following series is divergent or convergent
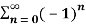
Solution: Given,
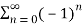
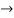 s0 =1
s0 =1
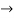 s1 = 1-1=0
s1 = 1-1=0
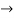 s2 = 1-1+1=1
s2 = 1-1+1=1
 s3 = 1-1+1-1=0
s3 = 1-1+1-1=0
Hence the series diverges since 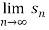 doesn’t exist.
doesn’t exist.
Q 5: 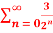
Solution: Given  =
=  n
n
= 3(1) +3( ) +3(
) +3( )2 +.........
)2 +.........
Has a ratio of r=  with a=3
with a=3
As 0< 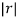 <1, the series converges and the sum is
<1, the series converges and the sum is
S=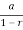 =
=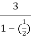 =6.
=6.
Q 6: Solve the following geometric series,
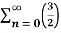 n =1+
n =1+  +
+ +
+ +........
+........
Solution: Gives a ratio of r=
Because 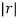
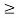 1, the series diverges.
1, the series diverges.
Q 7:  =
= 
Solution: Here p = 3 so p>1, thus the given series converges.
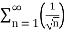 =
= 
Here p= ie., p<1, thus the given series diverges
ie., p<1, thus the given series diverges
Q 8: 
Solution:  +
+
= -3. +5.
+5.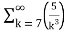
=-3. +5.
+5.
Therefore., here p=2 ,3 ie., p>1
Hence the given series converges.
Q 9: Find whether the following series is convergent or divergent?
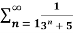
Solution:
= 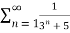 <
<  =
= 
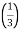 n-1 <
n-1 <
So the series converges
Q 10: 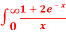 . Dx., test for convergence
. Dx., test for convergence
Solution:
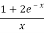 >
> 
Hence the series diverges
Ratio test:
To test convergence of ratio test we follow the below method,
Consider,
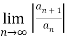 = L
= L
If L<1  is absolutely convergent
is absolutely convergent
If L > 1 or 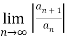 =
= then
then 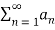 is divergent
is divergent
If L=1 then the series is inconclusive.
Q 11: L = 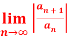
Solution: 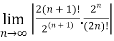
= 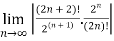
= 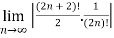
= 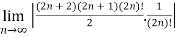
=
=
Q12: 

=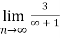
= 0
Therefore, the series converges since, 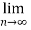 is 0.
is 0.
Nth root test:
If 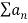 is a series with positive terms and
is a series with positive terms and  =L then,
=L then,
The series converges if L < 1
The series diverges if L>1
The test is in conclusive if L=1
Note: These rules are same for ratio test.
Q 13:
 n=
n= 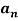
=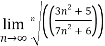 n =
n = 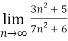 =
= <1
<1
Therefore, the series is convergent by root test.
Q 14: L= 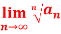
Solution: 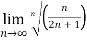 n
n
= 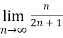
= ½
Therefore, the series is convergent
Leibnitz test:
Leibnitz test is an alternative way of expressing derivatives to ff’(x),g’(x),etc.,
If y is expressed in terms of x then the derivative is written as 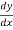
Q 15:
Y = 3x2 – 7x
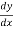 = 6x-7
= 6x-7
Q 16: Q = 9R2-  to find
to find 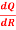
Solution:
Q = 9R2-15R-3
Now,
 = 18R+45R-2 = 18R +
= 18R+45R-2 = 18R +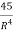
Power series:
A power series can be written in the form of

It can be written in the form of a function as.,
f(x) =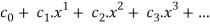
If we let  =1 for all n then the power series tends to geometric series
=1 for all n then the power series tends to geometric series
f(x) = 1+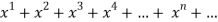
The above series converges, if -1<x<1
The above series diverges if x≥ 1 and x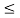 -1
-1
Q 17:
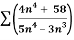 n
n
Solution: L=  =
= 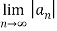 1/n
1/n
L= 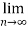
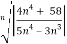 n =
n =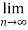
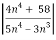
=  <1
<1
Hence the series converges.
Q 18:
Find the Taylor series for the following:
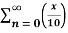
 =
= 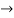
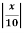 <1
<1
 (x/10)<1 and (x/10) > -1
(x/10)<1 and (x/10) > -1
Therefore, radius of convergence is (-10,10)
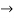 ROC =10
ROC =10
Q 19: f(n)5 = 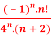
Solution: Here the ROC is 4
McLaurin series:
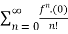 (x)n
(x)n
Q 20: f(x)=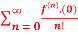
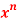
Solution: = f(0)+f’(0)x+ x2 +
x2 + 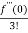 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
=