Question Bank
UNIT 5
Question Bank
UNIT 5
Question Bank
UNIT 5
Centroid and Centre of Gravity
Question 1) Difference between centre of gravity and centroid.
Answer:
Difference Between Center of Gravity and Centroid | |
Center of Gravity | Centroid |
The point where the total weight of the body focuses upon | It is referred to the geometrical center of a body |
It is the point where the gravitational force (weight) acts on the body | It is referred to the center of gravity of uniform density objects |
It is denoted by g | It is denoted by c |
Center of Gravity in a uniform gravitational field is the average of all points, weighted by local density or specific weight | The centroid is a point in a plane area in such a way that the moment of area about any axis throughout that point is 0 |
It is a physical behavior of the object, a point where all the weight of an object is acting | It is a geometrical behavior. It is the center of measure of the amount of geometry. |
Question 2) A long rod of length 20 meters has a mass of 100 kg. There is a 25 kg mass at the left end. Where is the center of gravity relative to the left end?
Answer:
We will use the center of gravity equation to determine the location of the center of mass. Weight is the mass times the acceleration due to gravity, 9.8 m/s2.
Weight 1 is the weight of the rod and weight 2 is the mass of the extra mass.
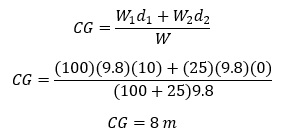 |
Notice that the accelerations due to gravity cancel. The center of mass of this system is 8 meters from the left end.
Question 3)Where would you place a 50 kg mass on a 75 kg, 14-meter rod so that its center of mass is 1 meter to the left of the physical center of the rod?
Answer:
We will not use the acceleration due to gravity in this solution.
Mass 1 is the mass of the rod and mass 2 is the extra mass.
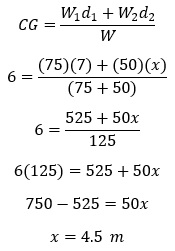 |
The 50 kg mass would have to be 4.5 meters from the left end.
Question 4) Explain centre of gravity.
Answer:
The centre of gravity of a body is the point through which the whole weight of the body acts. A body’s center of gravity is the point around which the resultant torque due to gravity forces vanishes. Where a gravity field can be considered to be uniform and the centre of gravity will be the same.
Question 5)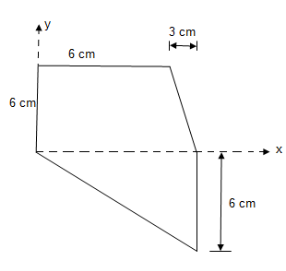
Locate the centroid of area of the following figure w.r.t. Given axis.
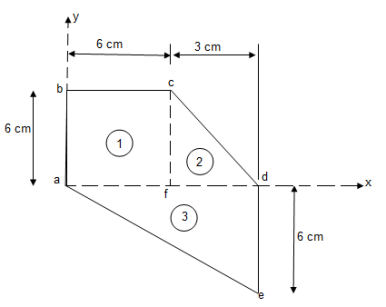
Solution:
Let us divide the given area as shown above into 3 simple parts.
Consider area ① i.e. Square abcd,
 of□avcd = A1 =
of□avcd = A1 =  = 36 cm2
= 36 cm2
X1 =  = 3 cm
= 3 cm
y1 =  = 3 cm
= 3 cm
Consider area ② i.e. lecfd,
lecfd,
 A2 = area of
A2 = area of  cfd =
cfd = 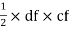

A2 = 9 cm2
X2 = 6 +  = 6 +
= 6 +  = 7 cm
= 7 cm
Y2 =  =
=  = 2 cm
= 2 cm
Consider area ③ i.e. ade,
ade,
 area of
area of 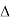 ade =
ade = 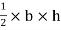
A3 = 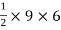
A3 = 27 cm2
X3 = 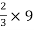 = 6 cm
= 6 cm
y3 = 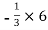 = -2 cm
= -2 cm
Now
X = 
= 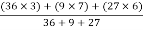
X = 4.625 cm
Y = 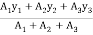
= 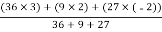
Y = 1 cm
 co-ordinate of centroid of the given area are
co-ordinate of centroid of the given area are
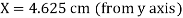
Y = 1 cm (from x axis)
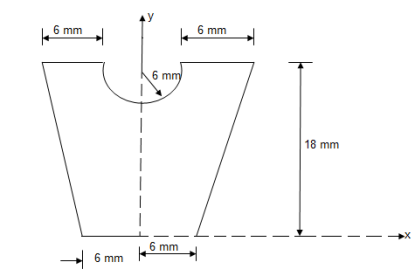
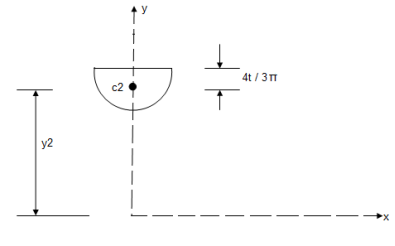
Question 6) Determine the Y co-ordinate of the centroid of the shaded area as shown in figure
Answer:
Consider trapezoid as area ① and semicircle as area ②
 For trapezoid and semicircle, shaded area is symmetrical about Y axis and thus as Y axis passing through symmetry line, X = 0
For trapezoid and semicircle, shaded area is symmetrical about Y axis and thus as Y axis passing through symmetry line, X = 0
1) 
For trapezoid :
A1 = 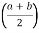 h
h
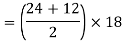
A1 = 324 mm2
Y1 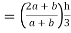
Y1  = 10 mm
= 10 mm
2) For semicircle :
A2 =  = =
= = 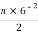 = 56.55 mm2
= 56.55 mm2
Y2 = 18 - 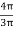 = 18 -
= 18 - 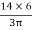 = 15.45 mm
= 15.45 mm
Y =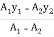 =
= 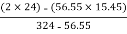 =
=
 y = 8.84 mm
y = 8.84 mm
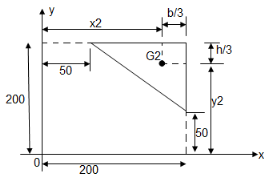
Question 7)Locate the centroid of shaded lamina as shown in figure?
Answer:
Let us split given composite
Area into simple parts
Area ① - square
Area ② - triangle
Area ③ - quarter circle
 1.
1.
A1 = 2002 = 40000 mm2
X1 = Y1 = 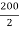 = 100 mm
= 100 mm
 2.
2.
 A2 =
A2 = 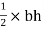
= 
= 11250 mm2
 X2 = 200 –
X2 = 200 – 
X2 = 200 – 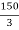 = 150 mm
= 150 mm
 y2 = 200 –
y2 = 200 –  = 200 –
= 200 – 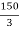 = 150 mm
= 150 mm
3.
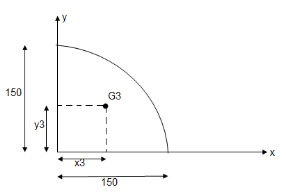
 A3 =
A3 = 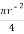 =
= 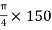 2
2
 A3= 17671.46 mm2
A3= 17671.46 mm2
 x3 = y3 =
x3 = y3 = 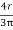 =
= 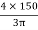
 x3 = y3 = 63.66 mm
x3 = y3 = 63.66 mm
X =  = 107.91 mm
= 107.91 mm
Y = 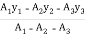 = 107.91 mm
= 107.91 mm
Question 8) Locate the centroid of shaded lamina as shown in fig.
Answer:
Consider the composite area
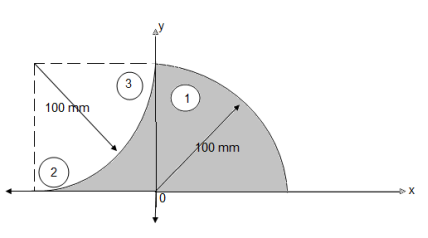
Shown in figure:
Let us split thus composite area into simple parts thus
Area ① - quarter circle (shaded)
Area ② - square
Area ③ - quarter circle (non-shaded)

- Area ①
A1 =  =
= 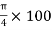 2 = 7854 mm2
2 = 7854 mm2
X1 = 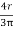 =
=  = 42.44 mm
= 42.44 mm
Y1 =  = 42.44 mm
= 42.44 mm
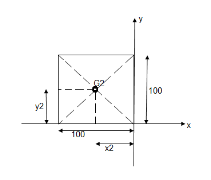 Area ②
Area ②
A2 = 100  100 = 10000 mm2
100 = 10000 mm2
X2 = 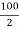 = -50 mm
= -50 mm
Y2 = 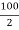 = 50 mm
= 50 mm
 Area ③
Area ③
A3 = 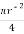 =
= 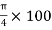 2 = 7854 mm2
2 = 7854 mm2
X3 =  = 57.56 mm
= 57.56 mm
Y3 = 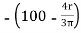 = 57.56 mm
= 57.56 mm
 Centroid of shaded portion will be
Centroid of shaded portion will be
X = 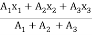
= 
= 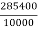
X = 28.54 mm
 Y =
Y = 
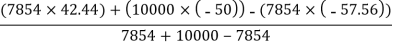
= 
Y= 38.12 mm
Centroid of shaded lamina will be at (28.54 mm, 38.12 mm)
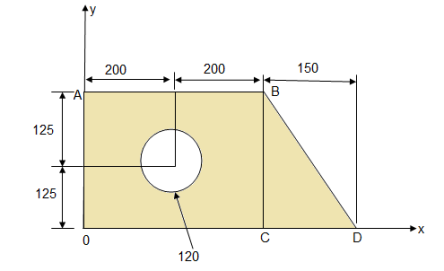
Question 9)Determine the X co-ordinate of the centroid of shaded area with respect to origin 0 as shown in figure.
Answer:
- Consider rectangle O A B C
 area = A1 = 400
area = A1 = 400  250 = 100000 mm2
250 = 100000 mm2
X1 = 200 mm
2. Consider right angle  B C D
B C D
 area = A2 =
area = A2 = 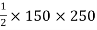
 mm2
mm2
X2 = 400 + 
= 400 + 
X2 = 450 mm
3. Consider circle of  120 mm
120 mm
Area = A3 = 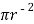
A3 = 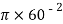 = 11309.73 mm2
= 11309.73 mm2
X3 = 200 mm
Thus  X =
X = 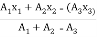
= 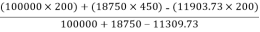
 X = 242.52 mm
X = 242.52 mm
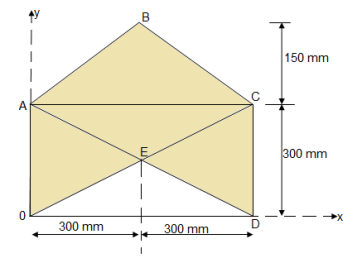
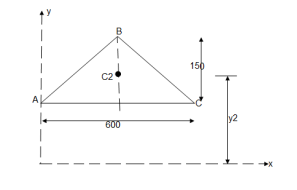
Question 10) Determine the co-ordinate of centroid of the shaded area as shown in figure
Answer:
The given figure and Shaded area is Symmetrical about y axis Shaded area,
X = 300 mm
Let us divide the given diagram into 3 parts
 ①rectangle O A C D , ②
①rectangle O A C D , ② A B C , ③
A B C , ③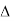 O E D
O E D
①for rectangle O A C D
A1 = 600 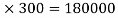 mm2
mm2
Y1 = 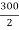 = 150 mm
= 150 mm
 ②for
②for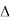 A B C
A B C
A2 = 
= 
= 45000 mm2
Y2 = 300 + 
Y2 = 300 + (150/3) = 350 mm
 ③For O E D
③For O E D
A3 = 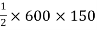 = 45000 mm2
= 45000 mm2
Y3 =  = 150/3 = 50 mm
= 150/3 = 50 mm
Y = 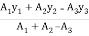
= 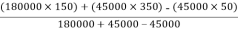
Y = 225 mm