Unit 2 question
- Find the median score of 7 students in science class
Solution
Score = 19, 17, 16, 15, 12, 11, 10
Median = (7+1)/2 = 4th value
Median = 15
2. find the median of the table given below
Marks obtained | No. Of students |
20 | 6 |
25 | 20 |
28 | 24 |
29 | 28 |
33 | 15 |
38 | 4 |
42 | 2 |
43 | 1 |
Solution
Marks obtained | No. Of students | Cf |
20 | 6 | 6 |
25 | 20 | 26 (20+6) |
28 | 24 | 50 (26+24) |
29 | 28 | 78 |
33 | 15 | 93 |
38 | 4 | 97 |
42 | 2 | 99 |
43 | 1 | 100 |
Median = (n+1)/2 = 100+1/2 = 50.5
Median = (28+29)/2 = 28.5
3. Calculate the median
Marks | No. Of students |
0-4 | 2 |
5-9 | 8 |
10-14 | 14 |
15-19 | 17 |
20-24 | 9 |
Solution
Marks | No. Of students | CF |
0-4 | 2 | 2 |
5-9 | 8 | 10 |
10-14 | 14 | 24 |
15-19 | 17 | 41 |
20-24 | 9 | 50 |
| 50 |
|
n = 50
n = 50/2= 25
2
The category containing n/2 is 15 -19
Lb = 15
Cfp = 24
f = 17
Ci = 4
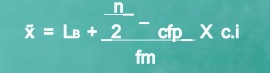
Median = 15 + 25-24 *4 = 15.23
17
4. In a class of 30 students marks obtained by students in science out of 50 is tabulated below. Calculate the mode of the given data.
Marks obtained | No. Of students |
10 -20 | 5 |
20 – 30 | 12 |
30 – 40 | 8 |
40 - 50 | 5 |
Solution
The group with the highest frequency is the modal group: - 20 -30
D1 = 12 - 5 = 7
D2 = 12 - 8 = 4
Mode = L1 + (L2 – L1) d1
d1 +d2
mode = 20 + (30-20) 7 = 20+10 (7/11) = 26.36
7+4
Mode = 61.8
5. The following data represent the income distribution of 100 families. Calculate mean income of 100 families?
Income |
| 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
No. Of families |
| 8 | 12 | 25 | 22 | 16 | 11 | 6 |
Solution
Income | No. Of families | Xm (Mid point) | FXm |
30-40 | 8 | 35 | 280 |
40-50 | 12 | 34 | 408 |
50-60 | 25 | 55 | 1375 |
60-70 | 22 | 65 | 1430 |
70-80 | 16 | 75 | 1200 |
80-90 | 11 | 85 | 935 |
90-100 | 6 | 95 | 570 |
| n = 100 |
| ∑f Xm = 6198 |
X = ∑f Xm/n = 6330/100 = 63.30
Mean = 63.30
6. calculate the geometric mean
X | f |
60 – 80 | 22 |
80 – 100 | 38 |
100 – 120 | 45 |
120 – 140 | 35 |
|
|
Solution
X | f | Mid X | Log X | f log X |
60 – 80 | 22 | 70 | 1.845 | 40.59 |
80 – 100 | 38 | 90 | 1.954 | 74.25 |
100 – 120 | 45 | 110 | 2.041 | 91.85 |
120 – 140 | 35 | 130 | 2.114 | 73.99 |
Total | 140 |
|
| 280.68 |
GM = Antilog ∑ f logxi
N
= antilog 280.68/140
= antilog 2.00
GM = 100
7. calculate harmonic mean
Class | Frequency |
2-4 | 3 |
4-6 | 4 |
6-8 | 2 |
8-10 | 1 |
Solution
Class | Frequency | x | f/x |
2-4 | 3 | 3 | 1 |
4-6 | 4 | 5 | 0.8 |
6-8 | 2 | 7 | 0.28 |
8-10 | 1 | 9 | 0.11 |
| 10 |
| 2.19 |
Harmonic mean = 10/2.19 = 4.55
8. Compute 5-year, 7-year and 9-year moving averages for the following data.
Year | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
Values | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 |
Solution
|
| 5-Year Moving | 7-Year Moving | 9-Year Moving | |||
Years | Values | Total | Average | Total | Average | Total | Average |
1990 | 2 |
|
|
|
|
|
|
1991 | 4 |
|
|
|
|
|
|
1992 | 6 | 30 | 6 |
|
|
|
|
1993 | 8 | 40 | 8 | 56 | 8 |
|
|
1994 | 10 | 50 | 10 | 70 | 10 | 90 | 10 |
1995 | 12 | 60 | 12 | 84 | 12 | 108 | 12 |
1996 | 14 | 70 | 14 | 98 | 14 | 126 | 14 |
1997 | 16 | 80 | 16 | 112 | 16 |
|
|
1998 | 18 | 90 | 18 |
|
|
|
|
1999 | 20 |
|
|
|
|
|
|
2000 | 22 |
|
|
|
|
|
|
9. Compute 4-year moving averages centered for the following time series:
Year | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 |
|
Values | 80 | 90 | 92 | 83 | 87 | 96 | 100 | |
Solution
|
| 4-Year Moving |
| ||
Years | Values | Total | Average | 2 valus moving total | 4 year moving average centered |
1990 | 80 |
|
|
|
|
1991 | 90 | 345 | 86.25 |
|
|
1992 | 92 | 352 | 88 | 174.25 | 87.125 |
1993 | 83 | 358 | 89.5 | 177.5 | 88.75 |
1994 | 87 | 366 | 91.5 | 181 | 90.5 |
1995 | 96 | 393 | 98.25 | 189.75 | 94.875 |
1996 | 100 |
|
|
|
|
1997 | 110 |
|
|
|
|
10. For a moderately skewed distribution , the median is 20 and the mean is 22.5. Using these values, find the approximate value of the mode.
Solution:
Given,
Mean = 22.5
Median = 20
Mode = x
Now, using the relationship between mean mode and median we get,
(Mean – Mode) = 3 (Mean – Median)
So,
∴ x = 15
So, Mode = 15.
