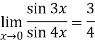UNIT 2
UNIT 2
UNIT 2
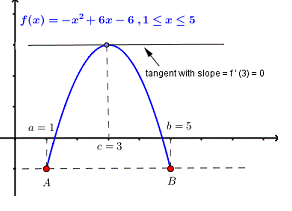
Q:1 Solve the given graph by Rolle’s theorem


Solution: Given 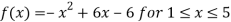 and
and
f(1) =f(5) =-1
Since by Rolle’s theorem, there exists at least one value of x=0 such that 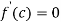
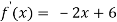
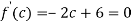
Solve the above equation to obtain
C=3
Therefore at x=3 there is a tangent to the graph of f that has a slope equal to zero (horizontal line ) as shown in figure below.
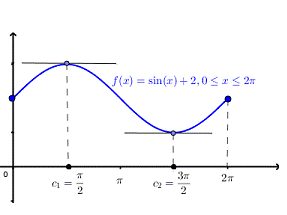
Q:2 Solve the given graph by Rolle’s theorem  is shown below .f(0)=f(
is shown below .f(0)=f(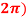 =2 and f is continous on
=2 and f is continous on  and differentiable on (0,
and differentiable on (0,
Solution: Given 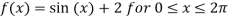 and f(0)=f(
and f(0)=f(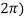 =2
=2
Since by Rolle’s theorem, there exists at least one value of x=c such that 
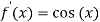
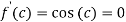
The above equation has two solutions on the interval 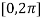
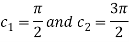
Therefore both at x= and x=3
and x=3  there are tangents to the graph that have a slope equal to zero (horizontal line ) as shown in figure below.
there are tangents to the graph that have a slope equal to zero (horizontal line ) as shown in figure below.
Q: 3: Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in 
Solution: Here f(x) = ex(sin x – cos x); 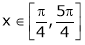
i) Ex is an exponential function continuous for every 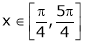 also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in
also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 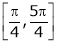 and Hence ex(sin x – cos x) is continuous in
and Hence ex(sin x – cos x) is continuous in 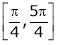 .
.
Ii) Consider
f(x) = ex(sin x – cos x)
Diff. w.r.t. x we get
f’(x) = ex(cos x + sin x) + ex(sin x + cos x)
= ex[2sin x]
Clearly f’(x) is exist for each 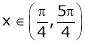 & f’(x) is not infinite.
& f’(x) is not infinite.
Hence f(x) is differentiable in 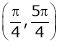 .
.
Iii) Consider
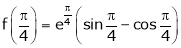
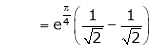
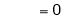
Also,
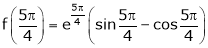
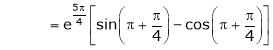
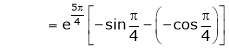
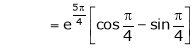
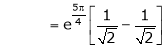

Thus 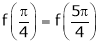
Hence all the conditions of Rolle’s theorem are satisfied, so there exist 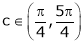 such, that
such, that
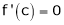
i.e. 
i.e. sin c = 0

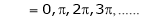
But
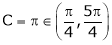
Hence Rolle’s theorem is verified.
Q:4 Use LaGrange’s mean value theorem to determine a point P on the curve y=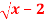
Where the tangent is parallel to the chord joining (2,0) and (3,1)
Solution: Consider y= 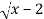 in [2,3]
in [2,3]
(i) Function is continuous in[2,3] as algebraic expression with positive exponent is continuous.
(ii) y’= 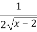 , y’ exists in (2,3) hence the function is derivable in (2,3)
, y’ exists in (2,3) hence the function is derivable in (2,3)
Hence the condition of LMV theorem is satisfied.
Hence, there exists one c in (2,3) such that 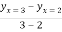 =
= 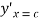
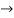
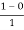 =
= 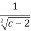
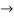 4(c-2) = 1
4(c-2) = 1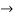 4c=9
4c=9 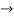 c= 4/9
c= 4/9
 for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)
for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)
Substituting in (i) we get,
Y= 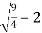 =
= 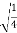 = ½
= ½
Q: 5: Verify lagrange’s mean value theorem for the following function
f(x) = 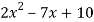
Putting x=a=2 and x=b=5 ,we get
f(2) = 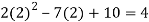
f(5) = 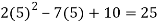
Clearly,
f(2) 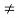 f(5)
f(5)
Since f(x) is a polynomial function in x, then f(x) is continuous in [2,5].
And f(x) is polynomial in x ,then it can be differentiate such that f’(x) = 4x-7
Then by LMV theorem there exists c 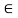 (2,5) such that’
(2,5) such that’
f’ (c) = 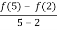
4c-7 = 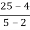
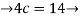 c=3.75
c=3.75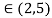
Hence lagrange’s mean value theorem is verified for f(x) in [2,5].
Q:6: Verify the Lagrange’s mean value theorem for
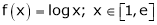
Solution: Here f(x) = logx and x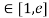
i) Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]
Ii) Consider f(x) = log x.
Diff. w.r.to, x we get,
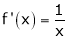
Clearly f’(x) exists for each value of x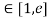 & is finite.
& is finite.
Hence all conditions of LMVT are satisfied Hence at least c 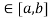
Such that
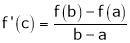
i.e. 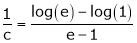
i.e. 
i.e. 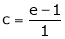
i.e. 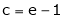
Since e = 2.7183
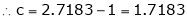
Clearly c = 1.7183 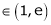
Hence LMVT is verified.
Q: 7: Verify mean value theorem for f(x) = tan-1x in [0, 1]
Solution: Here 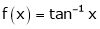 ;
; 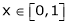
i) Clearly 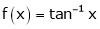 is an inverse trigonometric function and hence it is continuous in [0, 1]
is an inverse trigonometric function and hence it is continuous in [0, 1]
Ii) Consider 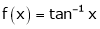
Diff. w.r.t. x we get,
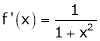
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite
Hence all conditions of LMVT are satisfied, Thus there exist 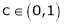
Such that
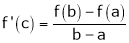
i.e. 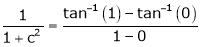
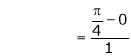
i.e. 
i.e. 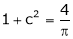
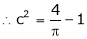
i.e. 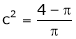
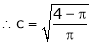
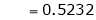
Clearly 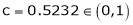
Hence LMVT is verified.
Q:8: Verify Cauchy mean value theorems for 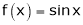 &
&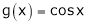 in
in 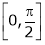 Solution :Let
Solution :Let 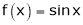 &
& ;
; 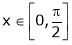
i) Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in 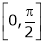
Ii) Since 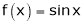 &
&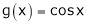
Diff. w.r.t. x we get,
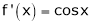 &
&
Clearly both f’(x) and g’(x) exist & finite in 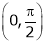 . Hence f(x) and g(x) is derivable in
. Hence f(x) and g(x) is derivable in 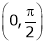 and
and
Iii) 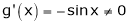
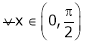
Hence by Cauchy mean value theorem, there exist at least 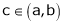 such that
such that
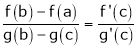
i.e. 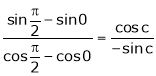
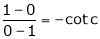
i.e. 1 = cot c

i.e. 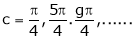
Clearly 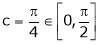
Hence Cauchy mean value theorem is verified.
Q:9 : Considering the functions ex an e-x, show that c is arithmetic mean of a & b.
Solution: Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b].
i) Consider 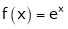 &
&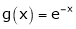
Diff. w.r.t. x we get
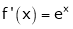 and
and 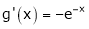
Clearly f(x) and g(x) are derivable in (a, b)
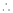 By Cauchy’s mean value theorem
By Cauchy’s mean value theorem 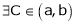 such that
such that
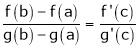
i.e. 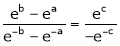
i.e. 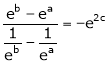
i.e. 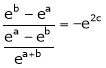
i.e. 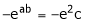
i.e. 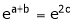
i.e. 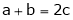
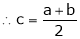
Thus 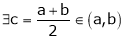
i.e. c is arithmetic mean of a & b.
Hence the result
Q:10:
Find the Taylor series for the following:

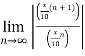 =
= 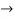
 <1
<1
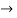 (X/10)<1 and (x/10) > -1
(X/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
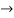 ROC =10
ROC =10
Example 2:
f(n)5 = 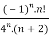
Here the ROC is 4
Q:11Compute the Taylor series centered at zero for f(x)= sinx
Solution:
f(x)=sinx f(0)=0
f’(x) =cosx f’(0)=1
f’’(x)=-sinx f’’(0)=0
f’’’(x) = -cosx f’’’(0)=-1
f(4)(x)= cosx f(4) (0)= 1
Applying Taylor series we get
T(x) = 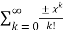 =
= 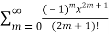 = x-
= x-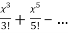
Thus turns out to converge x to sinx.
Maclaurian series:
Q:12 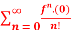 (x)n
(x)n
Solution:
f(x)=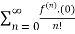
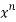
= f(0)+f’(0)x+ x2 +
x2 + 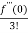 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 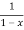
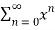
Q:13: Find the Maclaurian series for f(x)= ex
Solution:
To get Maclaurian series, we look at the Taylor series polynomials for f near 0 and let them keep going.
Considering for example 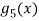
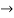
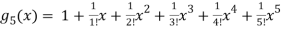
By Maclaurian series we get,
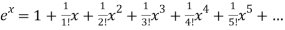 +
+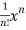
Q:14
Find out the maxima and minima of the function
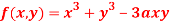
Solution:
Given 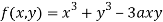 …(i)
…(i)
Partially differentiating (i) with respect to x we get
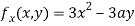 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
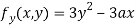 ….(iii)
….(iii)
Now, form the equations 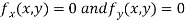
Using (ii) and (iii) we get
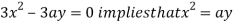
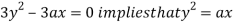
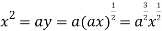 using above two equations
using above two equations
Squaring both side we get
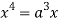
Or 
This show that 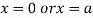
Also we get 
Thus we get the pair of value as 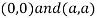
Now, we calculate
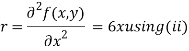
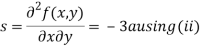
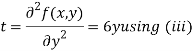
Putting above values in
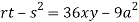
At point (0,0) we get
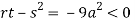
So, the point (0,0) is a saddle point.
At point 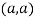 we get
we get
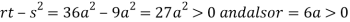
So the point 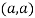 is the minimum point where
is the minimum point where 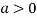
In case 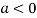
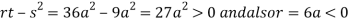
So the point 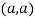 is the maximum point where
is the maximum point where 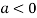
Q:15
Find the maximum and minimum point of the function
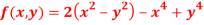
Partially differentiating given equation with respect to and x and y then equate them to zero
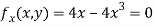
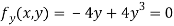
On solving above we get 
Also 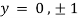
Thus we get the pair of values (0,0), (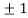 ,0) and (0,
,0) and (0,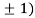
Now, we calculate
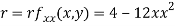
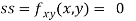
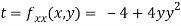
At the point (0,0)
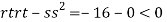
So function has saddle point at (0,0).
At the point (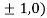

So the function has maxima at this point (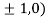 .
.
At the point (0,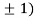
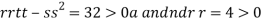
So the function has minima at this point (0,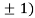 .
.
At the point (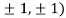
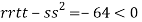
So the function has an saddle point at (
Q:16 Find the maximum and minimum value of 
Let 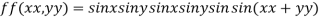
Partially differentiating given function with respect to x and y and equate it to zero
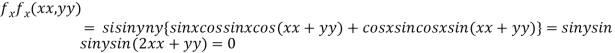 ..(i)
..(i)
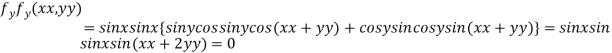 ..(ii)
..(ii)
On solving (i) and (ii) we get
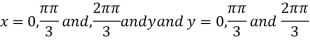
Thus pair of values are 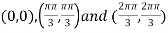
Now, we calculate
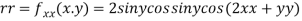
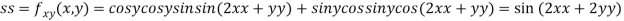
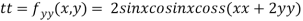
At the point (0,0)
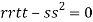
So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x, 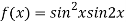
At the point 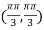
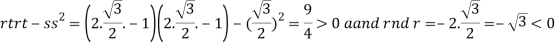
So that the given function has maximum value at 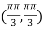
Therefore maximum value of given function
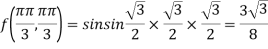
At the point 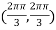
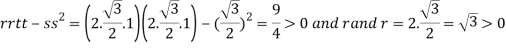
So that the given function has minimum value at 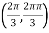
Therefore minimum value of the given function
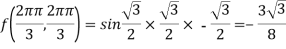
Q:17: Evaluate
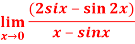
Solution:
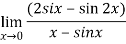
Differentiate the above form ,we get
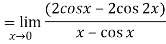
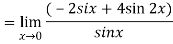

Now substitute the limit,
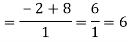
Therefore ,
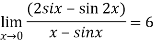
Q:18: Evaluate
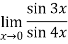
Given,
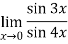
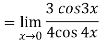
Now substitute the limit
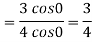
Therefore ,
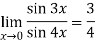
UNIT 2
UNIT 2
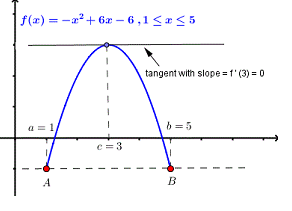
Q:1 Solve the given graph by Rolle’s theorem


Solution: Given 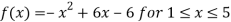 and
and
f(1) =f(5) =-1
Since by Rolle’s theorem, there exists at least one value of x=0 such that 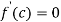
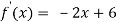
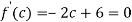
Solve the above equation to obtain
C=3
Therefore at x=3 there is a tangent to the graph of f that has a slope equal to zero (horizontal line ) as shown in figure below.
Q:2 Solve the given graph by Rolle’s theorem  is shown below .f(0)=f(
is shown below .f(0)=f(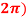 =2 and f is continous on
=2 and f is continous on  and differentiable on (0,
and differentiable on (0,
Solution: Given 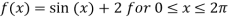 and f(0)=f(
and f(0)=f(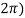 =2
=2
Since by Rolle’s theorem, there exists at least one value of x=c such that 
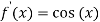
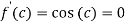
The above equation has two solutions on the interval 
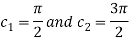
Therefore both at x= and x=3
and x=3  there are tangents to the graph that have a slope equal to zero (horizontal line ) as shown in figure below.
there are tangents to the graph that have a slope equal to zero (horizontal line ) as shown in figure below.
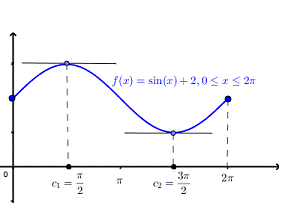
Q: 3: Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in 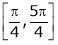
Solution: Here f(x) = ex(sin x – cos x); 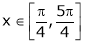
i) Ex is an exponential function continuous for every 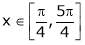 also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in
also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 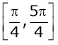 and Hence ex(sin x – cos x) is continuous in
and Hence ex(sin x – cos x) is continuous in 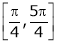 .
.
Ii) Consider
f(x) = ex(sin x – cos x)
Diff. w.r.t. x we get
f’(x) = ex(cos x + sin x) + ex(sin x + cos x)
= ex[2sin x]
Clearly f’(x) is exist for each 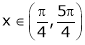 & f’(x) is not infinite.
& f’(x) is not infinite.
Hence f(x) is differentiable in 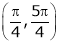 .
.
Iii) Consider
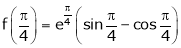
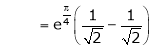
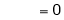
Also,
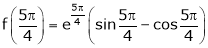
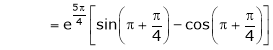
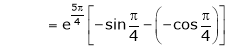
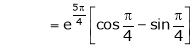
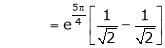

Thus 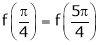
Hence all the conditions of Rolle’s theorem are satisfied, so there exist 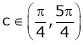 such, that
such, that
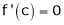
i.e. 
i.e. sin c = 0

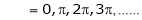
But
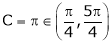
Hence Rolle’s theorem is verified.
Q:4 Use LaGrange’s mean value theorem to determine a point P on the curve y=
Where the tangent is parallel to the chord joining (2,0) and (3,1)
Solution: Consider y= 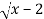 in [2,3]
in [2,3]
(i) Function is continuous in[2,3] as algebraic expression with positive exponent is continuous.
(ii) y’= 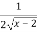 , y’ exists in (2,3) hence the function is derivable in (2,3)
, y’ exists in (2,3) hence the function is derivable in (2,3)
Hence the condition of LMV theorem is satisfied.
Hence, there exists one c in (2,3) such that 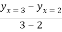 =
= 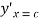
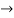
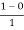 =
= 
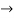 4(c-2) = 1
4(c-2) = 1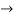 4c=9
4c=9 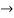 c= 4/9
c= 4/9
 for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)
for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)
Substituting in (i) we get,
Y= 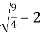 =
= 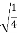 = ½
= ½
Q: 5: Verify lagrange’s mean value theorem for the following function
f(x) = 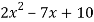
Putting x=a=2 and x=b=5 ,we get
f(2) = 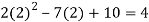
f(5) = 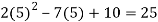
Clearly,
f(2) 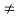 f(5)
f(5)
Since f(x) is a polynomial function in x, then f(x) is continuous in [2,5].
And f(x) is polynomial in x ,then it can be differentiate such that f’(x) = 4x-7
Then by LMV theorem there exists c 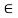 (2,5) such that’
(2,5) such that’
f’ (c) = 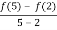
4c-7 = 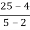
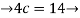 c=3.75
c=3.75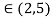
Hence lagrange’s mean value theorem is verified for f(x) in [2,5].
Q:6: Verify the Lagrange’s mean value theorem for
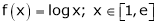
Solution: Here f(x) = logx and x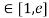
i) Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]
Ii) Consider f(x) = log x.
Diff. w.r.to, x we get,
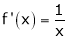
Clearly f’(x) exists for each value of x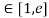 & is finite.
& is finite.
Hence all conditions of LMVT are satisfied Hence at least c 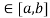
Such that
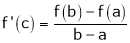
i.e. 
i.e. 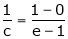
i.e. 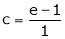
i.e. 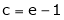
Since e = 2.7183
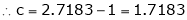
Clearly c = 1.7183 
Hence LMVT is verified.
Q: 7: Verify mean value theorem for f(x) = tan-1x in [0, 1]
Solution: Here 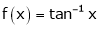 ;
; 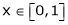
i) Clearly 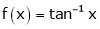 is an inverse trigonometric function and hence it is continuous in [0, 1]
is an inverse trigonometric function and hence it is continuous in [0, 1]
Ii) Consider 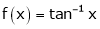
Diff. w.r.t. x we get,
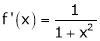
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite
Hence all conditions of LMVT are satisfied, Thus there exist 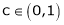
Such that
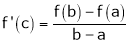
i.e. 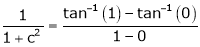
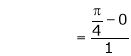
i.e. 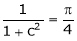
i.e. 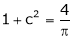
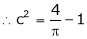
i.e. 
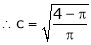
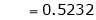
Clearly 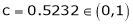
Hence LMVT is verified.
Q:8: Verify Cauchy mean value theorems for 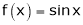 &
&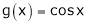 in
in 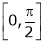 Solution :Let
Solution :Let 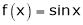 &
& ;
; 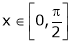
i) Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in 
Ii) Since 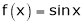 &
&
Diff. w.r.t. x we get,
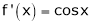 &
&
Clearly both f’(x) and g’(x) exist & finite in 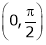 . Hence f(x) and g(x) is derivable in
. Hence f(x) and g(x) is derivable in 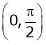 and
and
Iii) 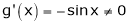
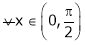
Hence by Cauchy mean value theorem, there exist at least 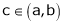 such that
such that
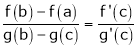
i.e. 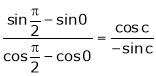
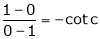
i.e. 1 = cot c

i.e. 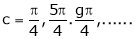
Clearly 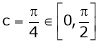
Hence Cauchy mean value theorem is verified.
Q:9 : Considering the functions ex an e-x, show that c is arithmetic mean of a & b.
Solution: Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b].
i) Consider  &
&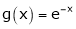
Diff. w.r.t. x we get
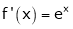 and
and 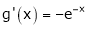
Clearly f(x) and g(x) are derivable in (a, b)
 By Cauchy’s mean value theorem
By Cauchy’s mean value theorem 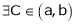 such that
such that
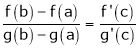
i.e. 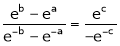
i.e. 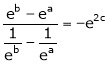
i.e. 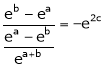
i.e. 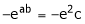
i.e. 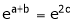
i.e. 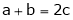
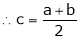
Thus 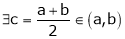
i.e. c is arithmetic mean of a & b.
Hence the result
Q:10:
Find the Taylor series for the following:
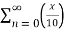
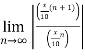 =
= 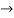
 <1
<1
 (X/10)<1 and (x/10) > -1
(X/10)<1 and (x/10) > -1
Therefore radius of convergence is (-10,10)
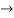 ROC =10
ROC =10
Example 2:
f(n)5 = 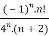
Here the ROC is 4
Q:11Compute the Taylor series centered at zero for f(x)= sinx
Solution:
f(x)=sinx f(0)=0
f’(x) =cosx f’(0)=1
f’’(x)=-sinx f’’(0)=0
f’’’(x) = -cosx f’’’(0)=-1
f(4)(x)= cosx f(4) (0)= 1
Applying Taylor series we get
T(x) = 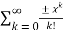 =
= 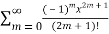 = x-
= x-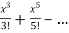
Thus turns out to converge x to sinx.
Maclaurian series:
Q:12 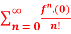 (x)n
(x)n
Solution:
f(x)=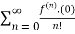

= f(0)+f’(0)x+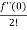 x2 +
x2 + 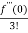 x3 +......
x3 +......
= 1+x+x2 +x3 + .....
= 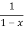

Q:13: Find the Maclaurian series for f(x)= ex
Solution:
To get Maclaurian series, we look at the Taylor series polynomials for f near 0 and let them keep going.
Considering for example 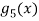
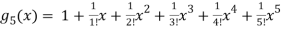
By Maclaurian series we get,
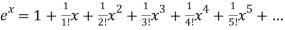 +
+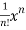
Q:14
Find out the maxima and minima of the function
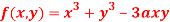
Solution:
Given  …(i)
…(i)
Partially differentiating (i) with respect to x we get
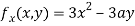 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
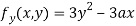 ….(iii)
….(iii)
Now, form the equations 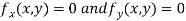
Using (ii) and (iii) we get
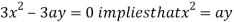
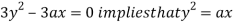
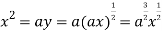 using above two equations
using above two equations
Squaring both side we get
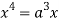
Or 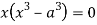
This show that 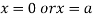
Also we get 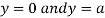
Thus we get the pair of value as 
Now, we calculate
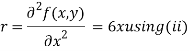
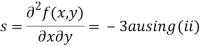
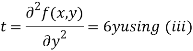
Putting above values in
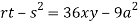
At point (0,0) we get
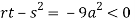
So, the point (0,0) is a saddle point.
At point  we get
we get
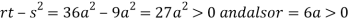
So the point  is the minimum point where
is the minimum point where 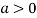
In case 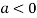
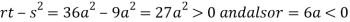
So the point 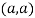 is the maximum point where
is the maximum point where 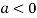
Q:15
Find the maximum and minimum point of the function
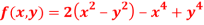
Partially differentiating given equation with respect to and x and y then equate them to zero
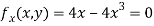
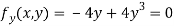
On solving above we get 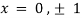
Also 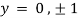
Thus we get the pair of values (0,0), (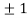 ,0) and (0,
,0) and (0,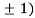
Now, we calculate
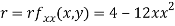
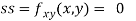
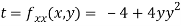
At the point (0,0)
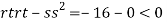
So function has saddle point at (0,0).
At the point (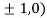
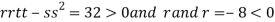
So the function has maxima at this point (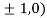 .
.
At the point (0,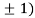
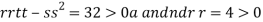
So the function has minima at this point (0,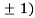 .
.
At the point (
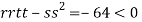
So the function has an saddle point at (
Q:16 Find the maximum and minimum value of 
Let 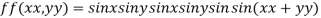
Partially differentiating given function with respect to x and y and equate it to zero
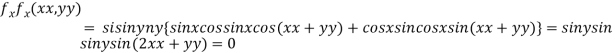 ..(i)
..(i)
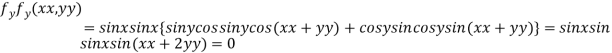 ..(ii)
..(ii)
On solving (i) and (ii) we get
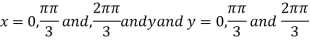
Thus pair of values are 
Now, we calculate
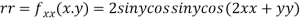
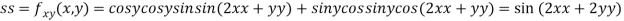
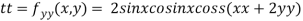
At the point (0,0)
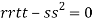
So further investigation is required
On the x axis y = 0 , f(x,0)=0
On the line y=x, 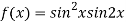
At the point 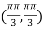
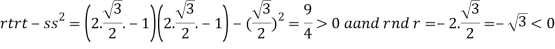
So that the given function has maximum value at 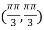
Therefore maximum value of given function
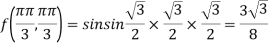
At the point 
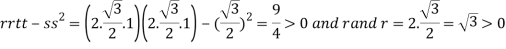
So that the given function has minimum value at 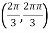
Therefore minimum value of the given function
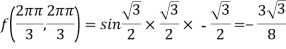
Q:17: Evaluate
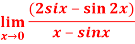
Solution:
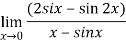
Differentiate the above form ,we get
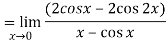
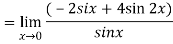
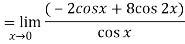
Now substitute the limit,
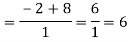
Therefore ,
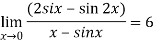
Q:18: Evaluate
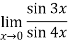
Given,
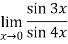
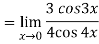
Now substitute the limit
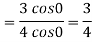
Therefore ,