Question Bank
Unit 01
Question Bank
Unit 01
Question Bank
Unit 01
Question Bank
Unit 01
Q-Explain the rules of LCAO.
Rules for the Linear Combination of Atomic Orbital are:-
- The combining atoms should have the same symmetry along the molecular axis for proper combination. e.g. All the sub-orbitals of 2p have same energy but still, the 2pz orbital of an atom can only combine with a 2pz orbital of another atom but cannot combine with 2px and 2py orbital as they have a different axis of symmetry.
- The two atomic orbital will combine to form molecular orbital. Greater is the extend of overlap of atomic orbital; greater will be the nuclear density.
- The combining atomic orbital must be of equal energy or approximately same energy.
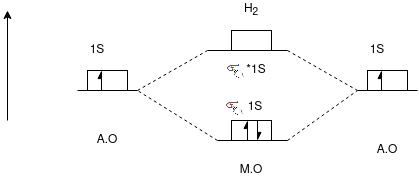
Q-Draw the energy level diagram of H2.
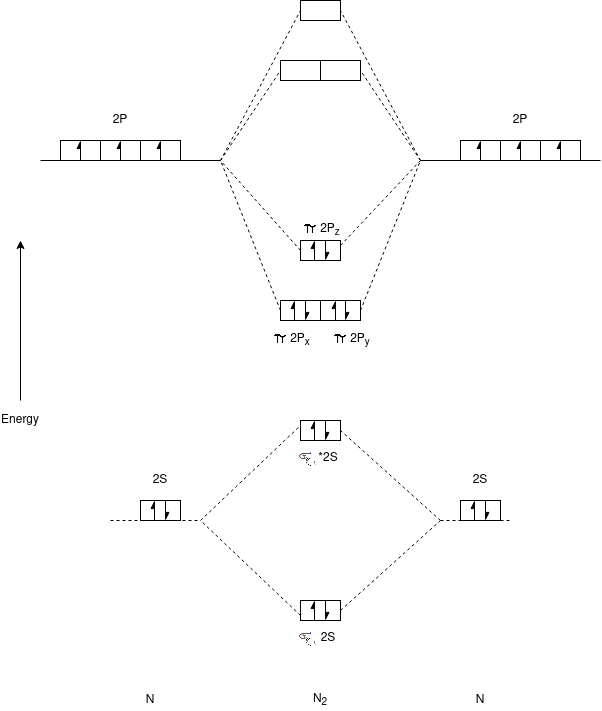
Q-Write electronic configuration and draw the energy level diagram of N2 molecule.
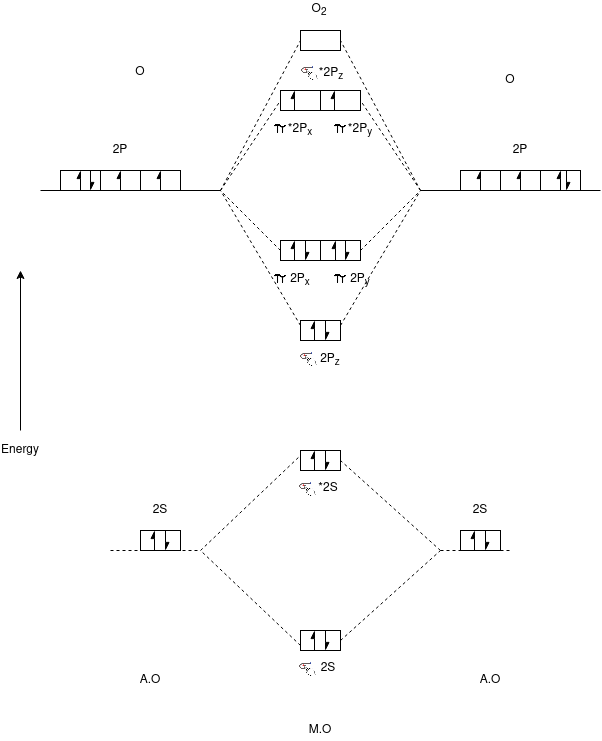
Q-Draw the energy level diagram of O2 molecule,.
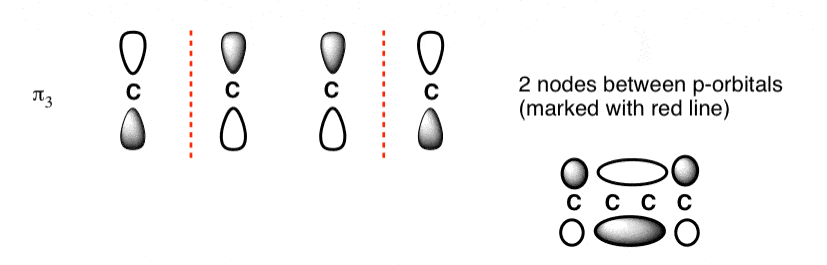
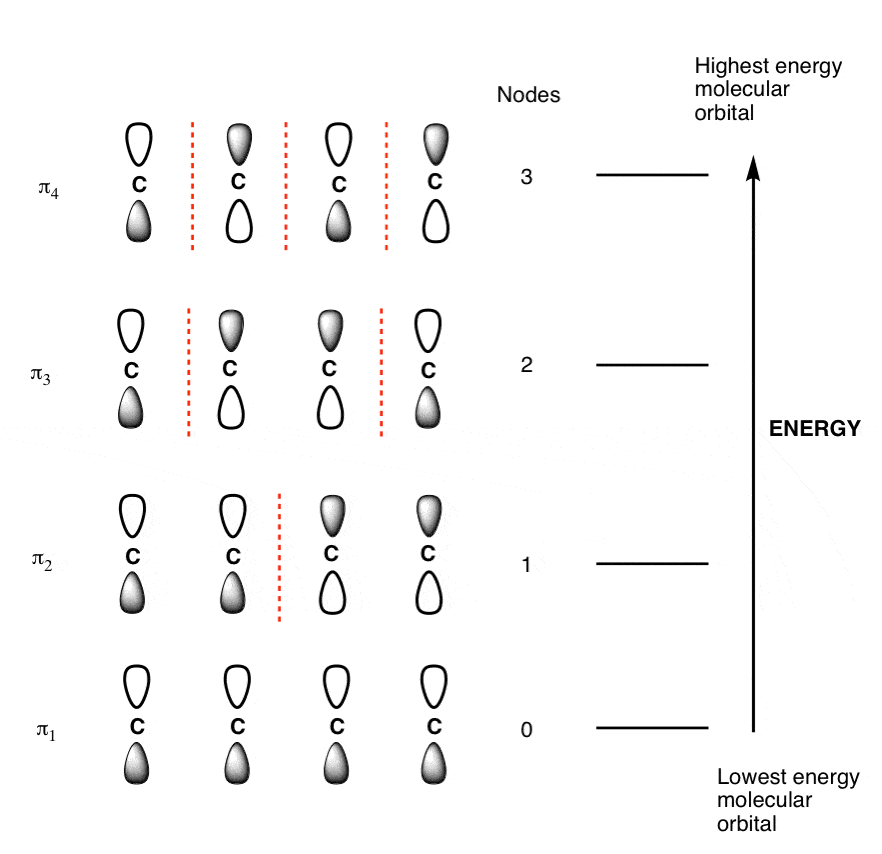
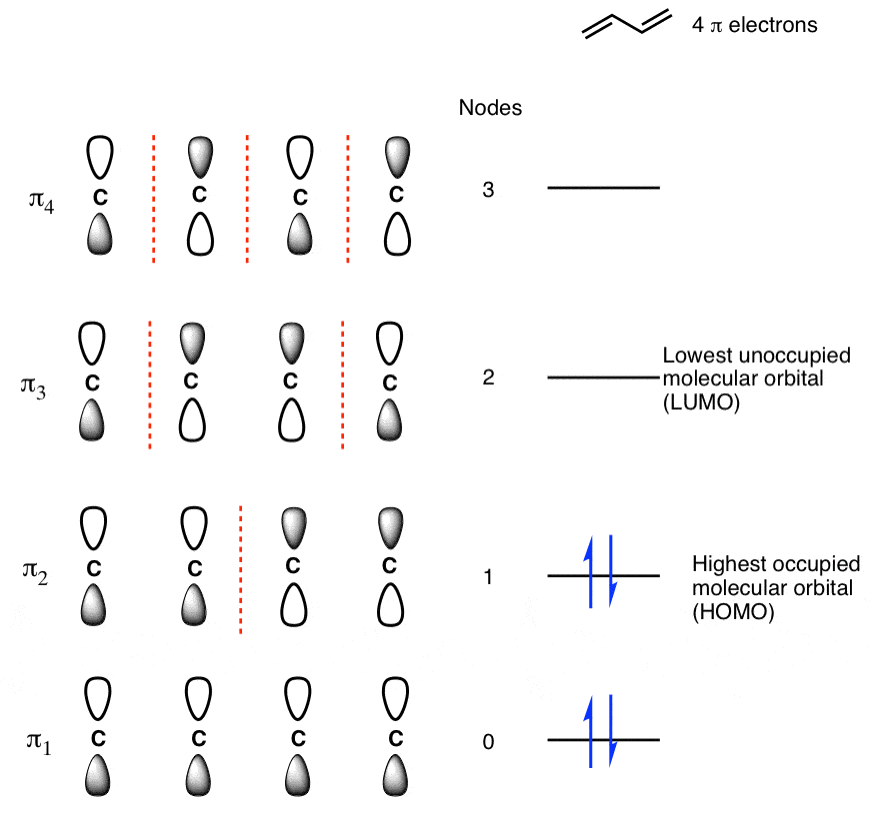
Q-Explain butadiene molecule.
The Butadiene Pi System has zero nodes at its lowest energy molecular orbital.
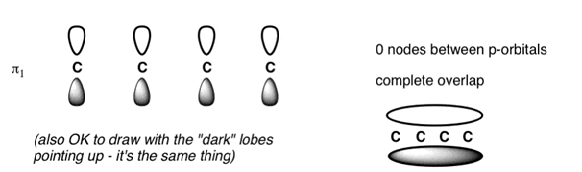
The Butadiene Pi System has three nodes at its lowest energy molecular orbital. The drawn n-p orbital are at alternate phase to each other. This create the a pi system with three nodes.

The Butadiene second lowest energy molecular orbital has one node.

The third lowest energy molecular orbital has two nodes.
The Full Molecular Orbital Diagram For The Butadienyl System.
Populating The Molecular Orbitals Of Butadiene With Electrons
Q-Explain Pi molecular orbital of benzene.
The Pi molecular orbital diagram for Benzene
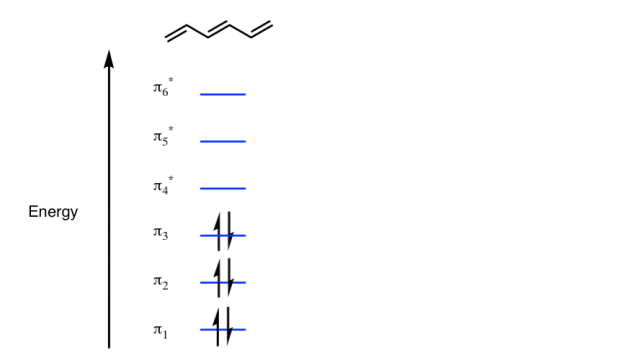
In the above increasing energy level the bottom three orbital are all bonding orbital while the top 3 orbital are anti bonding orbital.
The Benzene System has zero nodes at its lowest energy molecular orbital.
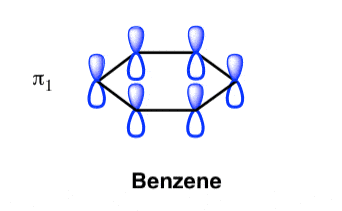
- All p orbital are aligned with phases pointing in the same direction.
- Nodes are absent between orbital.
- In this orbital, electrons are delocalized over the length of molecule, resulting in greatest lowering of energy.
Benzene Has Nodal Planes. The Maximum Energy Level Has 3 Nodal Planes
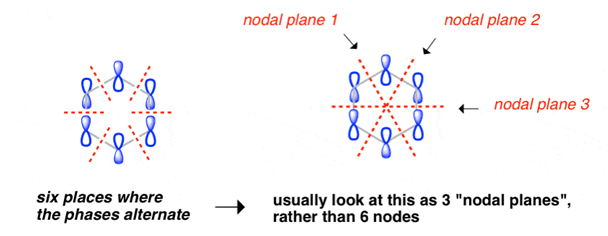
This orbital has zero overlap between adjacent p orbitals and therefore electrons in this orbital have the minimum possible delocalization. They are therefore the highest energy.
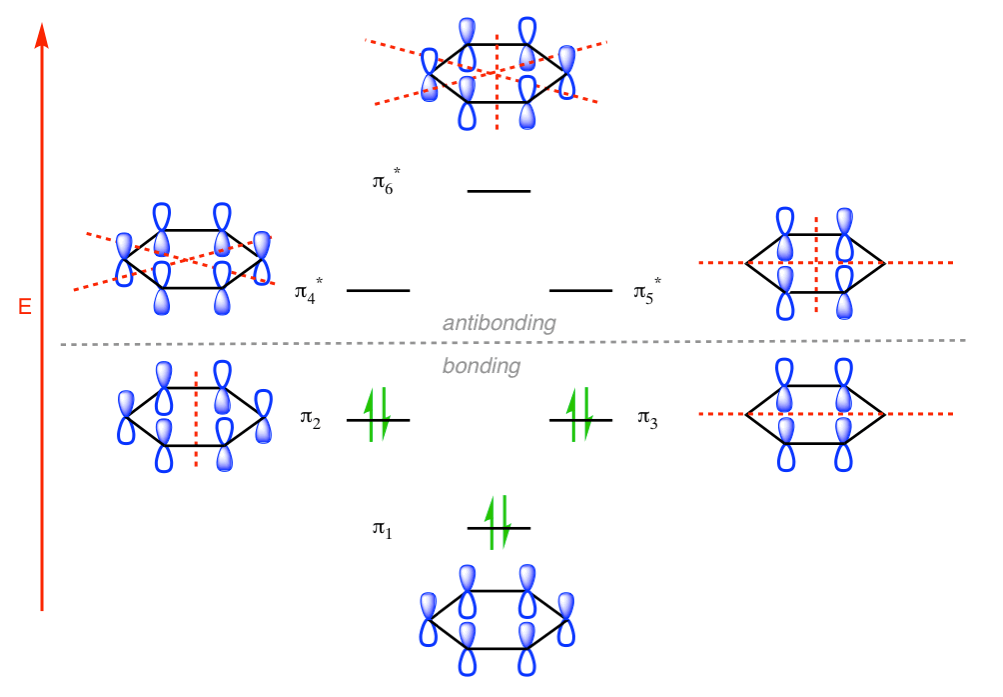
The pi molecular orbital of benzene
Q- What are the factors that affects the crystal field splitting d-orbitals.
The splitting can be affected by following factors:-
• Metal ion nature
• Metals oxidation state.
• Ligand arrangement around the metal ion
• Metal coordination number
Q-Explain spectrochemical series.
The ability of ligands to cause a large splitting of the energy between the orbital is essentially independent of the metal ion and the spectrochemical series is a list of ligands ranked in order of their ability to cause large orbital separations.
I< Br- < SCN- ~Cl- < F- < OH- ~ ONO- < C2O42- < H2O< NCS- < EDTA4-<NH3 ~ pyr ~ en < bipy < phen < CN- ~ CO
Q-Explain the crystal field theory of square planar complexes.
The crystal field stabilization energy (CFSE) is the stability that results from placing a transition metal ion in the crystal field generated by a set of ligands. It arises due to the fact that when the d orbitals are split in a ligand field, some of them become lower in energy than before. For example, in the case of an octahedron, the t2g set becomes lower in energy. As a result, if there are any electrons occupying these orbitals, the metal ion is more stable in the ligand field by the amount known as the CFSE. Conversely, the eg orbitals are higher in energy. So, putting electrons in them reduces the amount of CFSE.

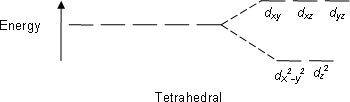
Q-Explain the crystal field theory of tetrahedral complexes.
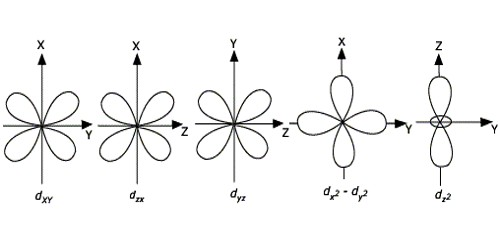
dxy dxz dyz
The electron density (i.e., the lobes of the orbitals) lies nearest to the point charges.
dx2-y2 dz2
The electron density lies further away from the point charges.
E.g; CH4
Q-Explain the d-orbital splitting of transition metal ions and the nature of ligands used.
CFT focuses on the interaction of the five (n − 1)d orbital’s with ligands arranged in a regular array around a transition-metal ion. Other common structures, such as square planar complexes, can be treated as a distortion of the octahedral model. According to CFT, an octahedral metal complex forms because of the electrostatic interaction of a positively charged metal ion with six negatively charged ligands or with the negative ends of dipoles associated with the six ligands. In addition, the ligands interact with one other electrostatically. According to VSEPR theory the lowest-energy arrangement of six identical negative charges is an octahedron, which minimizes repulsive interactions between the ligands.
The energies of the d-orbital of a transition-metal ion are affected by an octahedral arrangement of six negative charges. The five d-orbital are initially degenerate. On the distribution of six negative charges uniformly over the surface of a sphere, the d-orbital remain degenerate, but their energy will be higher due to repulsive electrostatic interactions between the spherical shell of negative charge and electrons in the d-orbital. Placing the six negative charges at the vertices of an octahedron does not change the average energy of the d-orbital, but it does remove their degeneracy: the five d-orbital split into two groups whose energies depend on their orientations. The dz2 and dx2−y2 orbital point directly at the six negative charges located on the x, y, and z axes. Consequently, the energy of an electron in these two orbital will be greater than it will be for a spherical distribution of negative charge because of increased electrostatic repulsions. In contrast, the other three d orbital (dxy, dxz, and dyz, collectively called the t2g orbitals) are all oriented at a 45° angle to the coordinate axes, so they point between the six negative charges. The energy of an electron in any of these three orbital is lower than the energy for a spherical distribution of negative charge.
The Nature of the Ligands
The Δo observed for a series of complexes of the same metal ion depends strongly on the nature of the ligands. For a series of chemically similar ligands, the magnitude of Δo decreases as the size of the donor atom increases. E.g.: Δo values for halide complexes generally decrease in the order F− > Cl− > Br− > I−. In addition, a small neutral ligand with a highly localized lone pair, such as NH3, results in significantly larger Δo values that might be expected. Because of the lone pair points directly at the metal ion, the electron density along the M–L axis is greater than for a spherical anion such as F−. The experimentally observed order of the crystal field splitting energies produced by different ligands is called the spectro-chemical series, shown here in order of decreasing Δo:
CO≈CN−> NO−2>en>NH3>SCN−>H2O>oxalate2− >OH−>F>acetate−>Cl−>Br−>I−
Q-Find the crystal field stabilization energy (CFSE) (in kJ/mol) for complex, [Ti(H2O)6]3+. According to CFT, the first absorption maximum is obtained at 20,3000 cm−1 for the transition.
ΔE=hcv−34
=6.63×10 Js × 3.00×108 m/s × 20300cm−1 × 1m100cm
=4.037×10−19J
This is energy change for one ion
For one mole
ΔE=4.037×10−19 J/ion × 6.02 × 1023 ions/mol
=243067J/mol
But, 1kJ=1000J
∴ΔE=243kJ/mol
But, T1 ion has d' electron configuration
CFSE=0.4ΔE
QCalculate the octahedral crystal field splitting energy in kJ/mol for [Fe(CN)6] 4- , if the wavelength of the most intensely absorbed light is 305 nm.
Δo = hν ν = c/λ Δo = hc/λ
Δo = 6.6261 x 10-34 Js (2.9979 x 108 m/s)/ 305 x 10-9 m
6.513 x 10-19 J x 1 kJ/1000J x 6.02214 x 1023 molecules /mol= 392 kJ/mol
Q-Calculate the crystal field stabilization energy (CFSE) for high spin Fe2+. Do not include pairing energy.
CFSE = 4(-2/5 Δo) + 2(+3/5 Δo)
= -2/5 Δo