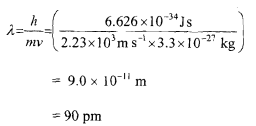Question Bank
Unit 06
Question Bank
Unit 06
Question Bank
Unit 06
Question Bank
Unit 06
Q-Discuss about the classical plane wave equation.
Classical Plane Wave Equation
A wave is a disturbance of a physical quantity undergoing simple harmonic motion or oscillations about its place. The disturbance gets passed on to its neighbors in a sinusoidal form.
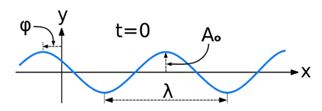
The equation for the wave is a second-order partial differential equation of a scalar variable in terms of one or more space variable and time variable. The one-dimensional wave equation is-
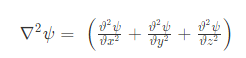
The amplitude (y) for example of a plane progressive sinusoidal wave is given by:
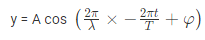
Where, A is the maximum amplitude, T is the period and φ is the phase difference of the wave if any and t is the time in seconds. For a standing wave-
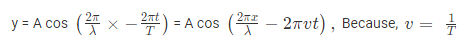
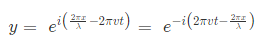
Q-Enlist the importance of schrodinger wave equation.
Importance of Schrodinger wave equation:
- The electronic structure of atoms and molecules can be well explained using the Schrodinger’s equation
- The solution of Schrodinger’s equation results in quantized properties of systems. E.g.: energy quantization. The quantization is a consequence of the periodic boundary conditions involved.
- Solving the Schrodinger’s equation for a solid is basically a many-body problem and it involves the solution of complex differential equations. The problem can be solved by expressing the differential Schrodinger’s equation in momentum space/reciprocal space, where the Schrodinger’s equation can be expressed as a set of linear algebraic equations rather than complex differential equations. Those linear equations can be solved using available computational numerical techniques accurately to predict the ground state properties of solids
- The solution of the Schrodinger’s equation in the reciprocal space gives the electronic band structure of solids.
Q-What is the application of hydrogen atom in schrodinger wave equation?
The wave function of an electron of hydrogen atom is calculated by the help of Schrodinger equation. The interaction between the particles is governed by charges and by the ignorance of electrostatic repulsion.
Time-independent Schrodinger equation:
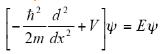
Here,
Total energy =Kinetic Energy +Potential energy
In order to attain the kinetic energy for the electron, the equation for centripetal force and coulomb is taken in consideration:
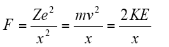
Here,
X= position of electron relative to the proton.
Hence the kinetic energy is given by-
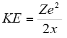
For the potential energy-
Potential Energy=work done to move charge from infinity to the orbital radius
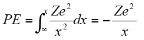
The total energy E is given by
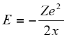
On substituting the values for total and potential energy and on rearrangement:
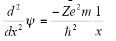
The original wave function is:
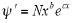
On differentiating the above equation we get-
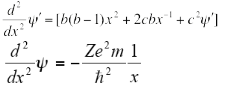
On equating the coefficients we get:
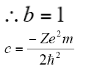
Therefore, the wave function of an electron of a hydrogen atom is:
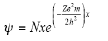
Q- Explain the differences in the use of the time dependent Schrodinger equation and the time-independent Schrodinger equation.
The time independent Schrodinger equation for a particle of mass m moving in one dimension with energy E in a system that does not change with time. The factor U is the potential energy of the particle at the point x, because the total energy E is the sum of potential and kinetic energy of the particle. The potential energy term does not depend on the time. But on the time dependent Schrodinger equation, The potential energy depends on space and time.
Q-How Schrodinger Equation reduces to the Newton’s? Explain.
Newton's equation describes a physical system and can predict how this changes with a set of initial conditions, we can solve for the force, mass and acceleration given enough information.
The Schrodinger equation also describes a physical system where we solve for the azimuth, polar and radial points of a spherical coordinate system. The difficulty mostly is in the conversion from Cartesian coordinates to spherical coordinates within the second-order partial derivatives.
The three solution equations of the spherical coordinate system are then applied to the spherical coordinate space with the quantum numbers n, l, m and s. These equations and quantum conditions describe the orbital shape of the system. For instance the most simple system is that of the hydrogen atom and therefore its orbital shape of the electron, knowing it has one electron and one proton.
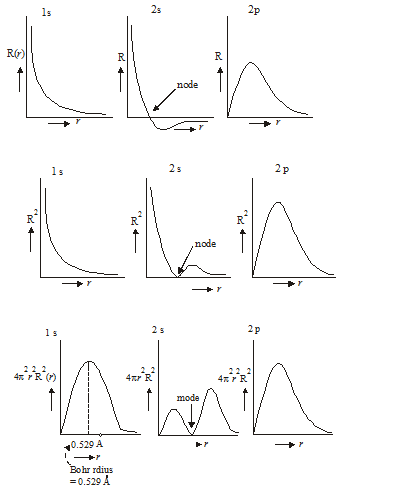
Q-Discuss about the wave mechanical model with graphical representation.
Electrons race around a central nucleus at such high speeds that they act like waves of energy. As electrons push each other around, the electron orbital clouds form different shapes. Scientists propose that atoms can have up to seven principle energy levels of electrons around the nucleus. This is the electron configuration for the element sulfur, which has 16 electrons.
We and everything around us are made of tiny groups of particles, called atoms. While atoms were once thought to be the smallest unit of matter, they are actually made up of much tinier, high-energy, negatively-charged particles circling at a crazy pace around a nucleus of positive and neutral particles. Since the outer-shell (valence) electrons control the chemical properties of a material, it would be useful to understand how they behave.
One popular theory is the wave-mechanical model, which proposes that electrons are almost as much like a wave of energy as they are like particles. They're moving so fast that they're not really in any one place at any given time, and they keep changing their path in response to the fields around them. In this lesson, we will discuss how scientists use the wave-mechanical model to describe the construction of an atom. The wave-mechanical model was proposed in the 1920s when scientists Erwin Schrödinger and Louis Victor de Broglie determined that the previous model (the Bohr model) was not useful for determining electron locations. The wave-mechanical theory proposes that each electron circling an atom's nucleus occupies a specific orbital and spins a certain direction, but the orbital is like a cloud or wave of energy, not the ring you might imagine thinking about the earth's orbit around the sun.
Q-Calculate the de Broglie wavelength associated with a cricket ball weighing 160 g thrown at a speed of 160 km per hour.
Mass of the cricket ball = 160 g = 160 x 10-' kg
= 0.16 kg
Velocity = 160 km/hr
= (160 x 1000)/3600 = 44.44 m s-'
The wavelength associated with the cricket ball will be
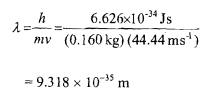
Let us take the velocity of the hydrogen molecule to be equal to its root mean square velocity V, = (~RTIM)"
Substituting the values of R, T and M, we get
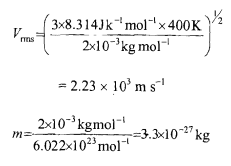
The associated wavelength will be