UNIT – 4

General System of Forces

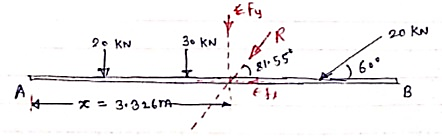
Question1) Determine the resultant of the system of forces acting on a beam as shown in figure.

Above Force system is Non concurrent force system.

Resolving the forces horizontally,

∑ Fx = - 20 Cos 60 = - 10 KN = 10 KN (towardleft)

Resolving forces vertically,

∑Fy = - 20 – 30 – 20 Sin 60

           = - 67.32 KN

∑Fy = 67.32 KN (downwards)

Resultant, R = √ (∑ Fx) 2 + (∑Fy) 2 = √10 2 + 67.322

R = 68.06 KN

Direction of Resultant,

tanα =   ∑Fy / ∑ Fx = 67.32 / 10.00

α = 81.550

Now taking moment about point A & using Varignon’s theorem.

∑MA = Moment of resultant A

(20 x 1.5) + (30 x 3) + (20 Sin 60 x 6) = (∑ Fx x 0 ) + (∑Fyx X)

223.92 = 67.32 x X

X = 223.92 / 67.32 = 3.326 m from point A

Ans

Question 2) For a given force system, find the resultant in magnitude & direction. Also find the location of Resultant.

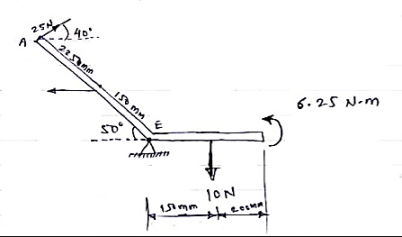
Answer) 

Resolving forces horizontally,

∑ Fx = - 15 + 25 Cos 40 = 4.15 N (toward right)

Resolving forces vertically,

∑Fy = 25 Sin 40 – 10

       = 6.07 n (upward)

R = √(∑ Fx) 2 + (∑Fy)2

= √4.152 + 6.072

R = 7.35 N

tanα =   ∑Fy / ∑ Fx = 6.07 / 4.15

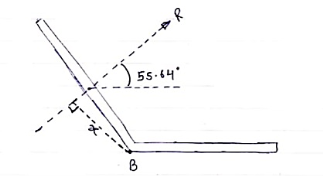
α= 55.640    - - -   Angle made by resultant 

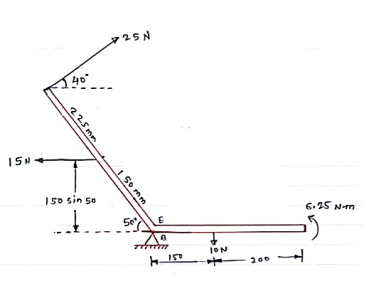
Question 3) To find exact position of R, let x is the perpendicular distance betn R & point B.

Answer 3)  Using Varignon’s theorem at point B.

R x X = ∑MB

          = (10 x 150) – (15 x 150 Sin 50) + ( 25 x 375 ) – ( 6.25 x 1000 )

= 1500 – 1723.6 + 9375 – 6250

= 2901.4 N.mm       (clockwise)

      x = 2901.4 / R

         = 2901.4 / 7.35

      x = 394.75 mm       from point B.

Question 3) Find resultant moment of two couples for the loading as shown in Fig

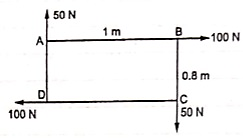
Answer 3) Moment of 50 N couple is clockwise,

= 50 x 1

= 50 N.m

Moment of 100 N couple is also clockwise

= 100 x 0.8 = 80 N.m.

Resultant Moment = 50 + 80 = 130 N.m

Question 4) Find the resultant and its point of application on y – axis for the force system acting on Triangular plate as shown in fig.

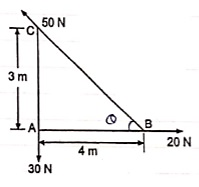
Answer 4)

θ = tan-1 (3/4)

   = 36.860 with Horizontal

Resolving forces in x & y dirn

∑ Fx = 20 – 50 Cosθ

         = 20 – 50 Cos 36.86

         = - 20 N

         = 20 N

∑Fy = - 30 + 50 Sin 36.86

       = 0.00007

       ≈ 0

R = √(∑ Fx) 2 + (∑Fy)2

         = 20 N toward left (as ∑ Fy = 0 )

Let us apply Varignon theorem at point B

∑MB = R.x

( 30 x 4 ) = Rx

Rx = -120 N.m = 120 N.m

As moment of Resultant is negative i.e. it is anticlockwise

-Rx = -120

X = -120 / -20 = 6 m

X = 6 m from point B and it will be above point. B to create anticlockwise moment.

Question 5) If the resultant moment about point A is 4800 Nm clockwise, determine the magnitude of F3 if F1 = 300 N and F2 = 400 N.

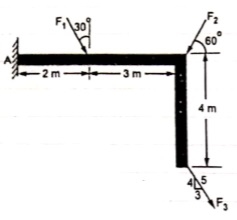
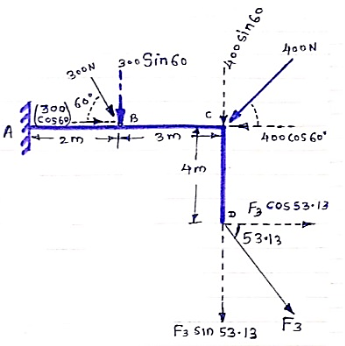Answer 5): Resultant Moment = 4800 N.m

Let us apply Varignon’s theorem at point A,

∑MB = (R.x )

[(300 60) x 2] + [(400 Sin 60) x 5] + [(F3 Sin 53.13 x 5)] – [(F3 Cos 53.13) x 4] = 4800

519.62 + 1732.05 + 3.99 F3 – 2.4 F3 = 4800

2251.67 + 1.59F3 = 4800

1.59 F3 = 2548.33

F3 = 2548.33 / 1.59      F3 = 2548.33 / 1.6

OR

F3 = 1602.72 NF3 = 1592.7 N

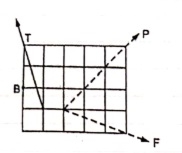
Question 6) The three forces shown in Fig. Create a vertical resultant acting through point B. If P = 361 N, compare the values of T and F.

Answer 6) From given figure,

1>. Angle made by Force P is, = tan-1 (3/3) = 450 with Horizontal

2>. Angle made by Force F is, = tan-1 (1/3) = 18.430 with Horizontal

3>. Angle made by Force T is, = tan-1 (3/1) = 71.560 with Horizontal

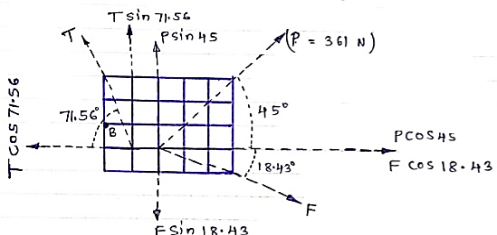
Resolving forces along x & y dirn,

As Resultant is vertical, let it is upward, then

∑ Fx = 0& ∑Fy = R

∑ Fx = P Cos 45 + F Cos 18.43 – T Cos 71.56

     0 = 361 Cos 45 + F Cos 18.43 – T Cos 71.56

     0 = 255.26 + 0.95 F – 0.32 T

0.95 F – 0.32 T = - 255.26   . . . . (1)

∑Fy = P Sin 45 – F Sin 18.43 + T Sin 71.56

      R = 361 Sin 45 – F Sin 18.43 + T Sin 71.56

  R = 255.26 – 0.32 F + 0.95 T …… (2)

Now as it is given that Resultant acts at point B, let us apply Varignon’s theorem at point B.

∑MB = R.x

But as R is acting at B point, its perpendicular distance from point B itself will be zero.             

∑MB = R.x

(P Cos 45 x 1) – (P Sin 45 x 2) + (T Cos 71.56 x 1) – (T Sin 71.56 x 1) – (F Cos 18.43 x 1) + (F Sin 18.43 x 2) = R x 0

As P = 361 N

-255.26 – (255.26 x 2) + 0.32 T – 0.95 T – 0.95 F + (0.32 F x 2) = 0

-765.78 + 0.32 T – 0.95 T – 0.95 F + 0.64 F = 0

-765.78 – 0.63 T – 0.31 F = 0

– 0.31 F – 0.63 T = 765.78 . . . . (3)

Solving eqn (1) and (3) simultaneously

0.95 F – 0.32 T = - 255.26

-0.31 F – 0.63 T = 765.78

F = -581.716 N      &

T = -929.282 N

Question 7) Determine the resultant of four forces tangent to the circle of radius 1.5 m as shown. Determine its location w.r.t.  ‘O’.

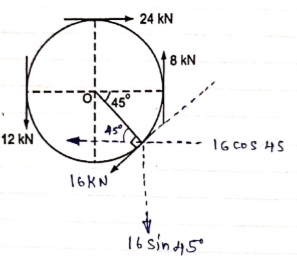
Answer 7) Resolving forces in X and Y direction,

∑ Fx = 24 - 16 Cos 45

        = 12.69 KN (  )

∑Fy = -12 + 8 – 16 Sin 45

       = -15.31 kN

       = 15.31 kN (  )

Resultant R = √(∑ Fx) 2 + (∑Fy)2

                     = √ 12.69 2 + (-15.31)2

                 R = 19.88 kN

Direction of Resultant,

α =   tan-1(∑Fy / ∑ Fx)

α =   tan-1(15.31 / 12.69)

α =   50.350in 4th quadrant

To know exact location of Resultant, let us apply Varignon’s theorem at point O.

∑MO = R.x

-(12 x 1.5) + (24 x 1.5) – (8 x 1.5) + (16 x 1.5) = (19.88 x X)

30 = R.x

As product of R.x is positive it means moment of Resultant is positive. To create positive clockwise moment of Resultant it must be acting on Right side of O (in 4th quadrant).

30 = 19.88 x X

X = 1.51 m from O on the right hand side.

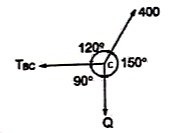
Question 8) Find the axial force in the bar AB & AC as shown in figure.

Consider the free body diagram of all forces at B.

Answer 8)

Q1 = tan -1 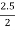  = 51.34º

Q2 = tan-1 = 45º

Let the forces developed in the member AB & AC are FAB &FBCrespectively. The force diagram will be as follows at B.

Applying Lami’s Theorem:

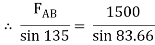
FAB = 1067.19 N

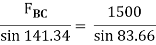
FBC = 942.81 N

Question 9) Find the tensions in the string AB, BC, CD, DE of the given system as shown in figure. String BC is horizontal & pulley D is frictionless.

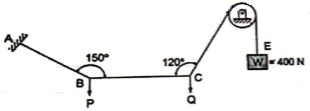
Answer 9)

The string passes over the pulley & is attached to weight w = 400 N.  

Thus TCD = TDE = 400 N

Consider joint C & apply Lami’s theorem

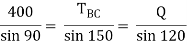
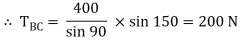
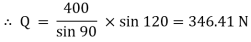
Now consider FBD at joint B

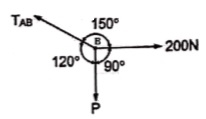
By using Lami’s theorem

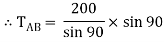
TAB = 230.94 N

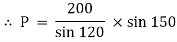
Question 10) Two identical spheres having weight 1000 N are kept in a container as shown in figure. Find the reaction at all contact surfaces.

Answer 10)

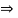Consider the free body diagram of sphere B as shown below:

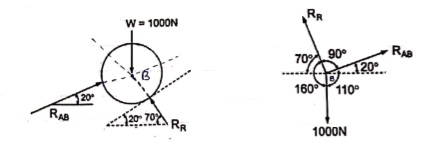
By lami’s theorem

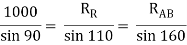
RRR = 939.69 N

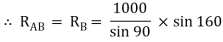
  = RAB

Now consider FBD of sphere A

∑Fx = 0

-RB cos 20 – RQ cos 70 + Rp = 0

-342.02 cos 20 – RQ sin 70 + Rp  = 0

Rp = 321.39 + 0.34 RQ          ------------------(1)

∑ fy = 0

RQ sin 70 – 342.02 sin 20 – 1000 = 0

RQ = 1188.66 N    - put in equation (1)

Rp = 725.5 N

Question 11) Two members AB & BC are supporting a load of 200 kN as shown in figure. Find the forces developed in the members AB & BC

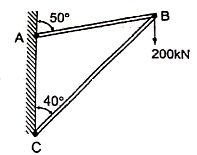
Answer 11)

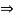Consider the free body diagram of joint B as shown in figure

Assume that member BC is in compression & AB is in tension. By using Lami’s theorem at B,

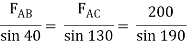
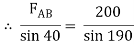
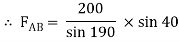
FAB = -740.33 kN 

-ve sign indicates that member AB is not in Tension but is in compression.

Now,

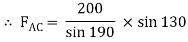
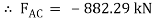
-ve sign indicates that member BC is not in compression but in tension.