UNIT-1

UNIT-1

Q 1: Solve the following improper Integral 

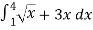
Solution:

Given,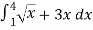

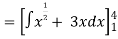
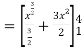
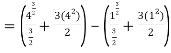
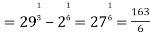
Q2:  Solve the following improper Integral

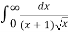
Solution: Given,

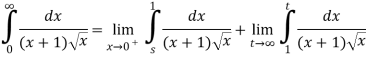
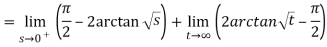
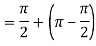
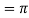
Q3:  Solve the following improper Integral

Solution: Given,

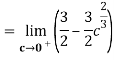
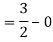
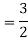
Q 4  :  Solve the following improper Integral

Solution: Given,

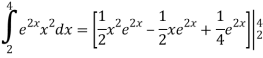
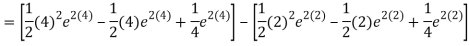
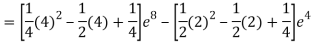
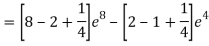
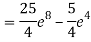
Q 5: evaluate the integral

Solution: we use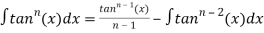

Substituting a=2x

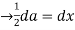
Hence,

              =

              =

             =

              =

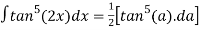
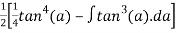
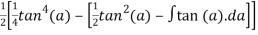
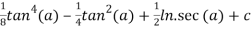
Q 6: Evaluate the integral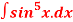

Solution: we use the formula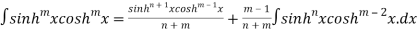

                   =

                   = .

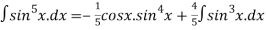
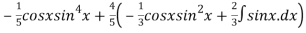
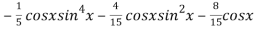Q 7: f(B) =      Solve the given function.

Solution:    =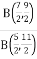 

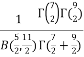
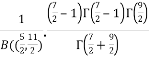       =             [Recursive function for the gamma function]

       =       [Recursive formula for the gamma function]

       =

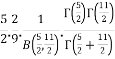
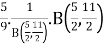        =     [By the definition of Beta function]

       =

Q 8:

B  =

               = 

                =

              =

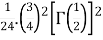
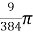         =    [because ]

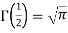Q 9: Find the area of the surface generated by rotating the function about the x-axis over

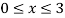  and the curve

Solution: we have the equation of the form y=f(x) and we are rotating around the x-axis, we’ll  use the formula

S =

We will calculate 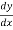and then substitute it back into the equation

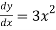
S =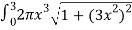

S =

Using u-substitution and setting u= 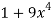and du=36x3dx,

We calculate

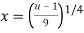
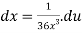
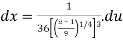
Plugging these values back into the integral we get,

S=

S =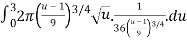

S =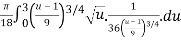

S =

By integration we get

S =

S =

We wil insert back for u, and we have u = 1+9x4, and then evaluate over the interval

S =

=

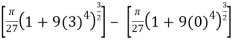
S = 2, 294.8 square units.

THEREFORE,

The surface area obtained by rotating y= x3 around the x-axis over the interval 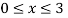is S = 2, 294.8

Q 10: Find the volume generated by revolving the region bounded by y = x2 and the x-axis on [-2,3] about the x-axis

Solution: The volume(v) of the solid is

V =

    =

    =

    =

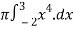
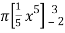
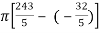
V = 55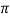

UNIT-1

Q 1: Solve the following improper Integral 

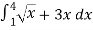
Solution:

Given,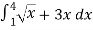

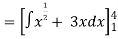
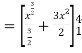
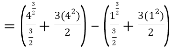
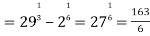
Q2:  Solve the following improper Integral

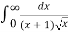
Solution: Given,

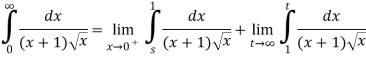
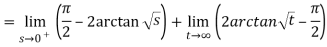
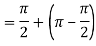
Q3:  Solve the following improper Integral

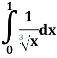
Solution: Given,

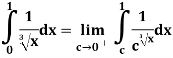
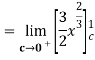
Q 4  :  Solve the following improper Integral

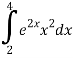
Solution: Given,

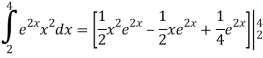
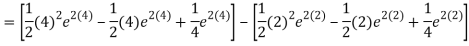
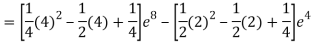
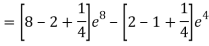
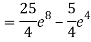
Q 5: evaluate the integral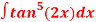

Solution: we use

Substituting a=2x

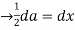
Hence,

              =

              =

             =

              =

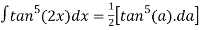
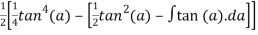
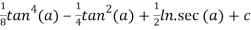
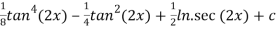
Q 6: Evaluate the integral

Solution: we use the formula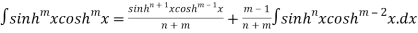

                   =

                   = .

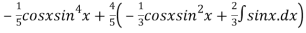
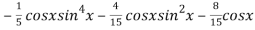Q 7: f(B) =      Solve the given function.

Solution:    = 

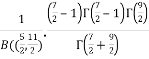       =             [Recursive function for the gamma function]

       =       [Recursive formula for the gamma function]

       =

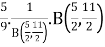        =     [By the definition of Beta function]

       =

Q 8:

B  =

               = 

                =

              =

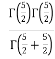
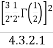
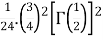
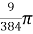         =    [because ]

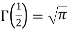Q 9: Find the area of the surface generated by rotating the function about the x-axis over

  and the curve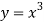

Solution: we have the equation of the form y=f(x) and we are rotating around the x-axis, we’ll  use the formula

S =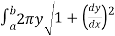

We will calculate 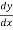and then substitute it back into the equation

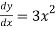
S =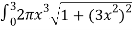

S =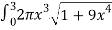

Using u-substitution and setting u= 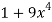and du=36x3dx,

We calculate

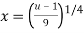
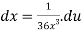
Plugging these values back into the integral we get,

S=

S =

S =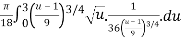

S =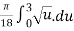

By integration we get

S =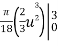

S =

We wil insert back for u, and we have u = 1+9x4, and then evaluate over the interval

S =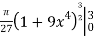

=

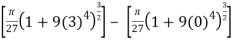
S = 2, 294.8 square units.

THEREFORE,

The surface area obtained by rotating y= x3 around the x-axis over the interval is S = 2, 294.8

Q 10: Find the volume generated by revolving the region bounded by y = x2 and the x-axis on [-2,3] about the x-axis

Solution: The volume(v) of the solid is

V =

    =

    =

    =

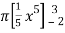
V = 55