UNIT 2

Q:1  Solve the given  graph by Rolle’s theorem

Solution: Given and

f(1) =f(5) =-1

Since by Rolle’s theorem, there exists at least one value of x=0 such that 

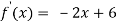
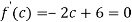
Solve the above equation to obtain

C=3

Therefore at x=3 there is a tangent to the graph of f that has a slope equal to zero (horizontal line ) as shown in figure below.

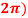Q:2     Solve the given graph by Rolle’s theorem                                                  is shown below .f(0)=f(=2 and f is continous on and differentiable on (0,

Solution: Given 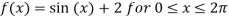and f(0)=f(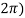=2

Since by Rolle’s theorem, there exists at least one value of x=c such that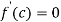 

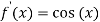
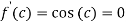
The above equation has two solutions on the interval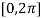

Therefore both at x= and x=3 there are tangents to the graph that have a slope equal to zero (horizontal line ) as shown in figure  below.

Q: 3: Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in

Solution: Here f(x) = ex(sin x – cos x);

i)      Ex is an exponential function continuous for every also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in 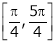and Hence ex(sin x – cos x) is continuous in .

Ii)    Consider

f(x) = ex(sin x – cos x)

Diff. w.r.t. x we get

f’(x) = ex(cos x + sin x) + ex(sin x + cos x)

   = ex[2sin x]

Clearly f’(x) is exist for each 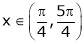& f’(x) is not infinite.

Hence f(x) is differentiable in .

Iii)  Consider

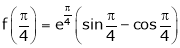
Also,

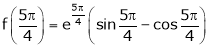
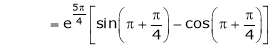
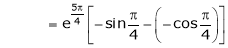
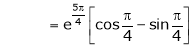
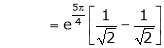
Thus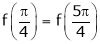

Hence all the conditions of Rolle’s theorem are satisfied, so there exist 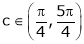such, that

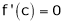
i.e.

i.e. sin c = 0

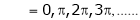
But

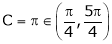
Hence Rolle’s theorem is verified.

Q:4  Use LaGrange’s mean value theorem to determine a point P on the curve y=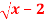

Where the tangent is parallel to the chord joining (2,0) and (3,1)

Solution: Consider y= 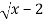in [2,3]

(i)                Function is continuous in[2,3] as  algebraic expression with positive exponent is continuous.

(ii)              y’= 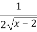,  y’ exists in (2,3) hence the function is derivable in (2,3)

Hence the condition of LMV theorem is satisfied.

Hence, there exists one c in (2,3) such that =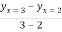

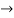
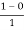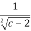
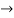  = 4(c-2) = 1 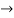4c=9 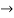 c= 4/9

for x = 9/4, tangent is parallel to the chord joining (2,0) and (3,1)

Substituting in (i) we get,

Y= 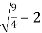  = 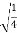= ½

Q: 5: Verify lagrange’s mean value theorem for the following function

f(x) =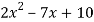

Putting x=a=2 and x=b=5 ,we get

f(2) =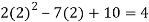

f(5) =

Clearly,

f(2) f(5)

Since f(x) is a polynomial function in x, then f(x) is continuous in [2,5].

And f(x) is polynomial in x ,then it can be differentiate such that f’(x) = 4x-7

Then by LMV theorem there exists c 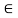(2,5) such that’

f’ (c) =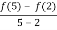

4c-7 =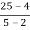

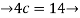c=3.75

Hence lagrange’s mean value theorem is verified for f(x) in [2,5].

Q:6: Verify the Lagrange’s mean value theorem for

Solution: Here f(x) = logx  and x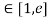

i)      Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]

Ii)    Consider f(x) = log x.

Diff. w.r.to, x we get,

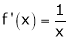
Clearly f’(x) exists for each value of x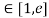 & is finite.

Hence all conditions of LMVT are satisfied Hence at least c

Such that

i.e.

i.e.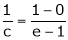

i.e.

i.e.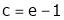

Since e = 2.7183

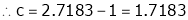
Clearly c = 1.7183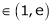

Hence LMVT is verified.

Q: 7: Verify mean value theorem for f(x) = tan-1x in [0, 1]

Solution: Here ;

i)      Clearly 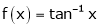is an inverse trigonometric function and hence it is continuous in [0, 1]

Ii)    Consider

Diff. w.r.t. x we get,

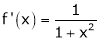
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite

Hence all conditions of LMVT are satisfied, Thus there exist

Such that

i.e.

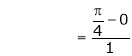
i.e.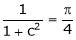

i.e.

i.e.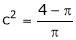

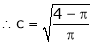
Clearly

Hence LMVT is verified.

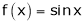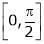Q:8: Verify Cauchy mean value theorems for &in Solution :Let &;

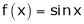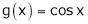i)      Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in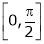

Ii)    Since &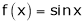

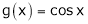
Diff. w.r.t. x we get,

&

Clearly both f’(x) and g’(x) exist & finite in . Hence f(x) and g(x) is derivable in and

Iii)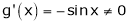 

Hence by Cauchy mean value theorem, there exist at least 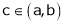such that

i.e.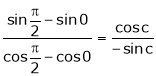

i.e. 1 = cot c

i.e.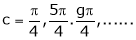

Clearly

Hence Cauchy mean value theorem is verified.

Q:9 : Considering the functions ex an e-x, show that c is arithmetic mean of a & b.

Solution: Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b].

i)      Consider &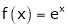

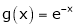
Diff. w.r.t. x we get

and

Clearly f(x) and g(x) are derivable in (a, b)

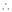By Cauchy’s mean value theorem 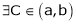such that

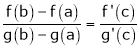
i.e.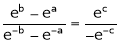

i.e.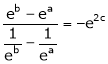

i.e.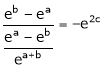

i.e.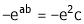

i.e.

i.e.

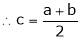
Thus

i.e. c is arithmetic mean of a & b.

Hence the result

Q:10:

Find the Taylor series for the following:

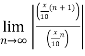= <1

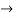(X/10)<1 and (x/10) > -1

Therefore radius of convergence is (-10,10)

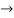  ROC =10

Example 2:

f(n)5 =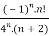

Here the ROC is 4

Q:11Compute the Taylor series centered at zero for f(x)= sinx

Solution:

f(x)=sinx               f(0)=0

f’(x) =cosx             f’(0)=1

f’’(x)=-sinx           f’’(0)=0

f’’’(x) = -cosx       f’’’(0)=-1

f(4)(x)= cosx        f(4) (0)= 1

Applying Taylor series we get

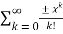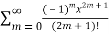T(x) =   =   = x-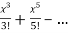

Thus turns out to converge x to sinx.

Maclaurian series:

Q:12 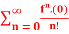  (x)n

Solution:

f(x)=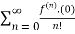

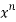
    = f(0)+f’(0)x+ x2 + 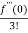x3 +......

    = 1+x+x2 +x3 + .....

=

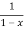
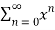
Q:13: Find the Maclaurian series for f(x)= ex

Solution:

To get Maclaurian series, we look at the Taylor series polynomials for f near 0 and let them keep going.

Considering for example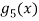

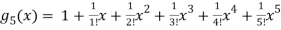
By Maclaurian series we get,

+

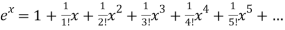Q:14

Find out the maxima and minima of the function

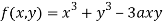
Solution:

   Given 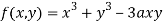    …(i)

         Partially differentiating (i) with respect to x we get

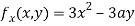    ….(ii)

         Partially differentiating (i) with respect to y we get

    ….(iii)

          Now, form the equations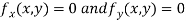

                    Using (ii) and (iii) we get

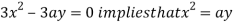
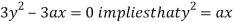
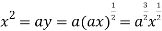          using above two equations

                     Squaring both side we get

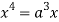
                      Or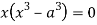 

                       This show that

                         Also we get

                 Thus we get the pair of value as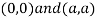

                  Now, we calculate

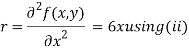
      Putting above values in

      At point (0,0)  we get

      So, the point (0,0) is a saddle point.

      At point 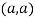we get

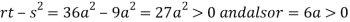
        So the point is the minimum point where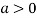

          In case 

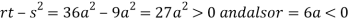
         So the point is the maximum point where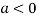

Q:15

Find the maximum and minimum point of the function

        Partially differentiating given equation with respect to and x and y then equate them to zero                 

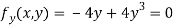
       On solving above we get 

         Also

            Thus we get the pair of values (0,0), (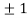,0) and (0,

        Now, we calculate

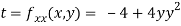
        At the point (0,0)

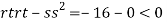
       So function has saddle point at (0,0).

       At the point (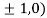

         So the function has maxima at this point (.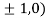

        At the point (0,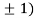

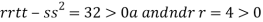
       So the function has minima at this point (0,.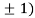

        At the point (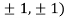

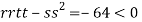
        So the function has an saddle point at (

Q:16 Find the maximum and minimum value of

Let

Partially differentiating given function with respect to x and y and equate it to zero

  ..(i)

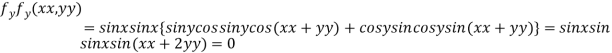    ..(ii)

      On solving (i) and (ii) we get

Thus pair of values are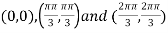

Now, we calculate

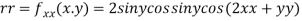
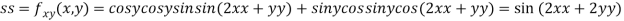
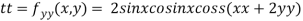
At the point (0,0)

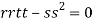
  So further investigation is required

On the x  axis y  = 0  , f(x,0)=0

On the line y=x,

At the point

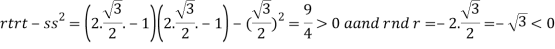
So that the given function has maximum value at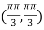

Therefore maximum value of given function

At the point

So that the given function has minimum value at

Therefore minimum value of the given function

Q:17: Evaluate 

Solution:

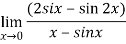
Differentiate the above form ,we get

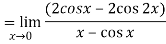
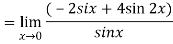
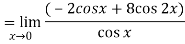
Now substitute the limit,

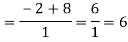
Therefore ,

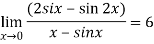
Q:18: Evaluate

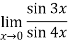
Given,

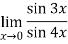
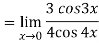
Now substitute the limit

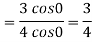
Therefore ,