Unit 1
Introduction to Mechanics
Question 1) Explain engineering mechanics.
Answer:
Mechanics is the physical science concerned with the behaviour of bodies that are acted upon by forces. Mechanics is a branch of the physical sciences concerned with the state of rest or motion of bodies that are subjected to the action of forces. The study of mechanics involves many more subject areas. However, initial study is usually split into two areas; statics and dynamics.
Statics is concerned with bodies that are either at rest or move with a constant speed in a fixed direction. Dynamics deals with the accelerated motion of bodies. Statics can therefore be considered as a special case of dynamics where the acceleration is zero. In engineering, since many objects are designed with the intention that they are at rest or their motion remains constant, statics deserves special treatment.
Question 2) Explain Idealisations of mechanics.
Answer:
In mechanics we look at real life situations and try to predict what will happen. The problem with real life is that it is often quite complicated. When studying problems in mechanics we often make idealisations of real life situations that simplify the problem. There are many commonly used idealisations that we will introduce in later sheets. Here follows a list of some common idealisations that are used in mechanics.
Particles are bodies which can be treated as a point mass in a given context. For example, when modelling the motion of the planets around the Sun, the planets and Sun can be treated as particles. Much of basic mechanics study is concerned with objects that can be treated as particles.
Connected particles arise in problems where two objects are attached in some way and both objects can be treated as particles. For example, two masses, connected by a string which passes over a pulley could be modelled as connected particles.
Rigid bodies can be considered as combinations of particles in which all the particles remain at a fixed distance from one another both before and after applying a force i.e. there is no bending or stretching. For example a brick can in most circumstances be thought of as a rigid body. Many real life objects can be considered to be rigid bodies to a good approximation.
Question 3) Explain Fundamental concept of mechanics.
Answer:
Certain concepts and definitions are basic to the study of mechanics and they should be understood at the outset. The basic concepts in mechanics are space, time, mass and force. These concepts cannot be truly defined. They should be accepted on the basis of our intuition and experience, and used as a mental frame of reference for our study of mechanics.
In Newtonian mechanics, space, time and mass are absolute quantities, which mean that they are independent of each other (this is not true in Relativistic Mechanics, where the time of an event depends upon its position and the mass of
a body varies with its velocity) and cannot be defined in terms of other quantities
Or in simpler terms. Force is a derived quantity.
Question 4) Explain ACTIONS AND EFFECTS OF FORCES?
Answer:
A force is defined as the action of a body on another body. A force is applied either through a direct contact or through a remote action. Forces applied through a remote action are gravitational, electrical, and magnetic forces. All other forces are applied through direct contacts.
Force acting on a body produces effects that can be divided into two types, namely external effect and internal effect.
As an illustration, consider the structure portrayed Assume that the structure is of negligible mass. The applied force F acting on the structure causes the reactive forces R1 and R2 which are applied by the support surfaces onto the structure so as to balance F. The reactions R1 and R2 are effects external to the body which are caused by F. Hence, external forces acting on a body are of two types, namely applied external forces (also called active forces) and reactive forces.
Besides causing the reactions R1 and R2, the applied force F also causes effects internal to the members of the structure. These effects are in the forms of stresses and strains that appear in the material of the structure. The effects exist to balance the respective external actions and effects.
In the study of mechanics, only the external effects of a force are considered. The internal effects are studied in disciplines of study specific to them, for example Mechanics of Materials (also known as Strength of Materials).
Question 5) Explain Characteristics of force.
Answer:
- Force can introduce motion in a body.
- Force can change direction of a moving body.
- Force can change size of an object.
- Force is a vector quantity.
- Force can stop a moving body.
- Force has a unit of Newton (N) in M.K.S system and dyne in C.G.S system.
- They are of two types: contact and non-contact forces.
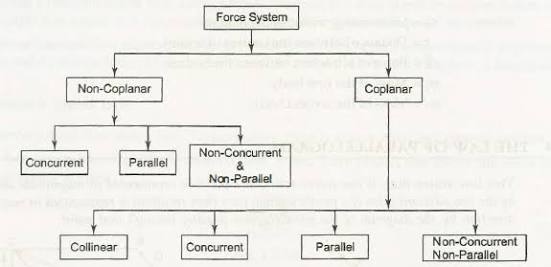
Force system is a collection of forces acting at specified locations.
Different types of force system:
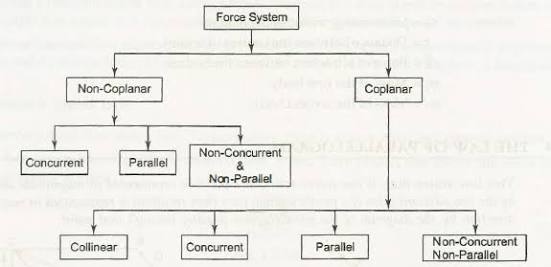
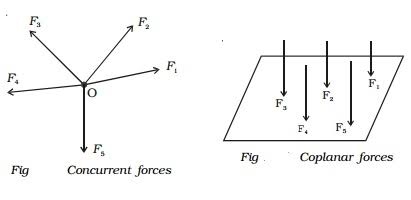
(i) COPLANAR FORCES:
Forces acting on only one plane are known as coplanar force system.
Or, we can say that if the effect of forces is only in one plane of object then the force system is known as coplanar force.
Ii) CONCURRENT FORCES:
A concurrent coplanar force system is a system of two or more forces whose lines of action ALL intersect at a common point.
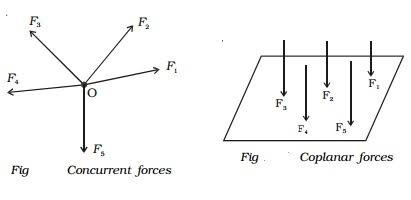
Iii) LIKE FORCES
Parallel coplanar force system consists of two or more forces whose lines of action are all parallel to one another.
Iv) UNLIKE FORCES:
If the parallel forces are such that their directions are opposite to each other, then they are termed as "UNLIKE FORCE".
Question 6) Explain equilibrant force.
Answer:
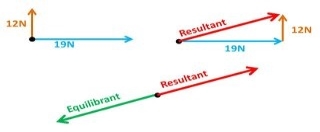
Equilibrant force is equal in magnitude but opposite in direction to the resultant force of all the forces acting on a body.
- Equilibrant force= - resultant force
- R=√[(a^2+b^2+2abcos@)]
- R=√[(60)^2+(40)^2)+2*60*40*cos(90°)]
- R=√5200
- R=72.112
If two forces are equal in opposite directions, each force is the equilibrant of the other. The equilibrant force is labelled as FQ is equal in magnitude but opposite in direction to the resultant vector. (FQ = -FR)
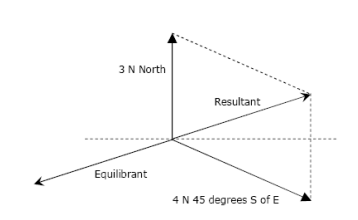
The equilibrant force is the single force that if applied at the same point (equal in magnitude and opposite on direction) that produces equilibrium.
Question 7) Explain Resultant force.
Answer:
Resultant force
When an object is subject to several forces, the resultant force is the force that alone produces the same acceleration as all those forces.
For example, if 4 forces act on a block and cause it to accelerate 1 m/s2 south, then the resultant force is the force that, if applied alone to the block, will also make it accelerate 1 m/s2 south.
The reason why the resultant force is useful is that it allows us to think about several forces as though they were a single force. This means that to determine the effect that several forces have on an object, we only need to determine the effect that a single force has.
If we know the mass m of an object and the acceleration a produced by the forces that act on it, we can find the resultant force using Newton's Second Law. Indeed, according to Newton's Second Law, the force F that alone produces the acceleration a on an object of mass m is:
F = ma
This force F is our resultant force. So, we can write:
R = ma
Which indicates that the resultant force R has the same direction as a, and has magnitude equal to the product ma.
For example, if a box of 1.5 kg is subject to 5 forces which make it accelerate 2.0 m/s2 north-west, then the resultant force is directed north-west and has the magnitude equal to 1.5 kg × 2.0 m/s2 = 3.0 N.
Often, however, we know the forces that act on an object and we need to find the resultant force. Experiments show that when an object is subject to several forces, F1, F2 the resultant force R is the vector sum of those forces:
R = F1 + F2 +…
Notice that this is not a mere sum of the magnitudes of the forces, but the sum of the forces taken as vectors, which is more involved because vectors have both a magnitude and a direction that we need to consider when doing the sum.
According to the above equation, if an object is subject to no forces, then the resultant force is zero, and if an object is subject to only one force, then the resultant force is equal to that force. These two cases are pretty simple, but what about an object subject to two or more forces.
To explain this clearly, we will now go through all the cases that can happen, from simple ones in which all the forces are parallel, to more complex ones in which the forces are not parallel, and show how to find the resultant force in each of them with the help of examples.
Question 8) Explain Resolution and composition of forces.
Answer:
Resolution of a Force
The process of substituting a force by its components so that the net effect on the body remains the same is known as resolution of a force.
- For each force, there exist an infinite number of possible sets of components.
Suppose a force is to be resolved into two components. Then:
- When one of the components is known, the second component can be obtained by applying the triangle rule.
- When the line of action of each component is known, the magnitude and the sense of the components are obtained by parallelogram law.
Question 9) Explain Principle of Resolution.
Answer:
The algebraic sum of the resolved parts of a number of forces in the given direction is equal to the resolved part of their resultant in the same direction.
Composition of Forces
The process of finding out the resultant force of a number of given forces is called the composition/compounding of forces.
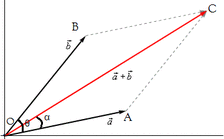
Parallelogram Law
"If two forces acting simultaneously on a particle is represented in magnitude and direction by two adjacent sides of a parallelogram, their resultant may be represented in magnitude and direction by the diagonal of the parallelogram which passes through the point of intersection."
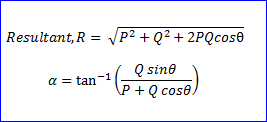
Question 10) Explain Force system.
Answer:
It is an external agency which produces or tends to produce, destroy or tends to destroy motion. OR
It is an external agent which changes or tends to change the state of motion of body.
It is a vector quantity.
Force is also known as rate of change of momentum.
As momentum = mass x velocity
But mass will never change, then
Force = mass x rate of change of velocity
= mass x Acceleration
F = P = ma
S.I. Unit: - Newton (N)
Kilo Newton (KN) = 103 N
Mega Newton (MN) = 106 N
Giga Newton (GN) = 103 N
Tera Newton (TN) = 1012 N
1 Kg Force:-
Force required producing unit gravitational acceleration on unit mass.
01 kg force = mass x Acceleration (gravity)
= 1 kg x 9.81 m / s2
= 9.81 kg.m / s2
1 kg.F = 9.81 Kg m / s2
1 kg.F = 9.81 N
I.e. 1 Kg = 9.81 N
Characteristics of Force:-
1. Magnitude: - The value of force i.e. 10N, 2KN, etc.
2. Direction:- Line of action & angle formed with fixed axis.
3. Nature of force or sense:-It means whether the force is push or pull.
Pull type force Push type force
Push: - Force acting towards the point
Pull: - Force acting away from the point.
4. Point of application:-
The point at which or through which the force acts.
Effects of Force:-
Force may produce following effects on the body.
1. It may change the state of body.
i.e. if body is at rest, force may bring it in motion or if body is in motion, force may accelerate it or force may stop it or may retard it.
2. It may produce internal stress in the body.
3. It may produce deformation in non-rigid body.
4. It may produce rotational effect in body.
5. It may keep the body in stable state (Equilibrium).
Unit 1
Introduction to Mechanics
Question 1) Explain engineering mechanics.
Answer:
Mechanics is the physical science concerned with the behaviour of bodies that are acted upon by forces. Mechanics is a branch of the physical sciences concerned with the state of rest or motion of bodies that are subjected to the action of forces. The study of mechanics involves many more subject areas. However, initial study is usually split into two areas; statics and dynamics.
Statics is concerned with bodies that are either at rest or move with a constant speed in a fixed direction. Dynamics deals with the accelerated motion of bodies. Statics can therefore be considered as a special case of dynamics where the acceleration is zero. In engineering, since many objects are designed with the intention that they are at rest or their motion remains constant, statics deserves special treatment.
Question 2) Explain Idealisations of mechanics.
Answer:
In mechanics we look at real life situations and try to predict what will happen. The problem with real life is that it is often quite complicated. When studying problems in mechanics we often make idealisations of real life situations that simplify the problem. There are many commonly used idealisations that we will introduce in later sheets. Here follows a list of some common idealisations that are used in mechanics.
Particles are bodies which can be treated as a point mass in a given context. For example, when modelling the motion of the planets around the Sun, the planets and Sun can be treated as particles. Much of basic mechanics study is concerned with objects that can be treated as particles.
Connected particles arise in problems where two objects are attached in some way and both objects can be treated as particles. For example, two masses, connected by a string which passes over a pulley could be modelled as connected particles.
Rigid bodies can be considered as combinations of particles in which all the particles remain at a fixed distance from one another both before and after applying a force i.e. there is no bending or stretching. For example a brick can in most circumstances be thought of as a rigid body. Many real life objects can be considered to be rigid bodies to a good approximation.
Question 3) Explain Fundamental concept of mechanics.
Answer:
Certain concepts and definitions are basic to the study of mechanics and they should be understood at the outset. The basic concepts in mechanics are space, time, mass and force. These concepts cannot be truly defined. They should be accepted on the basis of our intuition and experience, and used as a mental frame of reference for our study of mechanics.
In Newtonian mechanics, space, time and mass are absolute quantities, which mean that they are independent of each other (this is not true in Relativistic Mechanics, where the time of an event depends upon its position and the mass of
a body varies with its velocity) and cannot be defined in terms of other quantities
Or in simpler terms. Force is a derived quantity.
Question 4) Explain ACTIONS AND EFFECTS OF FORCES?
Answer:
A force is defined as the action of a body on another body. A force is applied either through a direct contact or through a remote action. Forces applied through a remote action are gravitational, electrical, and magnetic forces. All other forces are applied through direct contacts.
Force acting on a body produces effects that can be divided into two types, namely external effect and internal effect.
As an illustration, consider the structure portrayed Assume that the structure is of negligible mass. The applied force F acting on the structure causes the reactive forces R1 and R2 which are applied by the support surfaces onto the structure so as to balance F. The reactions R1 and R2 are effects external to the body which are caused by F. Hence, external forces acting on a body are of two types, namely applied external forces (also called active forces) and reactive forces.
Besides causing the reactions R1 and R2, the applied force F also causes effects internal to the members of the structure. These effects are in the forms of stresses and strains that appear in the material of the structure. The effects exist to balance the respective external actions and effects.
In the study of mechanics, only the external effects of a force are considered. The internal effects are studied in disciplines of study specific to them, for example Mechanics of Materials (also known as Strength of Materials).
Question 5) Explain Characteristics of force.
Answer:
- Force can introduce motion in a body.
- Force can change direction of a moving body.
- Force can change size of an object.
- Force is a vector quantity.
- Force can stop a moving body.
- Force has a unit of Newton (N) in M.K.S system and dyne in C.G.S system.
- They are of two types: contact and non-contact forces.
Force system is a collection of forces acting at specified locations.
Different types of force system:
(i) COPLANAR FORCES:
Forces acting on only one plane are known as coplanar force system.
Or, we can say that if the effect of forces is only in one plane of object then the force system is known as coplanar force.
Ii) CONCURRENT FORCES:
A concurrent coplanar force system is a system of two or more forces whose lines of action ALL intersect at a common point.
Iii) LIKE FORCES
Parallel coplanar force system consists of two or more forces whose lines of action are all parallel to one another.
Iv) UNLIKE FORCES:
If the parallel forces are such that their directions are opposite to each other, then they are termed as "UNLIKE FORCE".
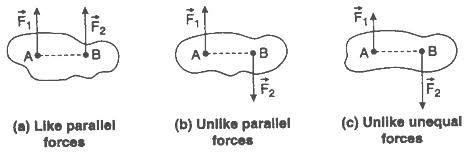
Question 6) Explain equilibrant force.
Answer:
Equilibrant force is equal in magnitude but opposite in direction to the resultant force of all the forces acting on a body.
- Equilibrant force= - resultant force
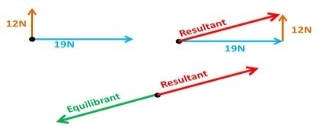
- R=√[(a^2+b^2+2abcos@)]
- R=√[(60)^2+(40)^2)+2*60*40*cos(90°)]
- R=√5200
- R=72.112
If two forces are equal in opposite directions, each force is the equilibrant of the other. The equilibrant force is labelled as FQ is equal in magnitude but opposite in direction to the resultant vector. (FQ = -FR)
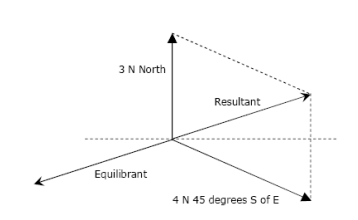
The equilibrant force is the single force that if applied at the same point (equal in magnitude and opposite on direction) that produces equilibrium.
Question 7) Explain Resultant force.
Answer:
Resultant force
When an object is subject to several forces, the resultant force is the force that alone produces the same acceleration as all those forces.
For example, if 4 forces act on a block and cause it to accelerate 1 m/s2 south, then the resultant force is the force that, if applied alone to the block, will also make it accelerate 1 m/s2 south.
The reason why the resultant force is useful is that it allows us to think about several forces as though they were a single force. This means that to determine the effect that several forces have on an object, we only need to determine the effect that a single force has.
If we know the mass m of an object and the acceleration a produced by the forces that act on it, we can find the resultant force using Newton's Second Law. Indeed, according to Newton's Second Law, the force F that alone produces the acceleration a on an object of mass m is:
F = ma
This force F is our resultant force. So, we can write:
R = ma
Which indicates that the resultant force R has the same direction as a, and has magnitude equal to the product ma.
For example, if a box of 1.5 kg is subject to 5 forces which make it accelerate 2.0 m/s2 north-west, then the resultant force is directed north-west and has the magnitude equal to 1.5 kg × 2.0 m/s2 = 3.0 N.
Often, however, we know the forces that act on an object and we need to find the resultant force. Experiments show that when an object is subject to several forces, F1, F2 the resultant force R is the vector sum of those forces:
R = F1 + F2 +…
Notice that this is not a mere sum of the magnitudes of the forces, but the sum of the forces taken as vectors, which is more involved because vectors have both a magnitude and a direction that we need to consider when doing the sum.
According to the above equation, if an object is subject to no forces, then the resultant force is zero, and if an object is subject to only one force, then the resultant force is equal to that force. These two cases are pretty simple, but what about an object subject to two or more forces.
To explain this clearly, we will now go through all the cases that can happen, from simple ones in which all the forces are parallel, to more complex ones in which the forces are not parallel, and show how to find the resultant force in each of them with the help of examples.
Question 8) Explain Resolution and composition of forces.
Answer:
Resolution of a Force
The process of substituting a force by its components so that the net effect on the body remains the same is known as resolution of a force.
- For each force, there exist an infinite number of possible sets of components.
Suppose a force is to be resolved into two components. Then:
- When one of the components is known, the second component can be obtained by applying the triangle rule.
- When the line of action of each component is known, the magnitude and the sense of the components are obtained by parallelogram law.
Question 9) Explain Principle of Resolution.
Answer:
The algebraic sum of the resolved parts of a number of forces in the given direction is equal to the resolved part of their resultant in the same direction.
Composition of Forces
The process of finding out the resultant force of a number of given forces is called the composition/compounding of forces.
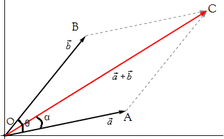
Parallelogram Law
"If two forces acting simultaneously on a particle is represented in magnitude and direction by two adjacent sides of a parallelogram, their resultant may be represented in magnitude and direction by the diagonal of the parallelogram which passes through the point of intersection."
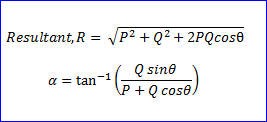
Question 10) Explain Force system.
Answer:
It is an external agency which produces or tends to produce, destroy or tends to destroy motion. OR
It is an external agent which changes or tends to change the state of motion of body.
It is a vector quantity.
Force is also known as rate of change of momentum.
As momentum = mass x velocity
But mass will never change, then
Force = mass x rate of change of velocity
= mass x Acceleration
F = P = ma
S.I. Unit: - Newton (N)
Kilo Newton (KN) = 103 N
Mega Newton (MN) = 106 N
Giga Newton (GN) = 103 N
Tera Newton (TN) = 1012 N
1 Kg Force:-
Force required producing unit gravitational acceleration on unit mass.
01 kg force = mass x Acceleration (gravity)
= 1 kg x 9.81 m / s2
= 9.81 kg.m / s2
1 kg.F = 9.81 Kg m / s2
1 kg.F = 9.81 N
I.e. 1 Kg = 9.81 N
Characteristics of Force:-
1. Magnitude: - The value of force i.e. 10N, 2KN, etc.
2. Direction:- Line of action & angle formed with fixed axis.
3. Nature of force or sense:-It means whether the force is push or pull.
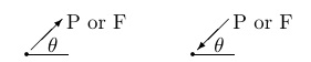
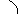
Pull type force Push type force
Push: - Force acting towards the point
Pull: - Force acting away from the point.
4. Point of application:-
The point at which or through which the force acts.
Effects of Force:-
Force may produce following effects on the body.
1. It may change the state of body.
i.e. if body is at rest, force may bring it in motion or if body is in motion, force may accelerate it or force may stop it or may retard it.
2. It may produce internal stress in the body.
3. It may produce deformation in non-rigid body.
4. It may produce rotational effect in body.
5. It may keep the body in stable state (Equilibrium).
Unit 1
Introduction to Mechanics
Question 1) Explain engineering mechanics.
Answer:
Mechanics is the physical science concerned with the behaviour of bodies that are acted upon by forces. Mechanics is a branch of the physical sciences concerned with the state of rest or motion of bodies that are subjected to the action of forces. The study of mechanics involves many more subject areas. However, initial study is usually split into two areas; statics and dynamics.
Statics is concerned with bodies that are either at rest or move with a constant speed in a fixed direction. Dynamics deals with the accelerated motion of bodies. Statics can therefore be considered as a special case of dynamics where the acceleration is zero. In engineering, since many objects are designed with the intention that they are at rest or their motion remains constant, statics deserves special treatment.
Question 2) Explain Idealisations of mechanics.
Answer:
In mechanics we look at real life situations and try to predict what will happen. The problem with real life is that it is often quite complicated. When studying problems in mechanics we often make idealisations of real life situations that simplify the problem. There are many commonly used idealisations that we will introduce in later sheets. Here follows a list of some common idealisations that are used in mechanics.
Particles are bodies which can be treated as a point mass in a given context. For example, when modelling the motion of the planets around the Sun, the planets and Sun can be treated as particles. Much of basic mechanics study is concerned with objects that can be treated as particles.
Connected particles arise in problems where two objects are attached in some way and both objects can be treated as particles. For example, two masses, connected by a string which passes over a pulley could be modelled as connected particles.
Rigid bodies can be considered as combinations of particles in which all the particles remain at a fixed distance from one another both before and after applying a force i.e. there is no bending or stretching. For example a brick can in most circumstances be thought of as a rigid body. Many real life objects can be considered to be rigid bodies to a good approximation.
Question 3) Explain Fundamental concept of mechanics.
Answer:
Certain concepts and definitions are basic to the study of mechanics and they should be understood at the outset. The basic concepts in mechanics are space, time, mass and force. These concepts cannot be truly defined. They should be accepted on the basis of our intuition and experience, and used as a mental frame of reference for our study of mechanics.
In Newtonian mechanics, space, time and mass are absolute quantities, which mean that they are independent of each other (this is not true in Relativistic Mechanics, where the time of an event depends upon its position and the mass of
a body varies with its velocity) and cannot be defined in terms of other quantities
Or in simpler terms. Force is a derived quantity.
Question 4) Explain ACTIONS AND EFFECTS OF FORCES?
Answer:
A force is defined as the action of a body on another body. A force is applied either through a direct contact or through a remote action. Forces applied through a remote action are gravitational, electrical, and magnetic forces. All other forces are applied through direct contacts.
Force acting on a body produces effects that can be divided into two types, namely external effect and internal effect.
As an illustration, consider the structure portrayed Assume that the structure is of negligible mass. The applied force F acting on the structure causes the reactive forces R1 and R2 which are applied by the support surfaces onto the structure so as to balance F. The reactions R1 and R2 are effects external to the body which are caused by F. Hence, external forces acting on a body are of two types, namely applied external forces (also called active forces) and reactive forces.
Besides causing the reactions R1 and R2, the applied force F also causes effects internal to the members of the structure. These effects are in the forms of stresses and strains that appear in the material of the structure. The effects exist to balance the respective external actions and effects.
In the study of mechanics, only the external effects of a force are considered. The internal effects are studied in disciplines of study specific to them, for example Mechanics of Materials (also known as Strength of Materials).
Question 5) Explain Characteristics of force.
Answer:
- Force can introduce motion in a body.
- Force can change direction of a moving body.
- Force can change size of an object.
- Force is a vector quantity.
- Force can stop a moving body.
- Force has a unit of Newton (N) in M.K.S system and dyne in C.G.S system.
- They are of two types: contact and non-contact forces.
Force system is a collection of forces acting at specified locations.
Different types of force system:
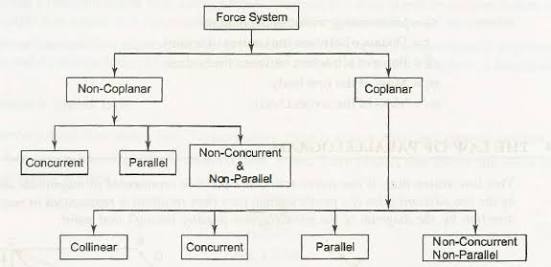
(i) COPLANAR FORCES:
Forces acting on only one plane are known as coplanar force system.
Or, we can say that if the effect of forces is only in one plane of object then the force system is known as coplanar force.
Ii) CONCURRENT FORCES:
A concurrent coplanar force system is a system of two or more forces whose lines of action ALL intersect at a common point.
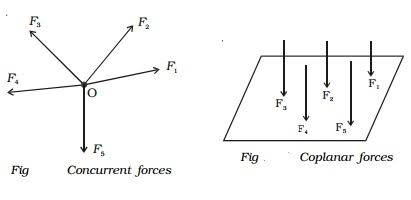
Iii) LIKE FORCES
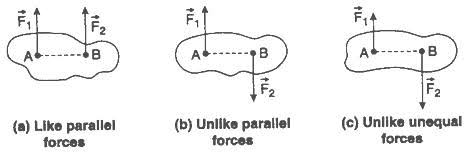
Parallel coplanar force system consists of two or more forces whose lines of action are all parallel to one another.
Iv) UNLIKE FORCES:
If the parallel forces are such that their directions are opposite to each other, then they are termed as "UNLIKE FORCE".
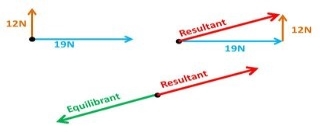
Question 6) Explain equilibrant force.
Answer:
Equilibrant force is equal in magnitude but opposite in direction to the resultant force of all the forces acting on a body.
- Equilibrant force= - resultant force
- R=√[(a^2+b^2+2abcos@)]
- R=√[(60)^2+(40)^2)+2*60*40*cos(90°)]
- R=√5200
- R=72.112
If two forces are equal in opposite directions, each force is the equilibrant of the other. The equilibrant force is labelled as FQ is equal in magnitude but opposite in direction to the resultant vector. (FQ = -FR)
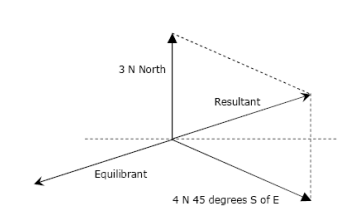
The equilibrant force is the single force that if applied at the same point (equal in magnitude and opposite on direction) that produces equilibrium.
Question 7) Explain Resultant force.
Answer:
Resultant force
When an object is subject to several forces, the resultant force is the force that alone produces the same acceleration as all those forces.
For example, if 4 forces act on a block and cause it to accelerate 1 m/s2 south, then the resultant force is the force that, if applied alone to the block, will also make it accelerate 1 m/s2 south.
The reason why the resultant force is useful is that it allows us to think about several forces as though they were a single force. This means that to determine the effect that several forces have on an object, we only need to determine the effect that a single force has.
If we know the mass m of an object and the acceleration a produced by the forces that act on it, we can find the resultant force using Newton's Second Law. Indeed, according to Newton's Second Law, the force F that alone produces the acceleration a on an object of mass m is:
F = ma
This force F is our resultant force. So, we can write:
R = ma
Which indicates that the resultant force R has the same direction as a, and has magnitude equal to the product ma.
For example, if a box of 1.5 kg is subject to 5 forces which make it accelerate 2.0 m/s2 north-west, then the resultant force is directed north-west and has the magnitude equal to 1.5 kg × 2.0 m/s2 = 3.0 N.
Often, however, we know the forces that act on an object and we need to find the resultant force. Experiments show that when an object is subject to several forces, F1, F2 the resultant force R is the vector sum of those forces:
R = F1 + F2 +…
Notice that this is not a mere sum of the magnitudes of the forces, but the sum of the forces taken as vectors, which is more involved because vectors have both a magnitude and a direction that we need to consider when doing the sum.
According to the above equation, if an object is subject to no forces, then the resultant force is zero, and if an object is subject to only one force, then the resultant force is equal to that force. These two cases are pretty simple, but what about an object subject to two or more forces.
To explain this clearly, we will now go through all the cases that can happen, from simple ones in which all the forces are parallel, to more complex ones in which the forces are not parallel, and show how to find the resultant force in each of them with the help of examples.
Question 8) Explain Resolution and composition of forces.
Answer:
Resolution of a Force
The process of substituting a force by its components so that the net effect on the body remains the same is known as resolution of a force.
- For each force, there exist an infinite number of possible sets of components.
Suppose a force is to be resolved into two components. Then:
- When one of the components is known, the second component can be obtained by applying the triangle rule.
- When the line of action of each component is known, the magnitude and the sense of the components are obtained by parallelogram law.
Question 9) Explain Principle of Resolution.
Answer:
The algebraic sum of the resolved parts of a number of forces in the given direction is equal to the resolved part of their resultant in the same direction.
Composition of Forces
The process of finding out the resultant force of a number of given forces is called the composition/compounding of forces.
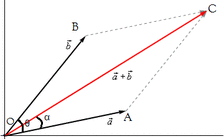
Parallelogram Law
"If two forces acting simultaneously on a particle is represented in magnitude and direction by two adjacent sides of a parallelogram, their resultant may be represented in magnitude and direction by the diagonal of the parallelogram which passes through the point of intersection."
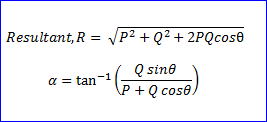
Question 10) Explain Force system.
Answer:
It is an external agency which produces or tends to produce, destroy or tends to destroy motion. OR
It is an external agent which changes or tends to change the state of motion of body.
It is a vector quantity.
Force is also known as rate of change of momentum.
As momentum = mass x velocity
But mass will never change, then
Force = mass x rate of change of velocity
= mass x Acceleration
F = P = ma
S.I. Unit: - Newton (N)
Kilo Newton (KN) = 103 N
Mega Newton (MN) = 106 N
Giga Newton (GN) = 103 N
Tera Newton (TN) = 1012 N
1 Kg Force:-
Force required producing unit gravitational acceleration on unit mass.
01 kg force = mass x Acceleration (gravity)
= 1 kg x 9.81 m / s2
= 9.81 kg.m / s2
1 kg.F = 9.81 Kg m / s2
1 kg.F = 9.81 N
I.e. 1 Kg = 9.81 N
Characteristics of Force:-
1. Magnitude: - The value of force i.e. 10N, 2KN, etc.
2. Direction:- Line of action & angle formed with fixed axis.
3. Nature of force or sense:-It means whether the force is push or pull.
Pull type force Push type force
Push: - Force acting towards the point
Pull: - Force acting away from the point.
4. Point of application:-
The point at which or through which the force acts.
Effects of Force:-
Force may produce following effects on the body.
1. It may change the state of body.
i.e. if body is at rest, force may bring it in motion or if body is in motion, force may accelerate it or force may stop it or may retard it.
2. It may produce internal stress in the body.
3. It may produce deformation in non-rigid body.
4. It may produce rotational effect in body.
5. It may keep the body in stable state (Equilibrium).