Unit 3
Unit 3
Principle of virtual work
Question 1) John throws a ball and it moves along the horizontal direction. If it travels a distance of 30 m in 2s. Calculate its acceleration.
Solution:
Known: u (Initial velocity) = 0,
s (Distance travelled) = 30 m,
t (Time taken) = 2 s
Distance travelled is given by
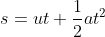
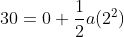


Question 2) If v2=u2+2as and find the value of ‘v‘, if u=0, a=3, s=150 is given.
Solution:
Known: u (Initial velocity) = 0,
s (Distance travelled) = 150 m,
a (acceleration) = 3 m/s2
v2=u2+2as
v2 = 0 + (2×3×150)
v2 = (2×3×150)
v2 = 900
Final velocity v = ±30 m/s
Question 3) Explain Stable Equilibrium?
Answer:
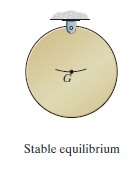
A system is said to be stable if a system has a tendency to return to its original position when a small displacement is given to the system. The potential energy of the system in this case is atits minimum.A simple example is shown in Fig. Below.When the disk isgiven a small displacement, its center of gravity G will always move(rotate) back to its equilibrium position, which is at the lowest point of itspath.This is where the potential energy of the disk is at its minimum.
The graph represents stable equilibrium for one degree of freedom system.
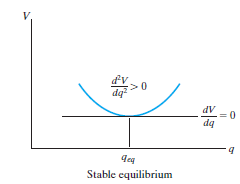
Question 4) Explain Neutral Equilibrium?
Answer:
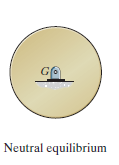
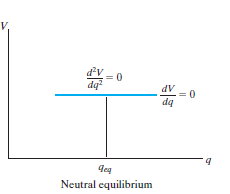
A system is said to be in neutral equilibriumif the system still remains in equilibrium when the system is given asmall displacement away from its original position. In this case, thepotential energy of the system is constant. Neutral equilibrium is shownin Fig. Below, where a disk is pinned at G. Each time the disk is rotated,a new equilibrium position is established and the potential energyremains unchanged.
Question 5) Explain Unstable Equilibrium?
Answer:
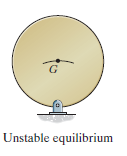
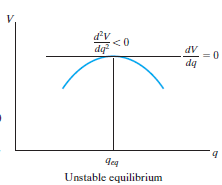
A system is said to be unstable if it has atendency to be displaced further away from its original equilibriumposition when it is given a small displacement. The potential energy ofthe system in this case is a maximum. An unstable equilibrium positionof the disk is shown in Fig. Below. Here the disk will rotate away from itsequilibrium position when its center of gravity is slightly displaced. Atthis highest point, its potential energy is at a maximum.
A system is said to be in stable equilibrium if, when displaced from equilibrium, it experiences a net force or torque in a direction opposite to the direction of the displacement. For example, a marble at the bottom of a bowl will experience a restoring force when displaced from its equilibrium position. This force moves it back toward the equilibrium position. Most systems are in stable equilibrium, especially for small displacements. For another example of stable equilibrium, see the pencil in Figure 2.
Question 6) what is kinematics?
Answer:
Kinematics, the part of physics we have studied up to this point, deals with describing motion. We have looked at position, velocity and acceleration as the three basic properties of a particle in motion. In Dynamics, we look at the causes of the motion that we have already studied. In studying these causes, which we shall call forces, we can get a more complete picture of a given physical situation. Starting with a given set of forces, through dynamics we are able to describe all resulting motion. Dynamics is thus the basis for the rest of the study of classical mechanics, and is applied in every branch of physics.
The study of Dynamics begins with an introduction of the concepts of force and mass, then goes on to introduce the basic laws of Dynamics, Newton's Three Laws. From here, we will look at how Newton's Laws are applied to a variety of forces, including tension, friction, and gravity. We will also examine the Dynamics of uniform circular motion.
Question 7) Define rectilinear motion.
Answer:
Rectilinear motion
Motion is one of the most common phenomena we come across in our daily lives. For example, a moving car, a kid running on the road or a fly moving in the air are all said to be in motion. So, in general terms, a body is said to be in motion if it changes its position with respect to a reference point and time. Depending upon the path taken by the particle the motion can be of different types like projectile motion, rectilinear motion, rotational motion, etc. For now, we will only focus on the rectilinear motion which is also known as linear motion.
When we require only one co-ordinate axis along with time to describe the motion of a particle it is said to be in linear motion or rectilinear motion. Some examples of linear motion are a parade of soldiers, a train moving along a straight line, and many more.
Question 8) Difference between Periodic, Oscillation and Simple Harmonic Motion.
Answer:
Periodic Motion
- A motion repeats itself after an equal interval of time. For example, uniform circular motion.
- There is no equilibrium position.
- There is no restoring force.
- There is no stable equilibrium position.
Oscillation Motion
- To and fro motion of a particle about a mean position is called an oscillatory motion in which a particle moves on either side of equilibrium (or) mean position is an oscillatory motion.
- It is a kind of periodic motion bounded between two extreme points. For example, Oscillation of Simple Pendulum, Spring-Mass System.
- The object will keep on moving between two extreme points about a fixed point is called mean position (or) equilibrium position along any path. (the path is not a constraint).
- There will be a restoring force directed towards equilibrium position (or) mean position.
- In an oscillatory motion, the net force on the particle is zero at the mean position.
- The mean position is a stable equilibrium position.
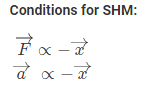
Simple Harmonic Motion or SHM
- It is a special case of oscillation along with straight line between the two extreme points (the path of SHM is a constraint).
- Path of the object needs to be a straight line.
- There will be a restoring force directed towards equilibrium position (or) mean position.
- Mean position in Simple harmonic motion is a stable equilibrium.
Question 9) what are the Types of Simple Harmonic Motion?
Answer:
SHM or Simple Harmonic Motion can be classified into two types,
- Linear SHM
- Angular SHM
Linear Simple Harmonic Motion
When a particle moves to and fro about a fixed point (called equilibrium position) along with a straight line then its motion is called linear Simple Harmonic Motion.
For Example: spring-mass system
Conditions for Linear SHM:
The restoring force or acceleration acting on the particle should always be proportional to the displacement of the particle and directed towards the equilibrium position.

Angular Simple Harmonic Motion
When a system oscillates angular long with respect to a fixed axis then its motion is called angular simple harmonic motion.
Conditions to Execute Angular SHM:
The restoring torque (or) Angular acceleration acting on the particle should always be proportional to the angular displacement of the particle and directed towards the equilibrium position.
Τα–θ or αθ– Τ
Where,
- Τ – Torque
- α angular acceleration
- θ– angular displacement
Mean Position
The point at which net force acting on the particle is zero.
From the mean position, the force acting on the particle is,

The force acting on the particle is negative of the displacement. So this point of equilibrium will be a stable equilibrium.
Question 10) How do we measure energy and work?
Answer:
The standard unit used to measure energy and work done in physics is the joule, which has the symbol J. In mechanics, 1 joule is the energy transferred when a force of 1 Newton is applied to an object and moves it through a distance of 1 meter.
Another unit of energy you may have come across is the Calorie. The amount of energy in an item of food is often written in Calories on the back of the packet. A typical 60 gram chocolate bar for example contains about 280 Calories of energy. One Calorie is the amount of energy required to raise 1 kg of water by 1∘degrees Celsius. This is equal to 4184 joules per Calorie, so one chocolate bar has 1.17 million joules or 1.17 MJ of stored energy.
Unit 3
Principle of virtual work
Question 1) John throws a ball and it moves along the horizontal direction. If it travels a distance of 30 m in 2s. Calculate its acceleration.
Solution:
Known: u (Initial velocity) = 0,
s (Distance travelled) = 30 m,
t (Time taken) = 2 s
Distance travelled is given by

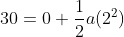

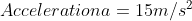
Question 2) If v2=u2+2as and find the value of ‘v‘, if u=0, a=3, s=150 is given.
Solution:
Known: u (Initial velocity) = 0,
s (Distance travelled) = 150 m,
a (acceleration) = 3 m/s2
v2=u2+2as
v2 = 0 + (2×3×150)
v2 = (2×3×150)
v2 = 900
Final velocity v = ±30 m/s
Question 3) Explain Stable Equilibrium?
Answer:
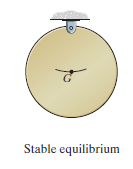
A system is said to be stable if a system has a tendency to return to its original position when a small displacement is given to the system. The potential energy of the system in this case is atits minimum.A simple example is shown in Fig. Below.When the disk isgiven a small displacement, its center of gravity G will always move(rotate) back to its equilibrium position, which is at the lowest point of itspath.This is where the potential energy of the disk is at its minimum.
The graph represents stable equilibrium for one degree of freedom system.

Question 4) Explain Neutral Equilibrium?
Answer:
A system is said to be in neutral equilibriumif the system still remains in equilibrium when the system is given asmall displacement away from its original position. In this case, thepotential energy of the system is constant. Neutral equilibrium is shownin Fig. Below, where a disk is pinned at G. Each time the disk is rotated,a new equilibrium position is established and the potential energyremains unchanged.


Question 5) Explain Unstable Equilibrium?
Answer:
A system is said to be unstable if it has atendency to be displaced further away from its original equilibriumposition when it is given a small displacement. The potential energy ofthe system in this case is a maximum. An unstable equilibrium positionof the disk is shown in Fig. Below. Here the disk will rotate away from itsequilibrium position when its center of gravity is slightly displaced. Atthis highest point, its potential energy is at a maximum.
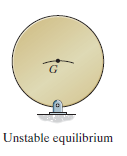
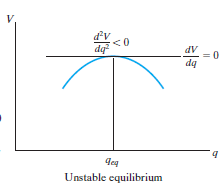
A system is said to be in stable equilibrium if, when displaced from equilibrium, it experiences a net force or torque in a direction opposite to the direction of the displacement. For example, a marble at the bottom of a bowl will experience a restoring force when displaced from its equilibrium position. This force moves it back toward the equilibrium position. Most systems are in stable equilibrium, especially for small displacements. For another example of stable equilibrium, see the pencil in Figure 2.
Question 6) what is kinematics?
Answer:
Kinematics, the part of physics we have studied up to this point, deals with describing motion. We have looked at position, velocity and acceleration as the three basic properties of a particle in motion. In Dynamics, we look at the causes of the motion that we have already studied. In studying these causes, which we shall call forces, we can get a more complete picture of a given physical situation. Starting with a given set of forces, through dynamics we are able to describe all resulting motion. Dynamics is thus the basis for the rest of the study of classical mechanics, and is applied in every branch of physics.
The study of Dynamics begins with an introduction of the concepts of force and mass, then goes on to introduce the basic laws of Dynamics, Newton's Three Laws. From here, we will look at how Newton's Laws are applied to a variety of forces, including tension, friction, and gravity. We will also examine the Dynamics of uniform circular motion.
Question 7) Define rectilinear motion.
Answer:
Rectilinear motion
Motion is one of the most common phenomena we come across in our daily lives. For example, a moving car, a kid running on the road or a fly moving in the air are all said to be in motion. So, in general terms, a body is said to be in motion if it changes its position with respect to a reference point and time. Depending upon the path taken by the particle the motion can be of different types like projectile motion, rectilinear motion, rotational motion, etc. For now, we will only focus on the rectilinear motion which is also known as linear motion.
When we require only one co-ordinate axis along with time to describe the motion of a particle it is said to be in linear motion or rectilinear motion. Some examples of linear motion are a parade of soldiers, a train moving along a straight line, and many more.
Question 8) Difference between Periodic, Oscillation and Simple Harmonic Motion.
Answer:
Periodic Motion
- A motion repeats itself after an equal interval of time. For example, uniform circular motion.
- There is no equilibrium position.
- There is no restoring force.
- There is no stable equilibrium position.
Oscillation Motion
- To and fro motion of a particle about a mean position is called an oscillatory motion in which a particle moves on either side of equilibrium (or) mean position is an oscillatory motion.
- It is a kind of periodic motion bounded between two extreme points. For example, Oscillation of Simple Pendulum, Spring-Mass System.
- The object will keep on moving between two extreme points about a fixed point is called mean position (or) equilibrium position along any path. (the path is not a constraint).
- There will be a restoring force directed towards equilibrium position (or) mean position.
- In an oscillatory motion, the net force on the particle is zero at the mean position.
- The mean position is a stable equilibrium position.
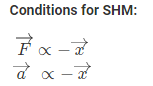
Simple Harmonic Motion or SHM
- It is a special case of oscillation along with straight line between the two extreme points (the path of SHM is a constraint).
- Path of the object needs to be a straight line.
- There will be a restoring force directed towards equilibrium position (or) mean position.
- Mean position in Simple harmonic motion is a stable equilibrium.
Question 9) what are the Types of Simple Harmonic Motion?
Answer:
SHM or Simple Harmonic Motion can be classified into two types,
- Linear SHM
- Angular SHM
Linear Simple Harmonic Motion
When a particle moves to and fro about a fixed point (called equilibrium position) along with a straight line then its motion is called linear Simple Harmonic Motion.
For Example: spring-mass system
Conditions for Linear SHM:
The restoring force or acceleration acting on the particle should always be proportional to the displacement of the particle and directed towards the equilibrium position.

Angular Simple Harmonic Motion
When a system oscillates angular long with respect to a fixed axis then its motion is called angular simple harmonic motion.
Conditions to Execute Angular SHM:
The restoring torque (or) Angular acceleration acting on the particle should always be proportional to the angular displacement of the particle and directed towards the equilibrium position.
Τα–θ or αθ– Τ
Where,
- Τ – Torque
- α angular acceleration
- θ– angular displacement
Mean Position
The point at which net force acting on the particle is zero.
From the mean position, the force acting on the particle is,

The force acting on the particle is negative of the displacement. So this point of equilibrium will be a stable equilibrium.
Question 10) How do we measure energy and work?
Answer:
The standard unit used to measure energy and work done in physics is the joule, which has the symbol J. In mechanics, 1 joule is the energy transferred when a force of 1 Newton is applied to an object and moves it through a distance of 1 meter.
Another unit of energy you may have come across is the Calorie. The amount of energy in an item of food is often written in Calories on the back of the packet. A typical 60 gram chocolate bar for example contains about 280 Calories of energy. One Calorie is the amount of energy required to raise 1 kg of water by 1∘degrees Celsius. This is equal to 4184 joules per Calorie, so one chocolate bar has 1.17 million joules or 1.17 MJ of stored energy.