Unit-4
Electrical Machines
Question Bank
Q1) A 4 pole lap wound dc shunt generator has a useful flux per pole of 0.05 Wb. The armature winding consists of 200 turns each of 0.06 u ohm resistance. Calculate the terminal voltage when running at 900 rpm with armature current of 50 A.
Soln. Terminal voltage V =Ea – Ia Ra
Ia Ra = 50×Ra.
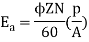
Z = 200×2=400 (each turn has two sides).
N = 900 rpm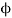 = 0.05 WbP = A = 4
= 0.05 WbP = A = 4
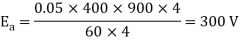
Total resistance of 200 turns = 200 × 0.004 = 0.8 ohm
As there are 4 parallel paths, so resistance of each path = 0.8/4 = 0.2 ohm
There are 4 resistances in parallel of each of 0.2 ohm
Ra = 0.2/4 = 0.05 ohm
Ia Ra = 50×0.05 = 25 V
V = Ea – Ia Ra = 300 – 25 = 275 V
Q2) A 220 V 4 pole wave wound dc series motor has 780 conductor on its armature. It has armature and series field resistance of 0.75 ohm. The motor takes a current of 30A. Find the speed and gross torque developed if flux/pole is 20 mWb?
Soln. Back emf, 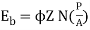
Eb = V – IaRa = 220 – (30×0.75) = 197.5 V
197.5 = 20 × 10-3 ×780×N×0.75
N = 16.88 ≈ 17
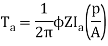
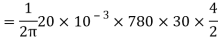
Ta = 158.97 Nm.
Q3) A 2500/200 V transformer draws a no-load primary current of 0.5 A and absorbs 400 W. Find magnetising and loss currents.
Sol: Iron-loss current = No load input(W) / Primary voltage
= 400/2500 = 0.16 A
I20 = I2w + I2µ
Iµ = √I20 – I2w
= √ (0.5)2 – (0.16)2
Iµ = 0.473 A
Q4) A 1-φ transformer has 1000 turns on primary and 200 on secondary. The no load current is 4 amp at p.f of 0.2 lagging. Find primary current and pf when secondary current is 280 A at pf of 0.6 lagging.
Sol : cos-1 0.6 = 53.130 (sin φ = 0.8)
I2 = 280/-53.130A
Φ = cos-1 0.2 = 78.50
Sin φ = 0.98
I1 = I0 + I’2
I’2 = (I2/K) ( -53.130
K = N1/N2 = 1000/200 = 5
I’2 = 280/5 (-53.130
I’2 = 56(-53.130
I1 = I0 + I’2
= 4(0.20 – j0.98) + 56(0.6 – j0.8)
= 0.80 – j3.92 + 33.6 – j44.8
I1 = 34.4 – j48.72
I1 = 59.64 ( -54.770
I lags supply voltage by 54.770
Q5) When operated at 120 V in the primary of an iron core transformer, the current in the primary is 5 amps. Find the current in the secondary if the voltage is stepped up to 400 V.
Sol: VP/VS = IS/IP
120/400 = IS/5
IS = 1.5A
Q6) A transformer with 400 turns on the primary and 60 turns on the secondary draws Solution: 0.5 amps from a 120 V line. Find Is.
Sol: NP/NS = IS/IP
400/60 = IS/0.5
IS = 3.34A
Q7) The core of a 110 KVA, 10,000/500v, 50 Hz, 1-Φ core type transformer has a cross section of 18 cm x 18 cm. Find the number of HV and LV turns per phase and the emf per turn if the maximum core density does not exceed 1.3 tesla. Assume a stacking factor pf 0.9.
Sol: Bm= 1.3T
Area = (0.18 x 0.18) = 0.032m2
Emf induced in primary
E1 = 4.44 fN1BmA
10000=4.44 x 50 x N1 x 1.3 x 0.032
N1=1082.8
Emf induced in secondary
E2 = 4.44 fN2BmA
500= 4.44 x 50 x N2 x 1.3 x 0.032
N2= 54.14
i) The number of turns is N1=1082.8 and N2= 54.14
Ii) Emf per turn = E1/E2 = N1/N2 = K
=10000/1082=9.24V or 500/54.14=9.23V
Q8) A 1-Φ transformer has 400 turns in primary and 110 turns in the secondary. The cross-sectional area of the secondary. The cross-sectional area of the core is 80cm2. If the primary winding is connected to the 50 Hz supply at 500V. Calculate peak flux density in core.
Sol: As we know Emf induced in primary
E1 = 4.44 fN1BmA
500 = 4.44 x 50 x 400 x Bm x (80x10‑4)
Bm=0.704Wb/m2
Q.9) A single phase transformer has 400 turns in primary and 1000 turns in secondary. The cross-sectional area is 80 cm2. If primary is connected to 50hz at 500V. Voltage induced in secondary?
Sol: As we know Emf induced in primary
E1 = 4.44 fN1BmA
500= 4.44x50x1000xBmx(80x10-4)
Bm= 0.28Wb/m2
The voltage induced in secondary is given as
E1/E2 = N1/N2 = K
E2=1000x500/400=1250V
Q10) A rotor of 6-pole 50Hz IM is rotated by some means at 1000 rpm. Find i) Rotor voltage. Ii) rotor frequency iii) rotor slip.
Sol: N=1000rpm
F=50Hz
The synchronous speed Ns=120f/P=120x50/6=1000rpm
i) Rotor voltage Er=sE
S=Ns-N/Ns x100 = {[1000-1000]/1000} x 100 = 0
Since, s=0 Er=0
Ii) Rotor Frequency fr=sfs
Since, s=0
fr=0
Iii) Rotor slip s=0
Q11) The power input to a rotor of a 400V, 50hz,6-pole, 3-phaseinduction motor is 15kW. The slip is 4%. Calculate i) frequency of rotor current. i)rotor speed. Iii)rotor cu loss iv) rotor resistance/phase if rotor current is 50A?
Sol: i) frequency of rotor current=sf=0.04 x 50=2Hz
Ii) Rotor speed N=(1-s) Ns=(1-0.04) x 1000=960rpm
Ns=120f/P=120 x 50/6=1000rpm
Iii) rotor cu loss=s x rotor input=0.04 x 15=0.6kW
Iv)rotor cu loss/phase=0.6 x 1000/3=200W
602R2=200
R2=0.055Ω
Q12) A 230V shunt motor on no load runs at 1000rpm and takes 5A. Armature and shun field resistances are 0.3 and 250ohm. Calculate the speed when load taking a current of 50A. The armature reaction weakens the field by 4%.
Sol: Ish= 230/250=0.92A
Ia1=5-0.92=4.08A
Ia2=50-0.92=49.08A
Eb1=230-(4.08 x 0.3) =228.776V
Eb2=230-(49.08 x 0.3) =215.276V
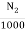 =
=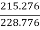 =940.99rpm
=940.99rpm
Q13) A 250V shunt motor has an armature resistance of 0.5 ohm and takes an armature current of 35A on a certain load. What amount the main flux will reduce to raise the speed by 50% if torque is constant.
Sol: As we already know
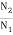 =
= 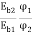
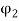 Ia2 α
Ia2 α 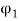 Ia1
Ia1
Ia2 = Ia1 x 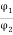
Eb1= 250- (35 x 0.5) = 232.5V
Eb2= 250- (35k x 0.5)
Let 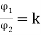
As we need to raise the speed by 50% then  =
= 
Substituting in above equation we get
 =
=  x k
x k
35k2-500k + 697.5=0
K = 1.56
The other value of k does not hold for this question.
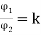 =1.56
=1.56
So, the percentage reduction in the main flux will be given as

 = 35.89%
= 35.89%