Unit 4

Unit 4

Curvilinear translation

Question 1) Explain the Types of Rectilinear Motion?

Answer:

There are three types of rectilinear motion and they are:

• Uniform rectilinear motion: When an object travels at a constant speed with zero acceleration it is known as uniform rectilinear motion.
• Uniformly accelerated rectilinear motion: When an object travels with constant acceleration it is known as uniformly accelerated rectilinear motion.
• Rectilinear movement with non-uniform acceleration: When an object travels at an irregular speed and acceleration it is known as a rectilinear movement with non-uniform acceleration.

Question 2) what is the difference between linear and rectilinear motion?

Answer:

Question 3) Give examples of curvilinear motion?

Answer:

The particles move from one point to another in a curved path. In the case of curvilinear motion, two types of force come into the picture, i.e., the centrifugal force and centripetal force. Centripetal force is the force acting towards the centre of the circular path. Whereas, the centrifugal force acts in a direction pointing away from the centre of the circle.

Examples

• Throwing the ball into the air in a curved way,
• Motion of a jet in curved path
• Turning a car
• Planets revolving around the orbit

Question 4) Explain the difference between rectilinear and curvilinear translatory motion, for your better understanding.

Answer:

Question 5) what is Translatory Motion?

Answer:

A type of motion in which all parts of the body move the same distance in a given time is known as the translatory motion. Translatory motion can be of two types: rectilinear and curvilinear.

If a body moves as a whole such that every part of the body moves through the same distance in a given time, then the body is said to be in translatory motion.

Translatory Motion Examples

Let us understand translational motion with the help of examples.

• Let’s imagine a rectangular block placed on the slanting edge of a right-angled triangle. If the block is assumed to slide down this edge without any side movement, every point in the rectangular block experiences the same displacement, and more importantly, the distance between the points is also maintained. In pure translational motion, every point in the body experiences the same velocity be it at any instant of time. Both the points, P1 and P2 undergo the exact same motions.

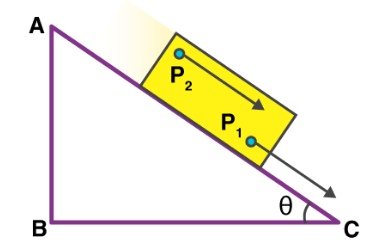
Question 6)What is the difference between linear and rectilinear motion?

Answer 6)

Question 7)What is Rotational Motion?

Answer 7)

Now let us imagine a circular block going down the edge of the right-angled triangle. Examining the location and orientation of different points on the cylindrical block will tell us something new. The points on the cylindrical body experience something much different from the rectangular block.

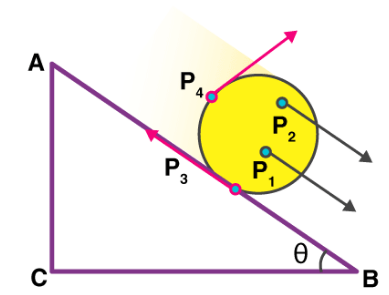
A circular block rolling down the slanting edge of a right-angled triangle experiences different magnitude of velocity in different directions.

As shown by the arrows in the diagram representing the velocity, each point experiences a different magnitude of velocity in a different direction. Here the points are arranged with respect to an axis of rotation. Rotation is what you achieve when you constrain a body and fix it along a straight line. This means that the body can only turn around the line, which is defined as rotational motion. A ceiling fan, a potter’s wheel, a vehicle’s wheel are all examples of rotational motion.

Say you go to a bowling alley, and throw the bowling ball towards the pins. If you notice closely, you will see that the ball is not just moving forwards i.e. performing translational motion but it is also spinning on itself because of which you can spin and curve the entry of the ball; this motion is categorized as rotational motion. The motion of a rigid body which is not fixed or pivoted is either a pure translational motion or a combination of translational and rotational motion. Rigid bodies are fixed/pivoted experience motion which is rotational.

Question 8) write examples Of Motion?

Answer:

Now let us understand motion clearly with the help of a few examples

.

• Our daily activities, like walking, running, closing the door, etc. involve motion. There is a change of position of the object involved in these activities.
• The flow of air in and out of our lungs is also an example of motion.
• The automobiles that carry passengers from the place of pick up to the destination possess motion. In this case, the position of passengers is changed from one place to another.

Question 9 )   the  position  of  a  particle  which  moves  along  a straight  line   is  defined  by  the  relation   S= t3  -  6t2  -  15  +  40  ,  where   S  is  in  meters  and  t  in  sec ;

Determine :-  a) time  at  which  velocity  will  be  zero .

                          b)   position  &  distance  travelled  by  particle  at  that  time  .

                          c)   Acceleration at that time.

                          d)  Distance travelled by particle from  t= 4 sec    to   t= 6sec

→            s = t3 -   6t2 -15t +40 

Differentiating w.r.t. Time‘t’

Ds/dt = 3t2 -12t - 15

∴ v = ds/dt =3t2 -12 t -15

Again differentiating w.r.t. Time‘t’

a= dv/dt = d2s/ dt2=  6t -12

a) time at  which  velocity  will be  zero 

For,  V =0

∴ v = 3t2 – 12t -15

∴ 0 =3t2 - 12t -15

Solving the equation 

[t = 5 sec]

B) t= 5 sec.  At this time Displacement will be,

∴Ss= t2-6t2 – 15t +40

∴Ss= (5)2 - (6 x 52) -(15 x  5 )+ 40

∴Ss= -60 m.

  At   t = 0 sec; displacement will be ,

S0 = t2-  6t2 – 15t + 40

∴ S0 = 40 m.

Question 10 )  the  motion  of  particle   is  defined   by   x  =  t3 -  6t2  -  36 t  -  40  in meterDetermine (1) when the velocity is zero. (2)  velocity  ,  acceleration  &  total  distance  travelled  when  x = 0 .

→given,

X=t3 - 6t2 -36t- 40

Differentiating w.r.t.t   we get

∴ v =dx /dt =3t2 – 12t - 36

Again differentiating w.r.t.  ‘t’

∴a= dv/dt =d2x/ d2t= 6t – 12

(1)  When the velocity is zero.

For, v= 0

V= 3t2-12t - 36

  0=  3t2 -  12t  - 36

Solving   above equation, we get 

[t = 6 sec.]

( 2)  velocity  ,  acceleration  &  total  distance  travelled  at x=0 .

For x = 0,       

x =t3 - 6t2 – 36t – 40

O =t3- 6t2 – 36t -40

Solving above equation, we get

T = 10sec.

∴velocity (for t =0)

V10 = 3t2 – 12 t – 36

= (3x102) - (12x10)-36

V10 = 144m/sec

∴acceleration (for t = 10)

A= 6t – 12

= (6x10)-12

A = 48m/sec2

Distance travelled   =|x10 – x6| + |x6 –x0|

∴x10 = 103 – ( 6 x 102)- ( 36 x 10 ) – 40

= 1000 – 600 – 360- 40  

X10 = 0m

∴x6 = 63 – (6x62) –(36x6) – 40

X6 = -256m   

∴x0  =  03 – 6 x 02   -36x 0 -40

X0 =-40 m

∴distance   travelled      = |0 – (-256)| +|-256 –(-40)|

=256 + 216

= 472m

Distance travelled = |ss- s0|

                                   =  |-60-40|

                                     =100m

(c) Acceleration at t = 5 sec 

A = 6t-12

= (6 x 5) -12

A = 18 m/s2 

(d) Distance   travelled   from 4 to 6 sec

As at t= 5sec, v =  0

Thus,

Distance   travelled     = distance  travelled from  4  to  5  sec  +    distance  travelled   from  5  to  6  sec.

=   |s5 – s4|+ |s6 – s5|

∴at   t = 6,       

s6 = 63 - (6 x 62) – (15 x 6) + 40

     =-50m

At    t   =4,         

s4 =   43  - (6 x 42) – (15 x 4 )  + 40

    =   -52m

Distance   travelled   = | -60 – (-52)|+|-50 – (-60)|

= 8+10

=   18m