Unit – 3
Development
Q1) Explain the Principle of Development.
A1)
Every line on the development should show the true length of the corresponding line on the surface which is developed.
Methods of Development
a) Parallel-line development. For developing prisms and cylinders.
b) Radial-line development. For developing pyramids and cones.
c) Triangulation development. For developing transition pieces.
d) Approximate development. For developing spheres.
Q2) Draw the development of the lateral surface of the part P of the pentagonal prism.
A2) Name the corners of the prism and the points at which the edges are cut.
(i) Draw the development assuming the prism to be whole [fig.(ii)]. It is made up of five equal rectangles.
(ii) Draw horizontal lines through points 1’, 2’ etc. to cut the lines for the corresponding edges in the development at points 1, 2 etc.
(iii)Draw lines joining these points and complete the development as shown.

Q3) Draw the development of the lateral surface of the truncated cone.
A3) Assuming the cone to be whole, let us draw its development.
(i) Draw the base-circle in the top view and divide it into twelve equal parts.
(ii) With any point O as centre and radius equal to o'1' or o'7', draw an arc of the circle [fig. 15-24(ii)]. The length of this arc should be equal to the circumference of the base circle. This can be determined in two ways.
(iii) Calculate the subtended angle θ by the formula,

Cut-off the arc so that it subtends the angle θ at the center and divide it into twelve equal parts.
(iv) Step-off with a bow-divider, twelve equal divisions on the arc, each equal to one of the divisions of the base-circle.
(This will give an approximate length of the circumference. Note that the base-circle should not be divided into less than twelve equal parts.)
(v) Join the division-points with 0, thus completing the development of the whole cone with twelve generators shown in it [fig. ,11(ii)].
(vi) The truncated portion of the cone may be deducted from this development by marking the positions of points at which generators are cut and then drawinga curve through them. For example, generators o'2' and o'12' in the front view are cut at points b' and b'1 which coincide with each other. The true length of o' b' may be obtained by drawing a line through b', parallel to the base and cutting o'7' at b". Then o'b" is the true length of o'b'.
(vii) Mark points B and 81 on generators 02 and 0-12 respectively, such that OB = 0B1 = o' b". Locate all points in the same way and draw a smooth curve through them. The figure enclosed this curve and the arc is the development of the truncated cone.
2. Draw the development of the lateral surface of the part P of the cone shown in fig.
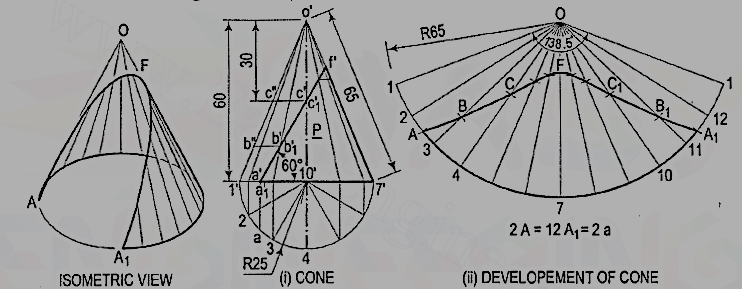
Draw the development as explained in problem [fig. (ii)]. For the points at which the base of the cone is cut, mark points A and A1 on the arcs2-3 and 11-12 respectively, such that A2 = A1 12 = a2. Draw the curve passing through the points A, B, C etc. The figure enclosed between this curve and the arcA-A1 is the required development.
3. Draw the projections of a cone resting on the ground on its base and show on them, the shortest path by which a point P, starting from a point on the circumference of the base and moving around the cone will return to the same point. Base of cone 61 mm diameter; axis 75 mm long.

(i) Draw the projections and the development of the surface of the cone showing all twelve generators (fig. 13). The development may be drawn attached to o'1 '.
(ii) Assume that P starts from the point 1 (i.e., point 1' in the front view). Draw a straight line 1 '1' on the development. This line shows the required shortest path. Let us take a point P4 at which the path cuts the generator o’4. Mark a point P"4 on o'1' such that o'P"4 = o'P4. This can be done by drawing an arc with o' as centre and radius equal to o'P 4 cutting o11'at P"4. Through P"4, draw a line parallel to the base cutting o'4' at P'4. Then p'4 is the position of the point p4 in the front view. Similarly, transfer all the points to the front view and draw the required curve through them. The curve at the back will coincide with the front curve.
(iii) Project these points to the top view on the respective generators. p'4 andp'10 cannot be projected directly. Hence, project p"4 to a point q on o1. With o as centre and radius equal to oq, draw an arc cutting o4 at p4 ando-10 at p10. Thus op4 = op10 = oq. A curve drawn through the points thus obtained will show the path in the top view.