UNIT – 3

TRANSMISSION OF HEAT AND THERMAL RADIATION

Q1) What is black body and black body radiation?  Also explain Emissive power and Absorptive power of a black body?

A1) A hot body emits thermal radiations which depend on composition and the temperature of the body. The ability of the body to radiate is closely related to its ability to absorb radiation.

 A Body which is capable of absorbing almost all the radiations incident on it is called a black body.

A perfectly black-body can absorb the entire radiations incident on it. Platinum black and Lamp black can absorb almost all the radiations incident on them.

Emissive power of a black body:

It is defined as the total energy radiated per second from the unit surface area of a black body maintained at certain temperature.

Absorptive power of a black body:

It is defined as the ratio of the total energy absorbed by the black body to the amount of radiant energy incident on it in a given time interval. The absorptive power of a perfectly black body is 1.

One of the major ideas of quantum physics is quantization, measuring quantities in discrete, not continuous units.

The problem of black-body radiation one of the earliest challenges to classical physics.

When you heat an object, it begins to glow. Even before the glow is visible, it’s radiating in the infrared spectrum. The reason it glows is that as you heat it, the electrons on the surface of the material are agitated thermally, and electrons being accelerated and decelerated radiate light.

Physics in the late 19th and early 20th centuries was concerned with the spectrum of light being emitted by black bodies. A black body is a piece of material that radiates corresponding to its temperature — but most ordinary objects you think of as black, such as charcoal, also absorb and reflect light from their surroundings.

Well, it was hard to come up with a physical black body after all, what material absorbs light 100% and doesn’t reflect anything? But the physicists were clever about this, and they came up with the hollow cavity with a hole in it.

As discussed the blackbody is an idealization, because no physical object absorbs 100% of incident radiation, we can construct a close realization of a blackbody in the form of a small hole in the wall of a sealed enclosure known as a cavity radiator, as shown in Figure.

Figure: Black Body

The inside walls of a cavity radiator are rough and blackened so that any radiation that enters through a tiny hole in the cavity wall becomes trapped inside the cavity. At thermodynamic equilibrium (at temperature T), the cavity walls absorb exactly as much radiation as they emit. Furthermore, inside the cavity, the radiation entering the hole is balanced by the radiation leaving it. The emission spectrum of a blackbody can be obtained by analyzing the light radiating from the hole. Electromagnetic waves emitted by a blackbody are called blackbody radiation.

Q2) Explain Spectral Distribution of energy in thermal radiation?

Or

Explain Black Body radiation spectrum?

A2) Spectral Distribution of energy in thermal radiation (Black Body radiation spectrum)

A good absorber of radiation is also a good emitter. Hence when a black body is heated it emits radiations. In practice a black body can be realized with the emission of Ultraviolet, Visible and infrared wavelengths on heating a body.

German physicists Lummer and Pringsheim studied the energy density as a function of wavelength for different temperatures of a black body using a spectrograph and a plot is made. This is called Black Body radiation spectrum.

Figure: Black Body radiation spectrum

You can see the spectrum of a black body (and attempts to model that spectrum) in the above figure, for different temperatures. one needs simply to analyse the spectral distribution of the radiation coming out of the hole. The radiation emitted by a blackbody when hot is called blackbody radiation.

The intensity I (λ, T) of blackbody radiation depends on the wavelength λ of the emitted radiation and on the temperature T of the blackbody.

The function I (λ, T) is the power intensity that is radiated per unit wavelength.

In other words, it is the power radiated per unit area of the hole in a cavity radiator per unit wavelength. According to this definition, I (λ, T) dλ is the power per unit area that is emitted in the wavelength interval from λ to λ+dλ.

 The intensity distribution among wavelengths of radiation emitted by cavities was studied experimentally at the end of the nineteenth century. Generally, radiation emitted by materials only approximately follows the blackbody radiation curve. However, spectra of common stars do follow the blackbody radiation curve very closely.

Experimental data about blackbody radiation was obtained for various objects. Following results obtained,

It turned out that the explanation of the blackbody spectrum was not so easy. The problem was that nobody was able to come up with a theoretical explanation for the spectrum of light generated by the black body. Everything classical physics could come up with went wrong.

Q3) What is Stefan’s law?

A3) The Stefan Boltzmann law describes the power radiated from a black body in terms of its temperature. Specifically, the Stefan Boltzmann law states that the total energy radiated per unit surface area of a black body across all wavelengths per unit time, is directly proportional to the fourth power of the black body's thermodynamic temperature T

E=eσT4
where σ= =5.670373×10−8 Wm−2K−4, Stefan Boltzmann constant.

E is the total energy radiated per unit surface area

T is the temperature of the object.

e is the emissivity (how good of a radiator/absorber the object is). The emissivity e is a correction for an approximate black body radiator, where e = 1 – R, is the fraction of the light reflected (R) by the black body. For a true black body R = 0 and e = 1 or total absorption. Which is less than or equal to 1; in the case of a blackbody e =1.

Q4) A body of emissivity (e = 0.75), the surface area of 300 cm2 and temperature 227 ºC are kept in a room at temperature 27 ºC. Using the Stephens Boltzmann law, calculate the initial value of net power emitted by the body.

A4) E = = eσ (T4 – T04)

P = eσA (T4 – T04)

P = (0.75) (5.67 × 10-8 W/m2 – k4) (300 × 10-4 m2) × [(500 K)4 – (300 K)4]

= 69.4 Watts.

Q5) Derive Stefan Boltzmann Law?

A5) The total power radiated per unit area over all wavelengths of a black body can be obtained by integrating Plank’s radiation formula. Thus, the radiated power per unit area as a function of wavelength is:

  ………. (1)

On simplifying Stefan Boltzmann equation, we get:

On integrating both the sides with respect to λ and applying the limits we get

The integrated power after separating the constants is:

     ………. (2)

This can be solved analytically by substituting:

x =          ………. (3)

Therefore, dx= d

d = d        ………. (4)

Moreover, h and c can also be written in terms of x as

h =          ………. (5)

c =          ………. (6)

Substituting the above equation (3), (4), (5) and (6) in equation (2)

= 2π (()2

= 2π (

= 2π (        ………. (7)

The above equation can be comparable to the standard form of integral:

=          ………. (8)

So, from equation (8) we can rewrite equation (7) as

= 2π (

= (        ………. (9)

On further simplifying we get,

 = σ         ………. (10)

Thus, we arrive at a mathematical form of Stephen Boltzmann law:

⇒ E = σ         ………. (11)

Where,

E =

Where σ= =5.670373×10−8 Wm−2K−4, Stefan Boltzmann constant.

So, this is the mathematical derivation of Stefan’s Law.

Q6) What is Wien’s law? Derive it?

A6) Wien’s law also called Wien’s displacement law. It is named after German physicist Wilhelm Wien, who received the Nobel Prize for Physics in 1911 for discovering the law.

This law gives relationship between the temperature of a blackbody and the wavelength at which it emits the most light.

Wien found that the radiative energy dW per wavelength interval dλ has a maximum at a certain wavelength λm and that the maximum shifts to shorter wavelengths as the temperature T is increased. He found that the product λmT is an absolute constant.

Mathematical representation of the law:

λmax =bT

Where, b is the Wien’s displacement constant =2897.8 µm K

T is the temperature in kelvins

Wien’s constant: b (Wien’s displacement constant)

Q7) A hot black body emits the energy at the rate of 16 J m-2 s-1 and its most intense radiation corresponds to 20,000 Å. When the temperature of this body is further increased and its most intense radiation corresponds to 10,000 Å, then find the value of energy radiated in Jm-2 s-1.

A7) Wein’s displacement law is, λm. T = b

i.e., T 1/ λm

so T1/T2 = λ2/λ1

so T1/T2 = 10,000/20,000 = 1/2

Here, λm   becomes half, the Temperature doubles.

Now from Stefan Boltzmann Law, e = sT4

e1/e2 = (T1/T2)4

⇒ e2 = (T2/T1)4. e1 = (2)4. 16

= 16.16 = 256 J m-2 s-1

Q8) Two spherical bodies A (radius 6 cm) and B (radius 18 cm) are at temperatures T1 and T2, respectively. The maximum intensity in the emission spectrum of A is at 500 nm and in that of B is at 1500 nm. Considering them to be black bodies, what will be the ratio of the rate of total energy radiated by A to that of B?

A8) Stefan-Boltzmann law gives the energy radiated per unit time by a spherical black body of area A=4πr2 and temperature T

E=σAT4=4πσr2T4.

The Wien's displacement law relates temperature of the black body to the wavelength at maximum intensity by λmT=b.

Eliminate T from above equations to get, E=4πσb4(r2/λ4), which gives,

=( ( =( ( =   9.

Q9) Discuss various mode of propagation of heat?

A9) Heat is defined as the form of energy that is transferred across a boundary by virtue of a temperature difference. The temperature difference is the 'potential' or 'force' and heat transfer i.e., the ''flux'.

The direction of heat transfer is taken from the high temperature system to the low temperature system. Heat flow into a system is taken to be positive, and heat flow out of a system is taken as negative. The symbol Q is used for heat transfer, i.e., the quantity of heat transferred within a certain time.

Heat is a form of energy in transit (like work transfer). It is a boundary phenomenon, since it occurs only at the boundary of a system, Energy transfer

by virtue of temperature difference only is called heat transfer. All other energy interactions may be termed as work transfer.

There are three modes in which heat may be transferred 

(a) Conduction

(b) Convection and

(c) Radiation

(a) Conduction

Conduction refers to the transfer of heat between two bodies or two pans of the same body through molecules which are more or less stationary. In liquids and gases conduction results from the transport of energy by molecular motion near the wall and in solids it takes place by a combination of lattice vibration and electron transport. In general, good electrical conductors are also good thermal conductors.

(b) Convection

Convection heat transfer occurs because of the motion of a fluid past a heated surface-the faster the motion, the greater the heat transfer. The convection heat transfer is usually assumed to be proportional to the surface area in contact with the fluid and the difference in temperature of the surface and fluid. Thus

Q =hA (TF-TI)

where h is called the convection heat transfer coefficient, which is a strong function of both fluid properties and fluid velocity (W/m2K).

(c) Radiation

Radiation heat transfer is the result of electromagnetic radiation emitted by a surface because of the temperature of the surface. This differs from other forms of electromagnetic radiation such as radio, television, X-rays and r-rays which are not related to temperature.

The transfer of heat between two bodies in direct contact is called conduction.

Heat may be transferred between two bodies separated by empty space or gases by the mechanism of radiation through electromagnetic waves. A third method of heat transfer is convection which refers to the transfer of heat between

a wall, and a fluid system in motion.

Q10) Define Thermal conductivity?

A10) Thermal conductivity K is defined as the amount of heat flowing per unit time through the material having unit area of cross-section per unit temperature gradient.

Q =K(dT/dx)

Q11) Derive Wien’s law?

A11) Physical constant defining the relationship between the thermodynamic temperature of the black body and the wavelength is known as Wien’s constant. It is a product of temperature and wavelength of the black body which grows shorter as the wavelength reaches a maximum with temperature.

The spectral distribution as a function of temperature is now to be examined more closely. It turns out that the maximum of the curve shifts with increasing temperature to ever shorter wavelengths. The dependence of this wavelength λmax. on the temperature is given by the following equation. This equation is also known as Wien’s displacement law.

λmax. = 2897.8 µm K / T   Wien’s displacement law

The Wien’s displacement law can be obtained by determining the maxima of Planck’s law. For this purpose, the function must be derived with respects to the wavelength λ.

By using the product rule and setting the derivative equal to zero, we get

This equation will only be zero if the term in the round bracket becomes zero

This equation can only be solved numerically, e.g., with the Newton’s method. The result will be x = 4,9651. With this result the wavelength λmax can be determined as a function of the temperature by rearranging the equation.

The maximum of the spectral intensity can also be determined for the frequency form Is(f). For this the function Is(f) must be derived with respect to frequency f and setting the derivative equal to zero:

Q12) Derive expression for thermal conductivity of a metal?

A12) Consider two cross-sections A and B in a uniform metallic rod AB separated by a distance λ. Let A at a high temperature (T) and B at low temperature (T-dT).  Now heat conduction takes place from A and B by the electrons. The conduction electron per unit volume is n and average velocity of these electrons is v. During the movement of electrons in the rod, collision takes place. Hence, the electrons near A lose their kinetic energy while electrons near B gain kinetic energy.

At A, average kinetic energy of an electron =kT     ………. (1)

At B, average kinetic energy of the electron =k(T-dT) ………. (2)

The excess of kinetic energy carried by the electron from A to B is

= kdT       ………. (3)

Number of electrons crossing per unit area per time from A and B is

= n   ………. (4)

The excess of energy carried form (A to B) per unit area in unit time is

= n kdT    ………. (5)

Similarly, the deficient of energy carried from B to A per unit area per unit time is

= n kdT    ………. (6)

Hence, the net amount of energy transferred from A to B per unit area per unit time is = n kdT    ………. (7)

But from the basic definition of thermal conductivity, the amount of heat conducted per unit area per unit time is

   ……….. (8)

We know that for the metals

……….. (9)

Substituting (9) in (8)

Also, according to Wiedemann –Franz law; The law states that the ratio of thermal conductivity to electrical conductivity of the metal is directly proportional to the absolute temperature of the metal.

Q13) Derive expression for rectilinear flow of heat through a rod?

A13) Consider a metal rod heated at one end, the isothermal surfaces being parallel planes perpendicular to the length of the rod, and let the axis of x he normal to these planes.

At a distance x from the hot end, let θ he the temperature and d θ /dx be the temperature gradient and consider a layer of thickness dx at this point.

 The amount of heat Qi which enters the layer per second is ……. (1)

Q2 the heat which leaves the layer at the face x ± dx is

(θ+)   ……. (2)

Since θ+ is the temperature of that face. Hence the gain of heat by the layer is equal to

(θ+)] =    ……. (3)

Figure: Flow of heat in a rod

Now before the steady state is reached this amount of heat raises the temperature of the layer of thickness dx. Let p be the density and c the specific heat of the material per unit mass, and let the rate of rise of temperature be denoted by The mass of the layer , hence neglecting the heat lost by radiation from the surface

   …….. (4)

Where h= Thus h is equal to the thermal conductivity divided by the thermal capacity per unit volume. This constant h has been called thermal diffusivity by Kelvin and thermometric conductivity by Maxwell but the former term is more commonly used.

It will be seen that the thermal diffusivity h represents the change of temperature produced in unit volume of the substance by the quantity of heat which would flow in unit time through unit area under unit temperature gradient. Thus, for calculations of the rate of rise of temperature the constant h is of greater importance than K.

 As equation shows (as the rate depends not only on K but also on ), but in the steady state the rate of flow of heat depends only on K and not on

If, in addition, the sides of the bar are allowed to lose heat by radiation, this must be taken into account. If E is the emissive power of the surface, p its perimeter and the excess* of the temperature of the surface over that of the surroundings, this radiation loss Q3 assuming Newton's law of Cooling to hold true, is equal . Hence, we should rewrite it as

    …….. (5)

      …….. (6)

Where

This is the standard Fourier equation for one dimensional flow of heat and any problem in thermal conduction along a rod consists simply in the solution of this differential equation.

Q14) Derive expression for rectilinear flow of heat through a rod for steady state?

A14) Consider a metal rod heated at one end, the isothermal surfaces being parallel planes perpendicular to the length of the rod, and let the axis of x he normal to these planes.

At a distance x from the hot end, let θ he the temperature and d θ /dx be the temperature gradient and consider a layer of thickness dx at this point.

 The amount of heat Qi which enters the layer per second is ……. (1)

Q2 the heat which leaves the layer at the face x ± dx is

(θ+)   ……. (2)

Since θ+ is the temperature of that face. Hence the gain of heat by the layer is equal to

(θ+)] =    ……. (3)

Figure: Flow of heat in a rod

Now before the steady state is reached this amount of heat raises the temperature of the layer of thickness dx. Let p be the density and c the specific heat of the material per unit mass, and let the rate of rise of temperature be denoted by The mass of the layer , hence neglecting the heat lost by radiation from the surface

   …….. (4)

Where h= Thus h is equal to the thermal conductivity divided by the thermal capacity per unit volume. This constant h has been called thermal diffusivity by Kelvin and thermometric conductivity by Maxwell but the former term is more commonly used.

It will be seen that the thermal diffusivity h represents the change of temperature produced in unit volume of the substance by the quantity of heat which would flow in unit time through unit area under unit temperature gradient. Thus, for calculations of the rate of rise of temperature the constant h is of greater importance than K.

 As equation shows (as the rate depends not only on K but also on ), but in the steady state the rate of flow of heat depends only on K and not on

If, in addition, the sides of the bar are allowed to lose heat by radiation, this must be taken into account. If E is the emissive power of the surface, p its perimeter and the excess* of the temperature of the surface over that of the surroundings, this radiation loss Q3 assuming Newton's law of Cooling to hold true, is equal . Hence, we should rewrite it as

    …….. (5)

      …….. (6)

Where

This is the standard Fourier equation for one dimensional flow of heat and any problem in thermal conduction along a rod consists simply in the solution of this differential equation.

A state is said to be stationary when temperature at any point on the rod is stationary i.e.,

We have then

     …….. (7)

Where    ……. (8)

If the radiation losses from the sides can be neglected then this equation is further reduces to

     …….. (9)

The solution of the differential equation yields

     …….. (10)

where the constants A and B can be determined by the boundary conditions

Let these conditions be

at x =0,

is temperature of the source.

at x =l,

is temperature of the source.

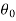
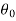
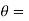
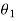
    …….. (11)

is the temperature at any point on x. If the radiation loses are not negligible, solution will be different. Let us assume that in this case is the solution. Hence by substitution,

   …….. (12)

Therefore, the complete solution is

   …….. (13)

Q15) Derive expression radial flow of heat through a spherical shell?

A15) The simplest case of heat conduction in three dimensions is that of a sphere. If the source of heat is placed at the centre of the sphere the isothermal surfaces will be spherical surfaces described about the centre. The method has been employed by Nusselt and others. Nusselt's apparatus is shown in Figure.

Figure: Nusselt's apparatus

The external hollow sphere A is 30 cm. in diameter and made of copper. Inside it and concentric with it, is another hollow sphere C of aluminium, 15 cm. in diameter. The spheres can be split into two and reunited. The space between the spheres is filled with the material B under test such as asbestos, powdered cork, charcoal etc. An electrically heated body D is placed at the centre of the sphere inside C and electrical energy is supplied at a constant rate. Temperatures are determined by means of thermo-couples placed in B at different distances from the centre and along one or more radii. Knowing the electrical energy spent and the radii Fig of the shells, the conductivity can be calculated.

We shall solve the problem from elementary principles. On account of the symmetry about the centre the isothermal surfaces are spherical. The flux of heat across a spherical surface of radius r outwards in unit time is . this must be equal to the amount of electrical energy Q provided per second to the heating body.

Hence,

.   …….. (1)

Or    ……. (2)

Since Q is independent of r, we have

   …….. (3)

Where A is constant of integration

If the two surfaces of the shell have radius r1 and r2 acquire temperature θ1 and θ2 in the steady state, we have

   …….. (4)   ……. (5)

Where =   ……. (6)

Knowing value of Q, θ1, θ2 conductivity can be calculated. Solving the simultaneous equation for A and Q and substituting the value of Q and A, temperature distribution of material can be calculated and it is given as

   …….. (7)

Q16) On what factors conductivity depends?

A16) Thermal conduction is the transfer of heat from one part of a body to another with which it is in contact. Thermal conductivity is defined as ability of material to transmit heat and it is measured in watts per square metre of surface area for a temperature gradient of 1 K per unit thickness of 1 m. The thermal conductivity is not always constant.

The main factors affected the thermal conductivity are the density of material, moisture of material and ambient temperature.  With increasing density, moisture and temperature the thermal conductivity increases too.  Important is inner structure of materials.    Metals and other dense solid materials tend to have high levels of conductivity, whereas materials with very small amount of solid matter and large proportion of voids (gas or air bubbles, not large enough to carry heat by convection) have the lowest thermal conductivities.

Q17) How can we determine thermal conductivity by using Searle’s apparatus?

A17) The definition of conductivity from equation provides a simple method of determining the conductivity of a substance. We need have only a slab of the material of known cross-section heated at one end, and measure the amount of heat that flows out at the other end in a known time, as well as the temperature of the two faces. Hence K can be evaluated.

The method though simple presents considerable experimental difficulties. It is difficult to measure accurately the temperature of the two faces of a slab of metal. This is best achieved by keeping embedded in the surface the junction of a thermocouple, the use of mercury thermometer or resistance thermometer being inconvenient or impossible. Some early experimenters used steam to heat the slab at one end and ice or water to cool it at the other end, and assumed that the temperature of the end faces of the slab was that of steam and water respectively. But if proper precautions be not taken, the method sometimes gives absurd results. This is on account of the fact that a thin film of fluid always at rest, is formed in contact with the surface, and this has a large temperature gradient. Hence it is essential that we should observe the temperature inside the slab itself by means of thermometers. There are many apparatus based on this method, and one due to Searle is described below. Figure 4 shows the apparatus diagrammatically.

Figure: Searle’s apparatus

One end B of the rod AB is enclosed in the steam-chamber S while the other end A projects into another chamber C through which cold water circulates as indicated, the temperatures at entry and exit being T3 and T4 respectively. Temperatures at two points along the bar are measured by thermometers T1 and T2; let these be T1 and T2. The whole rod is wrapped round with some non-conducting material like wood, felt, etc. In the steady state if m grams of water flow past the cold end of the bar per second, the heat conducted by the bar per second is equals to the

Where d is the distance between the thermometer T1 and T2, thus conductivity k can be determined.

Q18) What are the limitation in Searle’s apparatus and how is it overcome?

A18) In the Searle’s experiment some heat was lost by radiation outflow from the side of bar. But this can be easily eliminated if the bar is surrounded by some material at same temperature as to adjacent portion of bar.

There will be no flow of heat perpendicular to the length of the bar as no temperature gradient exists in that direction. Surrounded material is called guard ring.

Q19) How Berget utilised this guard-ring method for determining the conductivity?

A19) Berget utilised this guard-ring method for determining the conductivity of various substances such as copper, iron, brass and mercury. A vertical cylindrical column of mercury is surrounded by an annular ring of mercury. In both the upper surface of mercury is heated by steam while the lower surface rests on a metal plate cooled by ice. Thus, the temperature gradient as well as the temperatures at the same level in the experimental column and the surrounding annular ring is identical.

Under these conditions there can be no lateral flow of heat and the annular ring serves as a 'guard-ring'. The lower end of the experimental column projects into the bulb of a Bunsen ice-calorimeter and the heat flowing out at the lower end is found from the indications of the mercury thread.

The difference of temperature between several points along the column is determined by four differential thermo-couples. The conductivity K can be calculated from formula.

This method has been adopted by a number of workers, notably by Lees, Donaldson, Honda and Simidu, and others.

Lees used the rod method for measuring the conductivity of many metals throughout the temperature range 18°C to — 170°C. The experimental rod, about 7 cm. long and 0.58 cm. in diameter, was heated electrically at the upper end, its lower end being X-fixed to the base of a hollow, closed, cylindrical shell of copper which completely surrounded the rod. The outer cylinder was suspended inside a Dewar flask and immersed in liquid air or heated electrically and thus the desired temperature of experiment was attained

Knowing the value of electrical energy spent in heater wire and the temperature at point on the rod by using platinum resistance thermometer, thermal conductivity can be calculated.

Honda and simidu employed two plate method shown in figure. P1 and P2 are exactly similar plate made of the experimental material. Between these two a symmetrical placed heater H in which Q heat is generated. For perfect symmetry two cold plates, K maintained at same temperature are placed at the other end of these plates. The amount of heat flow through each plate is Q/2.

Figure: The two-plate system

Q20) Explain and derive Kirchhoff's Law?

A20) We know that emission and absorption vary together. In 1859, Kirchhoff* deduced an important law which may be stated as follows: -

“At a given temperature the ratio of the emissive power to the absorptive power is the same for all substances and is equal to the emissive power of a perfectly black body”.

Though this law was first recognised by Balfour Stewart, Kirchhoff was the first to deduce it from thermodynamical principles, and apply it in all directions. It is therefore usually known as Kirchhoff's law. We have considered here the total emission regardless of wave-length but the same relation holds for each wavelength separately. Thus, for radiations of the same wavelength and the same temperature, the ratio of the emissive and absorptive powers for all bodies is the same and equal to the emissive power of a perfectly black body. This also holds for each plane polarised component of any ray.

Deduction of Kirchhoff's Law

Suppose we have a uniformly heated enclosure containing some substance whose emissive and absorptive powers for radiation of wavelength lying between λ and λ +dλ are eλ and aλ respectively.

We know the amount of radiation dQ falling on the substance from the walls does not depend upon the nature or the shape of the walls. Of this a portion aλdQ is absorbed by the substance while the remainder (1 – aλ) dQ is reflected or transmitted. Further the substance will emit radiation equal to eλ dλ by virtue of its temperature. Equating the energy absorbed to the energy emitted we have

eλdλ = aλdQ   ………. (1)

In the case of a perfectly black body of emissivity E λ we have (since aλ = 1),

Eλdλ = aλdQ   ………. (2)

Combining (1) and (2) we get

eλ/aλ = Eλ    ………. (3)

i.e., at any temperature the ratio of the emissive power to the absorptive power of a substance is constant and equal to the emissive power of a perfectly black body. This is the thermodynamic proof of Kirchhoff's law.

We have proved the law here for bodies inside the enclosure. Now since the emissive and absorptive powers depend only upon the physical nature of the body and not upon its surroundings, it follows that the law will hold for all bodies under all conditions for pure temperature radiation.

Q21) Write Applications of Kirchhoff's Law?

A21) The law embodies two distinct relations, a qualitative and a quantitative one. Qualitatively, it implies that if a body is capable of emitting certain radiations it will absorb them when they fall on it.

Quantitatively, it signifies that the ratio is the same for all bodies. Various experimental proofs and observations may be cited in support of the qualitative relation. If a piece of decorated china is heated in a furnace to about 1000°C and then taken out suddenly in a dark room, the decorations appear much brighter than the white china, because these being better absorbers, emit also much greater light.

If we take a polished metal ball and have a black spot on it by coating it with platinum black, then on heating the ball to about 1000°C and suddenly taking it out in a dark room, it will he found that the black spot is shining much more brilliantly than the polished surface.

Again, take the case of a coloured glass. We know that green glass looks green because it absorbs red light strongly and reflects the green (red and green being complementary colours). Hence when a piece of green glass is heated in a furnace and then taken out, it is found to glow with a red light. Similarly, a piece of red glass is found to glow with green light.

A more decisive example illustrating selective action is that of erbium oxide, didymium oxide, etc., which when heated emit certain bright bands in addition to the continuous spectrum. If now a solution of these oxides is made and continuous light is passed through it, the very same bands appear in absorption.