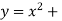Unit - 3
Applications of single and Multiple integration
Q1) Determine the area enclosed by the curves-

A1)
We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-

Which gives-

By factorization,

Which means,
x = 2 and x = -3
By determining the intersection points the range the values of x have been found-
x | -3 | -2 | -1 | 0 | 1 | 2 |
| 10 | 5 | 2 | 1 | 2 | 5 |
And
x | -3 | 0 | 2 |
y = 7 - x | 10 | 7 | 5 |
We get the following figure by using above two tables-

Area of shaded region = 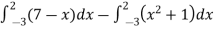

= 

= (12 – 2 – 8/3) – (-18 – 9/2 + 9)
= 
= 125/6 square unit
Q2) Find the area enclosed by the two functions-
 and g(x) = 6 – x
and g(x) = 6 – x
A2)
We get the following figure by using these two equations
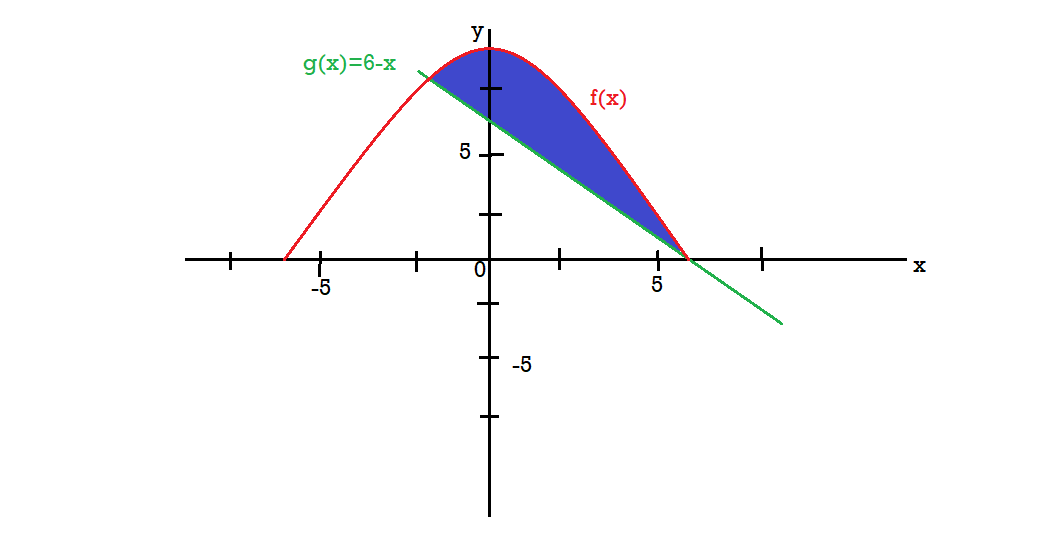
To find the intersection points of two functions f(x) and g(x)-
f(x) = g(x)




On factorizing, we get-
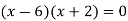
x = 6, -2
Now

Then, area under the curve-
A = 



Therefore, the area under the curve is 64/3 square unit.
Q3) Find the area enclosed by the curves  and if the area is rotated
and if the area is rotated  about the x-axis, then determine the volume of the solid of revolution.
about the x-axis, then determine the volume of the solid of revolution.
A3)
We know that, at the point of intersection the coordinates of the curve are equal. So that first we will find the point of intersection-



We get,
x = 0 and x = 2
The curve of the given equations will look like as follows-
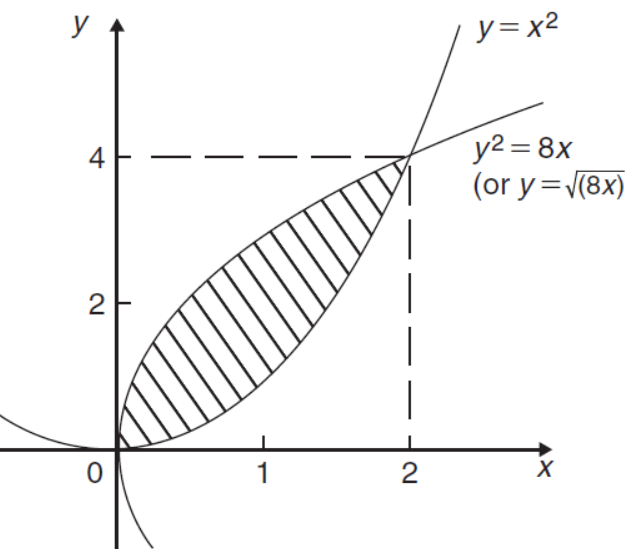
Then,
The area of the shaded region will be-
A = 
So that the area will be 8/3 square unit.
The volume will be
= (volume produced by revolving  – (volume produced by revolving
– (volume produced by revolving 
= 
Q4) Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1, 3].
A4)
The graph of the function f(x) = 1/x will look like-

The volume of the solid of revolution generated by revolving R (violet region) about the y-axis over the interval [1, 3]
Then the volume of the solid will be-


Q5) Evaluate  , where dA is the small area in xy-plane.
, where dA is the small area in xy-plane.
A5)
Let, I = 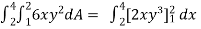
= 
= 
= 
= 84 sq. unit.
Which is the required area,
Q6) Evaluate the following double integral,
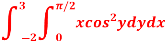
A6)
Let,
I = 
On solving the integral, we get

Q7) Change the order of integration in the double integral-
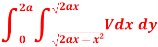
A7)
Limits are given-
x = 0, x = 2a

And

and


The area of integration is the shaded portion of OAB. On changing the order of integration first we will integrate with respect to x, the area of integration has three portions BCE, ODE and ACD,

Now-

Which is the required answer.
Q8) Express as single integral and evaluate dy dx + dy dx.
A8)
Given: I = dy dx + dy dx
I = I1 + I2

The limits of region of integration I1 are
x = – ; x = and y = 0, y = 1 and I2 are x = – 1,
x = 1 and y = 1, y = 3.
The region of integration is as shown in Fig. 6.7
To consider the complete region take a vertical strip SR along the strip y varies from y = x2 to
y = 3 and x varies from x = –1 to x = 1. Fig. 6.7
I = 

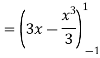

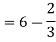

Q9) Evaluate the following by changing to polar coordinates,

A9)
In this problem, the limits for y are 0 to  and the limits for are 0 to 2.
and the limits for are 0 to 2.
Suppose,
y = 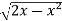
squaring both sides,
y² = 2x - x²
x² + y² = 2x
but in polar coordinates,
we have,
r² = 2r cosθ
r = 2 cosθ
from the region of integration, r lies from 0 to 2 cosθ and θ varies from 0 to π / 2.
As we know in case of polar coordinates,
Replace x by r cosθ and y by r sinθ, dy dx by r drdθ,
We get,

Q10) Evaluate 
A10)
Let the integral,
I = 
=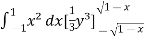

Put x = sinθ

= π / 24 ans.
Q11) Find the area enclosed by two curves using double integration.
y = 2 – x and y² = 2 (2 – x)
A11)
Let,
y = 2 – x ………………... (1)
and
y² = 2 (2 – x) ………………... (2)
on solving eq. (1) and (2)
we get the intersection points (2,0) and (0,2),
we know that,
Area = 

Here we will find the area as below,
Area = 


Which gives,
= (- 4 + 4 /2) + 8 / 3 = 2 / 3.
Q12) Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.
A12)
We have,
r = a(1+cosθ) ……………………. (1)
and
r = a ………………………………. (2)
on solving these equations by eliminating r, we get
a(1+cosθ) = a
(1+cosθ) = 1
cosθ = 0
here a θ varies from – π/2 to π/2
limit of r will be a and 1+cosθ)

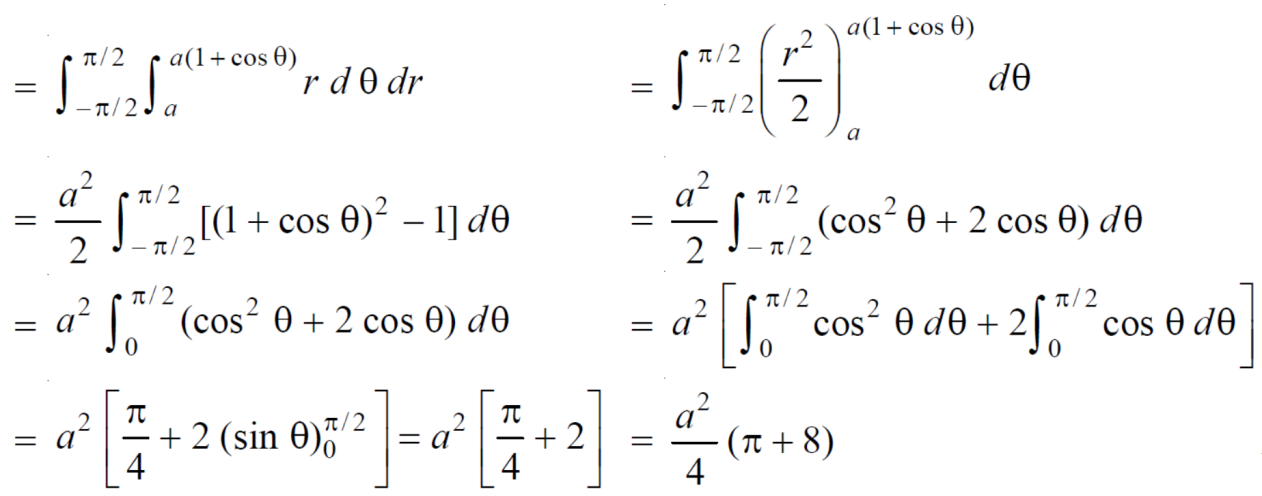
Which is the required area.
Q13) Find the are lying inside a cardioid r = 1 + cosθ and outside the parabola r (1 + cosθ) = 1.
A13)
Let,
r = 1 + cosθ ……………………... (1)
r (1 + cosθ) = 1……………………... (2)
solving these equations, we get
(1 + cosθ) (1 + cosθ) = 1
(1 + cosθ) ² = 1
1 + cosθ = 1
cosθ = 0
θ = ±π / 2
so that, limits of r are,
1 + cosθ and 1 / 1 + cosθ
The area can be founded as below,



Q14) Find the volume generated by revolving a circle x ² + y² = 4 about the line x= 3.
A14)
We know that,
Volume = 
Here , PQ = 3 – x,
= 

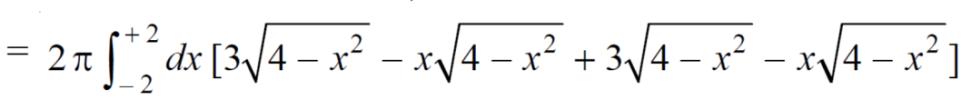

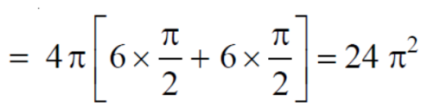
The volume is 24π².
Q15) Evaluate

A15)
Let
I = 
= 
(Assuming m =  )
)
=  dxdy
dxdy
= 
=
=  dx
dx
=  dx
dx
= 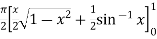
=
I =
Q16) Find Volume of the tetrahedron bounded by the co-ordinate’s planes and the plane

A16)
Volume = ………. (1)
………. (1)
Put  ,
, 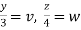

From equation (1) we have
V = 
=24
=24 (u+v+w=1) By Dirichlet’s theorem.
(u+v+w=1) By Dirichlet’s theorem.
=24 
=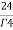 =
= = 4
= 4
Volume =4
Q17) Evaluate-
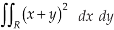
Where-
R is the region bounded by a parallelogram- x + y = 0, x + y = 2, 3x – 2y = 0, 3x – 2y = 3.
A17)
By changing the variables x, y to the new variables u and v, by the substitution x + y = u, 3x – 2y = v, the given parallelogram R reduces to a rectangle 



The required Jacobian is-

Since u = x + y and u = x + y = 2, here u varies from 0 to 2 while v varies from 0 to 3.
Since-
3x – 2y = v = 0, 3x – 2y = v = 3
Therefore, the integral will be in new variables-
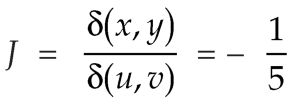


Which is the required answer.
Q18) Evaluate  dx.
dx.
A18)
Let 
 dx.
dx.
Put  or
or  ; 4x dx = dt
; 4x dx = dt
x | 0 |
|
t | 0 |
|
 dx
dx
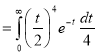



Q19) Evaluate I = 
A19) 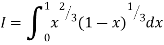
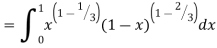

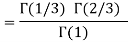



= 2 π/3
Q20) Show that
A20)
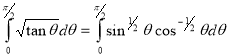
=
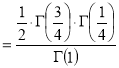


 (
(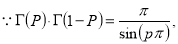 0<p<1)
0<p<1)



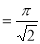 (By above result)
(By above result)