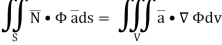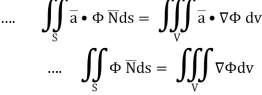Unit - 4
Vector calculus
Q1) Define vector function.
A1)
Vector function-
Suppose  be a function of a scalar variable t, then-
be a function of a scalar variable t, then-
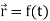
Here vector 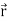 varies corresponding to the variation of a scalar variable t that its length and direction be known as value of t is given.
varies corresponding to the variation of a scalar variable t that its length and direction be known as value of t is given.
Any vector 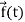 can be expressed as-
can be expressed as-

Here 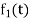 ,
,  ,
,  are the scalar functions of t.
are the scalar functions of t.
Q2) A particle moves along the curve  , here ‘t’ is the time. Find its velocity and acceleration at t = 2.
, here ‘t’ is the time. Find its velocity and acceleration at t = 2.
A2)
Here we have-

Then, velocity

Velocity at t = 2,
= 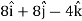
Acceleration = 
Acceleration at t = 2,

Q3) If  and
and  then find-
then find-
1. 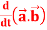
2. 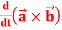
A3)
We know that-
1.

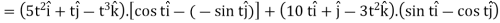


2.

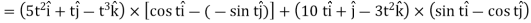

Q4) If  , then show that
, then show that
1. 
2. 
A4)
1. Suppose 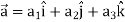 and
and 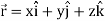

Now taking L.H.S,
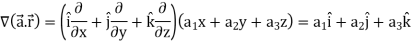
Which is 
Hence proved.
2. 
So that

Q5) If  then find grad f at the point (1, -2, -1).
then find grad f at the point (1, -2, -1).
A5)
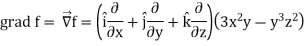


Now grad f at (1, -2, -1) will be-


Q6) If  then prove that grad u, grad v and grad w are coplanar.
then prove that grad u, grad v and grad w are coplanar.
A6)
Here- 


Now-
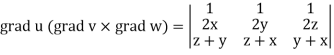

Apply 
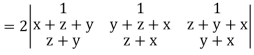

Which becomes zero.
So that we can say that grad u, grad v and grad w are coplanar vectors.
Q7) Find the directional derivative of 1/r in the direction  where
where 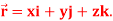
A7)
Here 
Now,
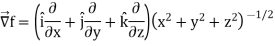



And 
We know that-
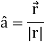
So that-

Now,
Directional derivative-

Q8) Find the directional derivative of

At the points (3, 1, 2) in the direction of the vector  .
.
A8)
Here it is given that-


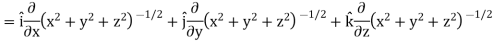


Now at the point (3, 1, 2)-

Let  be the unit vector in the given direction, then
be the unit vector in the given direction, then
 at (3, 1, 2)
at (3, 1, 2)
Now,

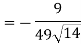
Q9) Show that 
A9)


Interchanging  , we get-
, we get-

We get by using above equations-

Q10) Prove that 
A10)

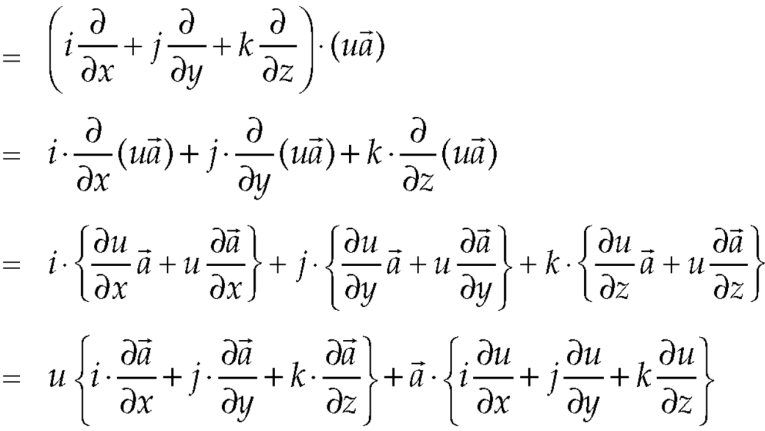
So that-

Q11) Prove that 
A11)

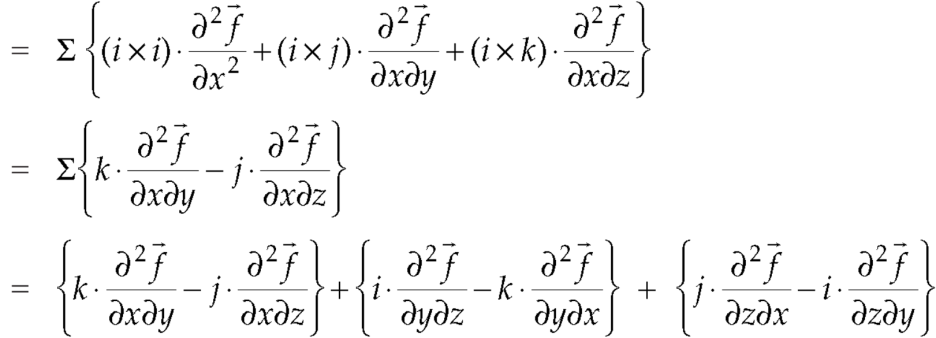
So that-

Q12) If  then find the divergence and curl of
then find the divergence and curl of  .
.
A12)
We know that-

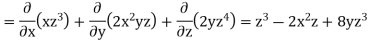
Now-

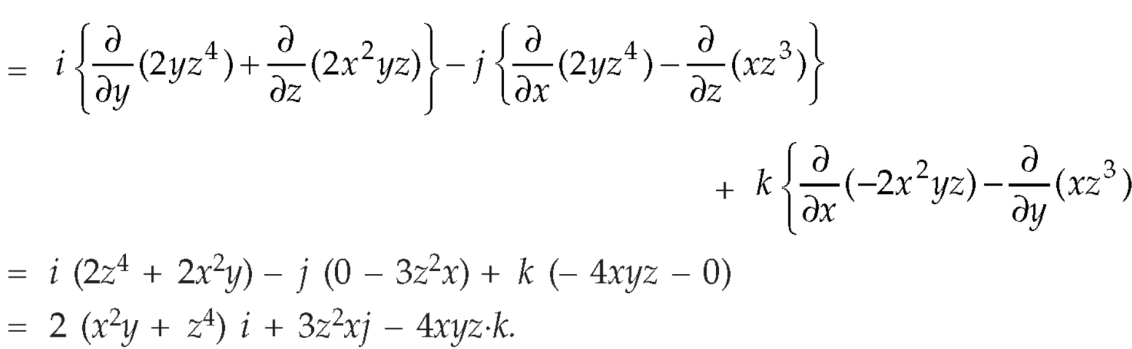
Q13) Prove that 
A13)
here  and
and 
So that

Now-



So that-

Q14) Evaluate  where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y= in the xy plae from (1,0) to (0,1)
in the xy plae from (1,0) to (0,1)
A14)
The curve y= i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
 =
= 
= 
= =-1
=-1
Q15) Evaluate  where
where  = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
A15)
F x dr = 
Put x=t, y=t2, z= t3
Dx=dt, dy=2tdt, dz=3t2dt.
F x dr = 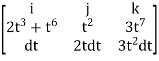
=(3t4-6t8) dti – (6t5+3t8 -3t7) dt j +( 4t4+2t7-t2) dt k
= t4-6t3) dti –(6t5+3t8-3t7) dt j+(4t4 + 2t7 – t2) dt k
t4-6t3) dti –(6t5+3t8-3t7) dt j+(4t4 + 2t7 – t2) dt k
=
= +
+
Q16) Prove that ͞͞͞F = [y2cos x +z3] i+(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞ F (ii) the work done in moving an object in this field from (0, 1, -1) to ( / 2, -1, 2)
/ 2, -1, 2)
A16)
(a) The field is conservative if cur͞͞͞͞͞͞F = 0.
 Now, curl͞͞͞ F =
Now, curl͞͞͞ F = 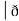 ̷̷
̷̷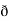 X
X 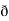 /
/ 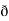 y
y 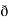 /
/  z
z
Y2COS X +Z3 2y sin x-4 3xz2 + 2
; Cur  = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =
(y2cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =  i +
i +  j +
j +  k
k
 = y2cos x + z3,
= y2cos x + z3, 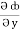 = 2y sin x – 4,
= 2y sin x – 4,  = 3xz2 + 2
= 3xz2 + 2
Now,  =
=  dx +
dx +  dy +
dy + 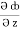 dz
dz
= (y2cos x + z3) dx +(2y sin x – 4) dy + (3xz2 + 2) dz
= (y2cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d (y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =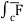 .d ͞r
.d ͞r
=  dx + (2y sin x – 4) dy + (3xz2 + 2) dz
dx + (2y sin x – 4) dy + (3xz2 + 2) dz
=  (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z] ( 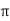 /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4] – {- 4 – 2} =4
+ 4 + 4] – {- 4 – 2} =4 + 15
+ 15
Q17) Evaluate  , where S is the surface of the sphere
, where S is the surface of the sphere  in the first octant.
in the first octant.
A17)
Here-
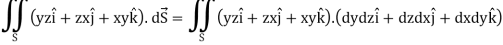



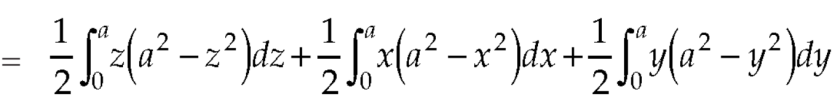

Which becomes-

Q18) Verify stoke’s theorem when  and surface S is the part of sphere
and surface S is the part of sphere  , above the xy-plane.
, above the xy-plane.
A18)
We know that by stoke’s theorem,
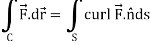
Here C is the unit circle- 


So that-
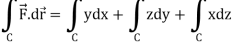
Now again on the unit circle C, z = 0
dz = 0
Suppose, 
And 
Now
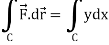

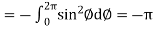 ……………… (1)
……………… (1)
Now-
Curl 
Using spherical polar coordinates-
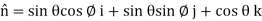


 ………………… (2)
………………… (2)
From equation (1) and (2), stoke’s theorem is verified.
Q19) Verify Stoke’s theorem for the given function-

Where C is the unit circle in the xy-plane.
A19)
Suppose-


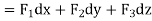
Here 
We know that unit circle in xy-plane-
Or

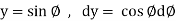
So that,
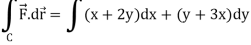
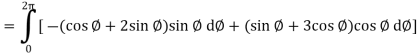



Now
Curl 
Now,
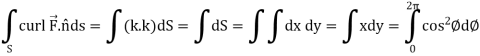
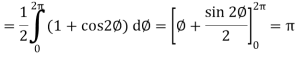
Hence the Stoke’s theorem is verified.
Q20) Show that 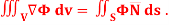
A20)
By divergence theorem, 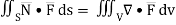 ...… (1)
...… (1)
Comparing this with the given problem let

Hence, by (1)
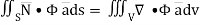 …………. (2)
…………. (2)
Now,
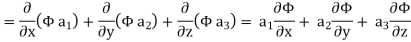
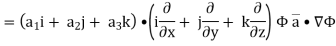
Hence, from (2), We get,