Unit 1
Ratio Proportion
Q1)- If Rs. 74000 are to be divided among three people X, Y and Z such that X: Y = 4: 5 and Y: Z = 3: 2 then what amount each person will receive?
A1)-
Here X: Y: Z: = 12:15:10
Here sum of the ratio is = 12 + 15 + 10 = 37
Then-
X will get = 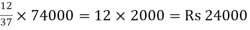
Y will get = 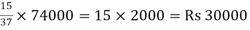
Z will get = 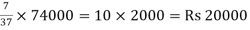
Q2)- A and B are partners sharing profits in the ratio of 3:2. A new partner, C is admitted for a one-sixth share in the future profit. Calculate new profit and sacrificing ratio.
A2)-
Computation of New profit ratio and Sacrifice ratio: –
Old ratio among A and B is 3:2
Share of New partner, C is 1/6
Remaining future share for A and B = 1 – 1/6 = 5/6
(This needs to be shared among A and B in 3:2)
Thus,
A’s new share = 5 /6 × 3/5 = 3/6
B’s new share = 5 /6 × 2/5 = 2/6
And C’s share is already given as 1/6
Hence, New Profit ratio among A:B:C is 3:2:1
Here, the Sacrifice ratio among A and B is 3:2
(as they sacrifice in old ratio for share of new Partner)
Q3)- A and B are partners sharing profits in the ratio of 5:3. C is admitting into partnership and for this purpose, A is surrendering two eighths from his share and B surrendered one eighth from his share in favour of C. Calculate New profit-sharing ratio.
A3)-
Computation of New profit ratio and Sacrifice ratio
Old ratio among A and B is 5:3
New share of each partner is as under:
A’s new share = 5/8 – 2/8 = 3/8
B’s new share = 3/8 – 1/8 = 2/8
C’s new share = 2/8+1/8 = 3/8
Thus, new profit ratio among A:B:C is 3:2:3
The Sacrifice ratio among A and B is as under:
A surrendered = 2/8
B surrendered = 1 /8
Hence, Sacrifice ratio is 2:1
Q4)-A and B are partner sharing profits in the ratio of 3:2. A new partner has been admitted to the partnership. A surrendered one-third of his share and B surrendered one half of his share in favour of C. Calculate sacrificing ratio.
A5)-
Computation of New profit ratio and Sacrifice ratio
Old ratio among A and B is 3:2
Sacrifice ratio among A and B is computed as under:
A surrendered = 3/5 × 1/3 = 1/5
B surrendered = 2/5 × 1/2 = 1/5
Here, Sacrifice ratio among A and B is 1:1
Now, New profit-sharing ratio is computed as under:
A’s new share = 3/5 – 1/5 = 2/5
B’s new share = 2/5 – 1/5 = 1/5
C’s share = 1/5 + 1/5 = 2/5
Hence, New ratio among A:B:C is 2:1:2
Q5)-Amit, Sumit, and Punit share profit and losses in the ratio of 3:2:1, respectively. Amit retires and the remaining partners decide to share to take Amit’s share in the existing ratio i.e., 2:1. Calculate the new ratio and gaining ratio.
A6)-
The existing ratio between Sumit and Punit= 2/6 and 1/6
Amit’s ratio (retiring partner) = 3/6
Amit’s share taken by Sumit and Punit in the ratio of 2:1
Sumit gets = 3/6 * 2/3 = 6/18
Punit gets = 3/6 * 1/3 = 3/18
New ratio between Sumit and Punit is = 6:3 = 2:1
Gaining ratio= New Ratio – Old Ratio
Sumit’s gain = 2/3 – 2/6 = 2/6
Punit’s gain = 1/3 – 1/6 = 1/6
Gaining ratio = 2:1
New Ratio = 2:1
Q6)-10 men working 8 hours a day can finish a work in 12 days. In how many days can 12 men working 5 hours a day finish the same work?
A7)-
This can be arranged as-

Then
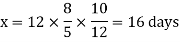
Q7)-Two numbers are in the ratio of 3: 5 and if 10 be subtracted from each of them, the remainders are in the ratio of 1: 5, find the numbers.
A8)-
Let the numbers be x and y, so that- x/y =3/5 or 5x = 3y … (1)
Again-
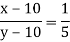
Or
5x – y = 40… (2)
By solving (1) and (2), we get-
X = 12 and y = 20
Hence the required numbers are- 12 and 20
Q8)- The prime cost of an article was three times the value of material used. The cost of raw materials was increased in the ratio 3: 4 and the productive wage was increased in the ratio 4: 5. Find the present prime cost of an article, which could formerly be made for Rs.180.
A9)-
Prime cost = x + y, where x = productive wage, y = material used
Now prime cost = 180 =3y or, y = 60, again x + y = 180, x = 180–y = 180–60 = 120
Present material cost = 4y/3 and present wage = 5x / 4
Present prime cost–
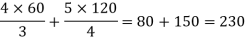
Hence the present prime cost is Rs. 230.
Q9)-A machine in a drinking water supplying factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
A10)-
Let the bottles filled by machine in 5 hours be x
We can write the given information as follows-
Number of bottles | Tine taken (in hrs) |
840 | 6 |
X | 5 |
There is a direct relationship between time taken and bottles filled by machine,
So that, we get-
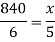
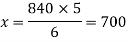
So that 700 bottles can be filled by the machine in 5 hrs.
Q10)-In a model of a ship, the mast is 9 m high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?
A11)-
Suppose the mast of the model ship be x, then
We can write the given information as follows-
| Height of mast | Length of ship |
Model ship | 9 m | x |
Actual ship | 12m | 28m |
There is a direct relationship-
So that,
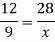

So that the length of a model ship is 21m.
Q11)-10 men can do a piece of work in 30 days then in how many days 20 men can do the same work?
A12)-
Let ‘x’ days be taken to do the task,
Then
Men | Days |
10 | 30 |
20 | X |
There is inverse relationship, so that-
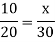
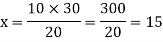
So that 20 men can do the same piece of work in 15 days.
Q12)-A person has a monthly salary of Rs. 20,000. He spends 8000 per month on food then what percent of his monthly salary does he save?
A13)-
Person’s monthly salary = 20,000
Savings = (20,000 – 8000) = 12,000
Fraction of his saving = 12,000/20,000
By converting the fraction into percentage, we get-
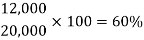
Q13)-A shopkeeper reduced the price of an item by 25%, the old price was 120 then find out the new price.
A14)-
25% of 120 will be-
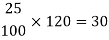
Which means he reduced Rs. 30, then the new price is-
120 – 30 = 90
The new price is Rs. 90
Q14)-If 20% of any number is 500 then find out the number?
A15)-
Let the number is ‘x’, then-
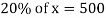
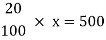
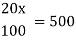
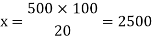
Hence the number is 2500.
Decrease in number = Original number – New number
Unit 1
Ratio Proportion
Q1)- If Rs. 74000 are to be divided among three people X, Y and Z such that X: Y = 4: 5 and Y: Z = 3: 2 then what amount each person will receive?
A1)-
Here X: Y: Z: = 12:15:10
Here sum of the ratio is = 12 + 15 + 10 = 37
Then-
X will get = 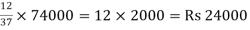
Y will get = 
Z will get = 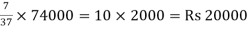
Q2)- A and B are partners sharing profits in the ratio of 3:2. A new partner, C is admitted for a one-sixth share in the future profit. Calculate new profit and sacrificing ratio.
A2)-
Computation of New profit ratio and Sacrifice ratio: –
Old ratio among A and B is 3:2
Share of New partner, C is 1/6
Remaining future share for A and B = 1 – 1/6 = 5/6
(This needs to be shared among A and B in 3:2)
Thus,
A’s new share = 5 /6 × 3/5 = 3/6
B’s new share = 5 /6 × 2/5 = 2/6
And C’s share is already given as 1/6
Hence, New Profit ratio among A:B:C is 3:2:1
Here, the Sacrifice ratio among A and B is 3:2
(as they sacrifice in old ratio for share of new Partner)
Q3)- A and B are partners sharing profits in the ratio of 5:3. C is admitting into partnership and for this purpose, A is surrendering two eighths from his share and B surrendered one eighth from his share in favour of C. Calculate New profit-sharing ratio.
A3)-
Computation of New profit ratio and Sacrifice ratio
Old ratio among A and B is 5:3
New share of each partner is as under:
A’s new share = 5/8 – 2/8 = 3/8
B’s new share = 3/8 – 1/8 = 2/8
C’s new share = 2/8+1/8 = 3/8
Thus, new profit ratio among A:B:C is 3:2:3
The Sacrifice ratio among A and B is as under:
A surrendered = 2/8
B surrendered = 1 /8
Hence, Sacrifice ratio is 2:1
Q4)-A and B are partner sharing profits in the ratio of 3:2. A new partner has been admitted to the partnership. A surrendered one-third of his share and B surrendered one half of his share in favour of C. Calculate sacrificing ratio.
A5)-
Computation of New profit ratio and Sacrifice ratio
Old ratio among A and B is 3:2
Sacrifice ratio among A and B is computed as under:
A surrendered = 3/5 × 1/3 = 1/5
B surrendered = 2/5 × 1/2 = 1/5
Here, Sacrifice ratio among A and B is 1:1
Now, New profit-sharing ratio is computed as under:
A’s new share = 3/5 – 1/5 = 2/5
B’s new share = 2/5 – 1/5 = 1/5
C’s share = 1/5 + 1/5 = 2/5
Hence, New ratio among A:B:C is 2:1:2
Q5)-Amit, Sumit, and Punit share profit and losses in the ratio of 3:2:1, respectively. Amit retires and the remaining partners decide to share to take Amit’s share in the existing ratio i.e., 2:1. Calculate the new ratio and gaining ratio.
A6)-
The existing ratio between Sumit and Punit= 2/6 and 1/6
Amit’s ratio (retiring partner) = 3/6
Amit’s share taken by Sumit and Punit in the ratio of 2:1
Sumit gets = 3/6 * 2/3 = 6/18
Punit gets = 3/6 * 1/3 = 3/18
New ratio between Sumit and Punit is = 6:3 = 2:1
Gaining ratio= New Ratio – Old Ratio
Sumit’s gain = 2/3 – 2/6 = 2/6
Punit’s gain = 1/3 – 1/6 = 1/6
Gaining ratio = 2:1
New Ratio = 2:1
Q6)-10 men working 8 hours a day can finish a work in 12 days. In how many days can 12 men working 5 hours a day finish the same work?
A7)-
This can be arranged as-

Then
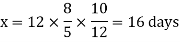
Q7)-Two numbers are in the ratio of 3: 5 and if 10 be subtracted from each of them, the remainders are in the ratio of 1: 5, find the numbers.
A8)-
Let the numbers be x and y, so that- x/y =3/5 or 5x = 3y … (1)
Again-
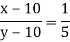
Or
5x – y = 40… (2)
By solving (1) and (2), we get-
X = 12 and y = 20
Hence the required numbers are- 12 and 20
Q8)- The prime cost of an article was three times the value of material used. The cost of raw materials was increased in the ratio 3: 4 and the productive wage was increased in the ratio 4: 5. Find the present prime cost of an article, which could formerly be made for Rs.180.
A9)-
Prime cost = x + y, where x = productive wage, y = material used
Now prime cost = 180 =3y or, y = 60, again x + y = 180, x = 180–y = 180–60 = 120
Present material cost = 4y/3 and present wage = 5x / 4
Present prime cost–
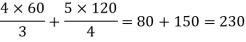
Hence the present prime cost is Rs. 230.
Q9)-A machine in a drinking water supplying factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
A10)-
Let the bottles filled by machine in 5 hours be x
We can write the given information as follows-
Number of bottles | Tine taken (in hrs) |
840 | 6 |
X | 5 |
There is a direct relationship between time taken and bottles filled by machine,
So that, we get-
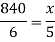
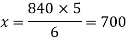
So that 700 bottles can be filled by the machine in 5 hrs.
Q10)-In a model of a ship, the mast is 9 m high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?
A11)-
Suppose the mast of the model ship be x, then
We can write the given information as follows-
| Height of mast | Length of ship |
Model ship | 9 m | x |
Actual ship | 12m | 28m |
There is a direct relationship-
So that,
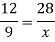
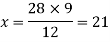
So that the length of a model ship is 21m.
Q11)-10 men can do a piece of work in 30 days then in how many days 20 men can do the same work?
A12)-
Let ‘x’ days be taken to do the task,
Then
Men | Days |
10 | 30 |
20 | X |
There is inverse relationship, so that-
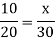

So that 20 men can do the same piece of work in 15 days.
Q12)-A person has a monthly salary of Rs. 20,000. He spends 8000 per month on food then what percent of his monthly salary does he save?
A13)-
Person’s monthly salary = 20,000
Savings = (20,000 – 8000) = 12,000
Fraction of his saving = 12,000/20,000
By converting the fraction into percentage, we get-
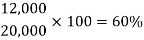
Q13)-A shopkeeper reduced the price of an item by 25%, the old price was 120 then find out the new price.
A14)-
25% of 120 will be-
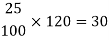
Which means he reduced Rs. 30, then the new price is-
120 – 30 = 90
The new price is Rs. 90
Q14)-If 20% of any number is 500 then find out the number?
A15)-
Let the number is ‘x’, then-
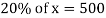
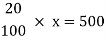
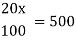
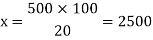
Hence the number is 2500.
Decrease in number = Original number – New number
Unit 1
Unit 1
Ratio Proportion
Q1)- If Rs. 74000 are to be divided among three people X, Y and Z such that X: Y = 4: 5 and Y: Z = 3: 2 then what amount each person will receive?
A1)-
Here X: Y: Z: = 12:15:10
Here sum of the ratio is = 12 + 15 + 10 = 37
Then-
X will get = 
Y will get = 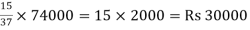
Z will get = 
Q2)- A and B are partners sharing profits in the ratio of 3:2. A new partner, C is admitted for a one-sixth share in the future profit. Calculate new profit and sacrificing ratio.
A2)-
Computation of New profit ratio and Sacrifice ratio: –
Old ratio among A and B is 3:2
Share of New partner, C is 1/6
Remaining future share for A and B = 1 – 1/6 = 5/6
(This needs to be shared among A and B in 3:2)
Thus,
A’s new share = 5 /6 × 3/5 = 3/6
B’s new share = 5 /6 × 2/5 = 2/6
And C’s share is already given as 1/6
Hence, New Profit ratio among A:B:C is 3:2:1
Here, the Sacrifice ratio among A and B is 3:2
(as they sacrifice in old ratio for share of new Partner)
Q3)- A and B are partners sharing profits in the ratio of 5:3. C is admitting into partnership and for this purpose, A is surrendering two eighths from his share and B surrendered one eighth from his share in favour of C. Calculate New profit-sharing ratio.
A3)-
Computation of New profit ratio and Sacrifice ratio
Old ratio among A and B is 5:3
New share of each partner is as under:
A’s new share = 5/8 – 2/8 = 3/8
B’s new share = 3/8 – 1/8 = 2/8
C’s new share = 2/8+1/8 = 3/8
Thus, new profit ratio among A:B:C is 3:2:3
The Sacrifice ratio among A and B is as under:
A surrendered = 2/8
B surrendered = 1 /8
Hence, Sacrifice ratio is 2:1
Q4)-A and B are partner sharing profits in the ratio of 3:2. A new partner has been admitted to the partnership. A surrendered one-third of his share and B surrendered one half of his share in favour of C. Calculate sacrificing ratio.
A5)-
Computation of New profit ratio and Sacrifice ratio
Old ratio among A and B is 3:2
Sacrifice ratio among A and B is computed as under:
A surrendered = 3/5 × 1/3 = 1/5
B surrendered = 2/5 × 1/2 = 1/5
Here, Sacrifice ratio among A and B is 1:1
Now, New profit-sharing ratio is computed as under:
A’s new share = 3/5 – 1/5 = 2/5
B’s new share = 2/5 – 1/5 = 1/5
C’s share = 1/5 + 1/5 = 2/5
Hence, New ratio among A:B:C is 2:1:2
Q5)-Amit, Sumit, and Punit share profit and losses in the ratio of 3:2:1, respectively. Amit retires and the remaining partners decide to share to take Amit’s share in the existing ratio i.e., 2:1. Calculate the new ratio and gaining ratio.
A6)-
The existing ratio between Sumit and Punit= 2/6 and 1/6
Amit’s ratio (retiring partner) = 3/6
Amit’s share taken by Sumit and Punit in the ratio of 2:1
Sumit gets = 3/6 * 2/3 = 6/18
Punit gets = 3/6 * 1/3 = 3/18
New ratio between Sumit and Punit is = 6:3 = 2:1
Gaining ratio= New Ratio – Old Ratio
Sumit’s gain = 2/3 – 2/6 = 2/6
Punit’s gain = 1/3 – 1/6 = 1/6
Gaining ratio = 2:1
New Ratio = 2:1
Q6)-10 men working 8 hours a day can finish a work in 12 days. In how many days can 12 men working 5 hours a day finish the same work?
A7)-
This can be arranged as-

Then
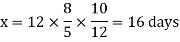
Q7)-Two numbers are in the ratio of 3: 5 and if 10 be subtracted from each of them, the remainders are in the ratio of 1: 5, find the numbers.
A8)-
Let the numbers be x and y, so that- x/y =3/5 or 5x = 3y … (1)
Again-
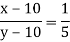
Or
5x – y = 40… (2)
By solving (1) and (2), we get-
X = 12 and y = 20
Hence the required numbers are- 12 and 20
Q8)- The prime cost of an article was three times the value of material used. The cost of raw materials was increased in the ratio 3: 4 and the productive wage was increased in the ratio 4: 5. Find the present prime cost of an article, which could formerly be made for Rs.180.
A9)-
Prime cost = x + y, where x = productive wage, y = material used
Now prime cost = 180 =3y or, y = 60, again x + y = 180, x = 180–y = 180–60 = 120
Present material cost = 4y/3 and present wage = 5x / 4
Present prime cost–

Hence the present prime cost is Rs. 230.
Q9)-A machine in a drinking water supplying factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
A10)-
Let the bottles filled by machine in 5 hours be x
We can write the given information as follows-
Number of bottles | Tine taken (in hrs) |
840 | 6 |
X | 5 |
There is a direct relationship between time taken and bottles filled by machine,
So that, we get-
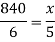
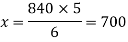
So that 700 bottles can be filled by the machine in 5 hrs.
Q10)-In a model of a ship, the mast is 9 m high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?
A11)-
Suppose the mast of the model ship be x, then
We can write the given information as follows-
| Height of mast | Length of ship |
Model ship | 9 m | x |
Actual ship | 12m | 28m |
There is a direct relationship-
So that,
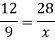
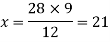
So that the length of a model ship is 21m.
Q11)-10 men can do a piece of work in 30 days then in how many days 20 men can do the same work?
A12)-
Let ‘x’ days be taken to do the task,
Then
Men | Days |
10 | 30 |
20 | X |
There is inverse relationship, so that-
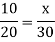
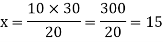
So that 20 men can do the same piece of work in 15 days.
Q12)-A person has a monthly salary of Rs. 20,000. He spends 8000 per month on food then what percent of his monthly salary does he save?
A13)-
Person’s monthly salary = 20,000
Savings = (20,000 – 8000) = 12,000
Fraction of his saving = 12,000/20,000
By converting the fraction into percentage, we get-
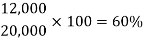
Q13)-A shopkeeper reduced the price of an item by 25%, the old price was 120 then find out the new price.
A14)-
25% of 120 will be-
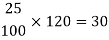
Which means he reduced Rs. 30, then the new price is-
120 – 30 = 90
The new price is Rs. 90
Q14)-If 20% of any number is 500 then find out the number?
A15)-
Let the number is ‘x’, then-
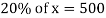


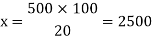
Hence the number is 2500.
Decrease in number = Original number – New number