Unit 2

Simultaneous Equations

Q1)-Discuss characteristics of simultaneous equations.

A1)-

1) A system of linear equations in one variable is not taken under simultaneous equations.

2) The set of values of two variables x and y which satisfy each equation in the system of equations is called the solution of simultaneous equations.

The solutions of two variable linear simultaneous equations may be –

i) Infinitely many,

Ii) A unique solution, or

Iii) No solution.

3) For simultaneous equations –

a1x + b1y = c1 and a2x + b2y = c2

a. If 𝑎1𝑎2=𝑏1𝑏2=𝑘 𝑎𝑛𝑑 𝑐1=𝑘 C2 then there are infinitely many solutions.

b. If 𝑎1𝑎2=𝑏1𝑏2=𝑐1 ≠ kc2, then there is no solution.

c. If c2 ≠ 0, then c1 = kc2  𝑐1𝑐2=𝑘, ℎ𝑒𝑛𝑐𝑒

𝑎1𝑎2=𝑏1𝑏2=𝑐1𝑐2→𝑖𝑛𝑓𝑖𝑛𝑖𝑡𝑒𝑙𝑦 𝑚𝑎𝑛𝑦 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑠 𝑎𝑛𝑑 𝑎1𝑎2=𝑏1𝑏2≠𝑐1𝑐2→𝑛𝑜 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛

d. If c1 and c2 both are zero (i.e., c1=0=c2)

Q2)- What are the different types of simultaneous equations?

A2)-

i) Linear Simultaneous Equations in two Variables – Two linear equations in two variables together are linear simultaneous equations in two variables, e.g.:

4x+y = 2

3x-5y = 18

Ii) Linear Simultaneous Equations in three Variables – Three linear equations in three variables together are linear simultaneous equations in three variables, e.g.:

3x+5y-7z = 13

4x+y-12z = 6

2x+9y-3z = 20

Iii) Specific type of Simultaneous Equations – The equations in other than linear form is called specific type equations, e.g.:

i)                   quadratic equation: ax2 + bx + c = 0

Ii)                 reciprocal equation: 𝑎𝑥+𝑏𝑦 =𝑐

Iii)              a 𝑦𝑥 + 𝑐=𝑏𝑦, 𝑒𝑡𝑐.

Q3)- Solve

          2x + 4y = 10
          2x + y = 4

A3)-

The coefficient of y in Equation 2 is 1. So first we make y the subject of Equation 2:

y = 4 - 2x

Next, substitute this expression for y in Equation 1 and solve for x:

Finally, substitute the solution for x into the expression for y:

y = 4 - 2(1) = 2
y = 2

So the solution to the pair of simultaneous linear equations is (1,2).
 

Q4) Solve

          x - 5y = 7
        2x -4y = 8

A4)-

The coefficient of x in Equation 1 is 1. So first we make x the subject of Equation 1:

x = 7 + 5y

Next, substitute this expression for x in Equation 2 and solve for y:

Finally, substitute the solution for y into the expression for x:

x = 7 + 5(-1) = 2
x = 2

So the solution to the pair of simultaneous linear equations is (2,-1).
 

Q5) Solve

         2x + 4y = 12
          x + 8y = 30

A5)-

The coefficient of x in Equation 2 is 1. So first we make x the subject of Equation 2:

x = 30 - 8y

Next, substitute this expression for x in Equation 1 and solve for y:

Finally, substitute the solution for y into the expression for x:

x = 30 - 8(4) = -2
x = -2

So the solution to the pair of simultaneous linear equations is (-2,2).
 

Q6) Solve:

         2x - 4y = 10
       -4x+5y = -26

A6)-

None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make x the subject of Equation 1:

x = (10 + 4y)/2
x = 5 + 2y

Next, substitute this expression for x in Equation 2 and solve for y:

-4(5 + 2y ) + 5y = -26
-20 - 8y + 5y = -26
-3y = -6
y = 2

Finally, substitute the solution for y into the expression for x:

x = 5 + 2(2) = 9
x = 9

So the solution to the pair of simultaneous linear equations is (9,2).
 

Q7)- Solve

            6x + 2y = 10
            10x - 3y = 12

A7)-

None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make y the subject of Equation 2:

y = (12-10x)/(-3)
y = -4 + (10/3) x

Next, substitute this expression for y in Equation 1 and solve for x:

6x + 2(-4 + (10/3) x) = 10
6x - 8 + (20/3) x = 10
(38/3) x = 18
x = 18*(3/38) = 27/19

Finally, substitute the solution for x into the expression for y:

y = -4 + (10/3)/(27/19) = -4 + 270/57 = -228/57 = 270/57 = 42/57 = 14/19

So the solution to the pair of simultaneous linear equations is (27/19,5/19)

Q8)- Solve the following simultaneous equations by using the elimination method:

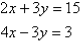
A8):

Label the equations as follows:

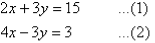
Notice that 3y appears on the left-hand side of both equations.  Adding the left-hand side of (1) and (2), and then the right-hand sides, gives:

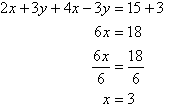
Note:

We have added equals to equals, and addition eliminates y.

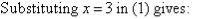
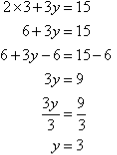
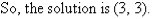
Q9)- Solve the following simultaneous equations by using the elimination method:

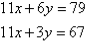
A9):

Label the equations as follows:

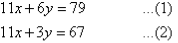
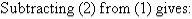
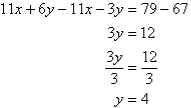
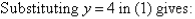
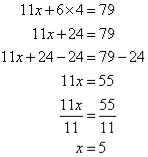
So, the solution is (5, 4)
 

Q10: Solve the following simultaneous equations by using the elimination method:

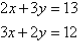
A10):

Label the equations as follows:

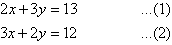
Multiplying (1) by 2 and (2) by 3 gives:

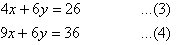
Subtracting (3) from (4) gives:

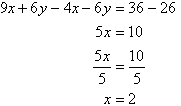
So, the solution is (2, 3).

Q10)- Solve the following simultaneous equations by using the elimination method:

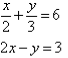
A11):

Label the equations as follows:

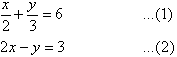
To simplify equation (1), multiply both sides by 6, the lowest common denominator of 2 and 3.

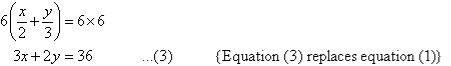
The equations are now:

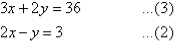
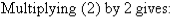
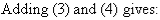
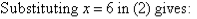
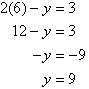
So, the solution is (6, 9).

Unit 2

Unit 2

Unit 2

Simultaneous Equations

Q1)-Discuss characteristics of simultaneous equations.

A1)-

1) A system of linear equations in one variable is not taken under simultaneous equations.

2) The set of values of two variables x and y which satisfy each equation in the system of equations is called the solution of simultaneous equations.

The solutions of two variable linear simultaneous equations may be –

i) Infinitely many,

Ii) A unique solution, or

Iii) No solution.

3) For simultaneous equations –

a1x + b1y = c1 and a2x + b2y = c2

a. If 𝑎1𝑎2=𝑏1𝑏2=𝑘 𝑎𝑛𝑑 𝑐1=𝑘 C2 then there are infinitely many solutions.

b. If 𝑎1𝑎2=𝑏1𝑏2=𝑐1 ≠ kc2, then there is no solution.

c. If c2 ≠ 0, then c1 = kc2  𝑐1𝑐2=𝑘, ℎ𝑒𝑛𝑐𝑒

𝑎1𝑎2=𝑏1𝑏2=𝑐1𝑐2→𝑖𝑛𝑓𝑖𝑛𝑖𝑡𝑒𝑙𝑦 𝑚𝑎𝑛𝑦 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑠 𝑎𝑛𝑑 𝑎1𝑎2=𝑏1𝑏2≠𝑐1𝑐2→𝑛𝑜 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛

d. If c1 and c2 both are zero (i.e., c1=0=c2)

Q2)- What are the different types of simultaneous equations?

A2)-

i) Linear Simultaneous Equations in two Variables – Two linear equations in two variables together are linear simultaneous equations in two variables, e.g.:

4x+y = 2

3x-5y = 18

Ii) Linear Simultaneous Equations in three Variables – Three linear equations in three variables together are linear simultaneous equations in three variables, e.g.:

3x+5y-7z = 13

4x+y-12z = 6

2x+9y-3z = 20

Iii) Specific type of Simultaneous Equations – The equations in other than linear form is called specific type equations, e.g.:

i)                   quadratic equation: ax2 + bx + c = 0

Ii)                 reciprocal equation: 𝑎𝑥+𝑏𝑦 =𝑐

Iii)              a 𝑦𝑥 + 𝑐=𝑏𝑦, 𝑒𝑡𝑐.

Q3)- Solve

          2x + 4y = 10
          2x + y = 4

A3)-

The coefficient of y in Equation 2 is 1. So first we make y the subject of Equation 2:

y = 4 - 2x

Next, substitute this expression for y in Equation 1 and solve for x:

Finally, substitute the solution for x into the expression for y:

y = 4 - 2(1) = 2
y = 2

So the solution to the pair of simultaneous linear equations is (1,2).
 

Q4) Solve

          x - 5y = 7
        2x -4y = 8

A4)-

The coefficient of x in Equation 1 is 1. So first we make x the subject of Equation 1:

x = 7 + 5y

Next, substitute this expression for x in Equation 2 and solve for y:

Finally, substitute the solution for y into the expression for x:

x = 7 + 5(-1) = 2
x = 2

So the solution to the pair of simultaneous linear equations is (2,-1).
 

Q5) Solve

         2x + 4y = 12
          x + 8y = 30

A5)-

The coefficient of x in Equation 2 is 1. So first we make x the subject of Equation 2:

x = 30 - 8y

Next, substitute this expression for x in Equation 1 and solve for y:

Finally, substitute the solution for y into the expression for x:

x = 30 - 8(4) = -2
x = -2

So the solution to the pair of simultaneous linear equations is (-2,2).
 

Q6) Solve:

         2x - 4y = 10
       -4x+5y = -26

A6)-

None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make x the subject of Equation 1:

x = (10 + 4y)/2
x = 5 + 2y

Next, substitute this expression for x in Equation 2 and solve for y:

-4(5 + 2y ) + 5y = -26
-20 - 8y + 5y = -26
-3y = -6
y = 2

Finally, substitute the solution for y into the expression for x:

x = 5 + 2(2) = 9
x = 9

So the solution to the pair of simultaneous linear equations is (9,2).
 

Q7)- Solve

            6x + 2y = 10
            10x - 3y = 12

A7)-

None of the coefficients are 1. So we can choose to make any variable the subject.
Let’s make y the subject of Equation 2:

y = (12-10x)/(-3)
y = -4 + (10/3) x

Next, substitute this expression for y in Equation 1 and solve for x:

6x + 2(-4 + (10/3) x) = 10
6x - 8 + (20/3) x = 10
(38/3) x = 18
x = 18*(3/38) = 27/19

Finally, substitute the solution for x into the expression for y:

y = -4 + (10/3)/(27/19) = -4 + 270/57 = -228/57 = 270/57 = 42/57 = 14/19

So the solution to the pair of simultaneous linear equations is (27/19,5/19)

Q8)- Solve the following simultaneous equations by using the elimination method:

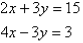
A8):

Label the equations as follows:

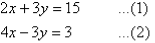
Notice that 3y appears on the left-hand side of both equations.  Adding the left-hand side of (1) and (2), and then the right-hand sides, gives:

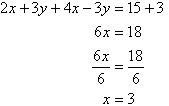
Note:

We have added equals to equals, and addition eliminates y.

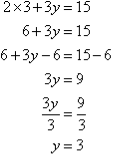
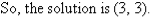
Q9)- Solve the following simultaneous equations by using the elimination method:

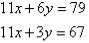
A9):

Label the equations as follows:

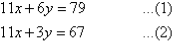
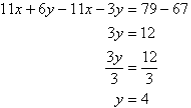
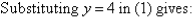
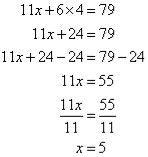
So, the solution is (5, 4)
 

Q10: Solve the following simultaneous equations by using the elimination method:

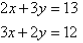
A10):

Label the equations as follows:

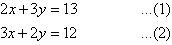
Multiplying (1) by 2 and (2) by 3 gives:

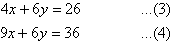
Subtracting (3) from (4) gives:

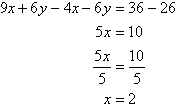
So, the solution is (2, 3).

Q10)- Solve the following simultaneous equations by using the elimination method:

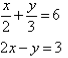
A11):

Label the equations as follows:

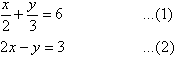
To simplify equation (1), multiply both sides by 6, the lowest common denominator of 2 and 3.

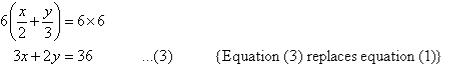
The equations are now:

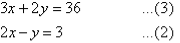
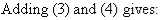
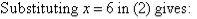
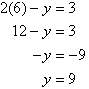
So, the solution is (6, 9).