Unit 3

Elementary Matrices

Q1)- Express the matrix A as sum of hermitian and skew-hermitian matrix where

A1)-

Let A =

Therefore 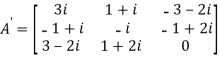   and

        Let

Again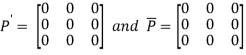

Hence P is a hermitian matrix.

Let 

Again

Hence Q is a skew- hermitian matrix.

We Check

  P +Q=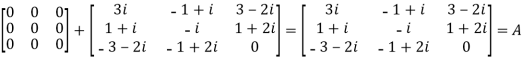

Hence proved.

Q2)- If A = 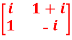  then show that

(i) is hermitian matrix.

(ii) 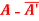  is  skew-hermitian matrix.

A2)-

Given   A =

Then 

Let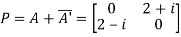

Also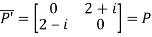  

Hence P is a Hermitian matrix.

Let

Also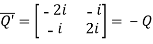

Hence Q is a   skew-hermitian matrix.

Q3)- Check whether the following matrix A is symmetric or not?

                                            A =

A3)-

This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A.

                                       -A = A’

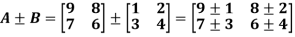
Q4)- Add .

A4)-

A + B =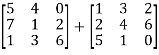

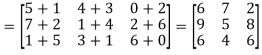
Q5)-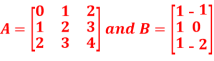

A5)-

Then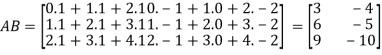

Q6)- Discuss Skew Hermitian Matrix.

A6)-

Skew-Hermitian matrix-

A square matrix A = 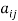is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.

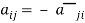
Note- all the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.

For example:

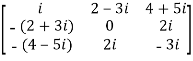
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-

                                            - A = (͞A)’

Note:   A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.

Similarly a Skew- Hermitian matrix is a generalization of a  Skew symmetric matrix  and also every Skew- symmetric matrix  is Skew –Hermitian.

Theorem: Every square complex   matrix   can   be uniquely   expressed as sum hermitian and skew-hermitian matrix.

Or If A   is given square complex matrix then 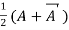 is   hermitian and  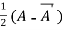is skew-hermitian matrices.

Q7)- Discuss different types of matrices.

A7)-

Types of matrices-

1. Rectangular matrix-

A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.

Example:

                                     A =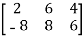

The order of matrix A is 2×3 , that means it has two rows and three columns.

Matrix A is a rectangular matrix.

2. Square matrix-

A matrix which has equal number of rows and columns, is called square matrix.

Example:

A =

The order of matrix A is 3 ×3 , that means it has three rows and three columns.

Matrix A is a square matrix.

3. Row matrix-

A matrix with a single row and any number of columns is called row matrix.

Example:

A =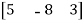

4. Column matrix-

A matrix with a single column and any number of rows is called row matrix.

Example:

A =

5. Null matrix (Zero matrix)-

A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by O

Example:

A =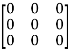

6. Diagonal matrix-

A matrix is said to be diagonal matrix if all the elements except principal diagonal are zero

The diagonal matrix always follows-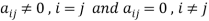

Example:

A =

7. Scalar matrix-

A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.

Example-

A =

8. Identity matrix-

A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.

It is denoted by – ‘I’

I =

9. Triangular matrix-

If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.

There are two types of triangular matrices-

(a) Lower triangular matrix-

If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.

Example:

                                             A =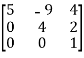

(b) Upper triangular matrix-

If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.

Example-

                                                      A =

Unit 3

Unit 3

Unit 3

Elementary Matrices

Q1)- Express the matrix A as sum of hermitian and skew-hermitian matrix where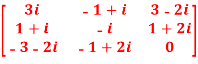

A1)-

Let A =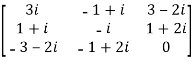

Therefore 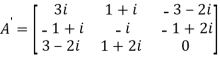   and

        Let

Again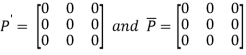

Hence P is a hermitian matrix.

Let 

Again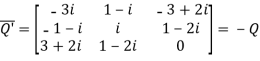

Hence Q is a skew- hermitian matrix.

We Check

  P +Q=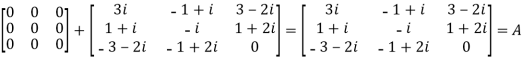

Hence proved.

Q2)- If A = 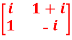  then show that

(i) is hermitian matrix.

(ii) 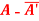  is  skew-hermitian matrix.

A2)-

Given   A =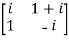

Then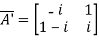 

Let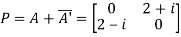

Also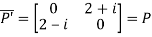  

Hence P is a Hermitian matrix.

Let

Also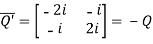

Hence Q is a   skew-hermitian matrix.

Q3)- Check whether the following matrix A is symmetric or not?

                                            A =

A3)-

This is not a skew symmetric matrix, because the transpose of matrix A is not equals to -A.

                                       -A = A’

Q4)- Add .

A4)-

A + B =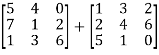

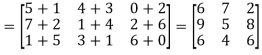
Q5)-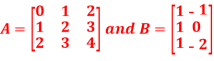

A5)-

Then

Q6)- Discuss Skew Hermitian Matrix.

A6)-

Skew-Hermitian matrix-

A square matrix A = 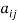is said to be hermitian matrix if every element of A is equal to negative conjugate complex j-ith element of A.

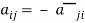
Note- all the diagonal elements of a skew hermitian matrix are either zero or pure imaginary.

For example:

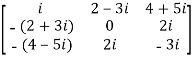
The necessary and sufficient condition for a matrix A to be skew hermitian will be as follows-

                                            - A = (͞A)’

Note:   A Hermitian matrix is a generalization of a real symmetric matrix and also every real symmetric matrix is Hermitian.

Similarly a Skew- Hermitian matrix is a generalization of a  Skew symmetric matrix  and also every Skew- symmetric matrix  is Skew –Hermitian.

Theorem: Every square complex   matrix   can   be uniquely   expressed as sum hermitian and skew-hermitian matrix.

Or If A   is given square complex matrix then 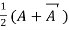 is   hermitian and  is skew-hermitian matrices.

Q7)- Discuss different types of matrices.

A7)-

Types of matrices-

1. Rectangular matrix-

A matrix in which the number of rows is not equal to the number of columns, are called rectangular matrix.

Example:

                                     A =

The order of matrix A is 2×3 , that means it has two rows and three columns.

Matrix A is a rectangular matrix.

2. Square matrix-

A matrix which has equal number of rows and columns, is called square matrix.

Example:

A =

The order of matrix A is 3 ×3 , that means it has three rows and three columns.

Matrix A is a square matrix.

3. Row matrix-

A matrix with a single row and any number of columns is called row matrix.

Example:

A =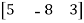

4. Column matrix-

A matrix with a single column and any number of rows is called row matrix.

Example:

A =

5. Null matrix (Zero matrix)-

A matrix in which each element is zero, then it is called null matrix or zero matrix and denoted by O

Example:

A =

6. Diagonal matrix-

A matrix is said to be diagonal matrix if all the elements except principal diagonal are zero

The diagonal matrix always follows-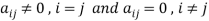

Example:

A =

7. Scalar matrix-

A diagonal matrix in which all the diagonal elements are equal to a scalar, is called scalar matrix.

Example-

A =

8. Identity matrix-

A diagonal matrix is said to be an identity matrix if its each element of diagonal is unity or 1.

It is denoted by – ‘I’

I =

9. Triangular matrix-

If every element above or below the leading diagonal of a square matrix is zero, then the matrix is known as a triangular matrix.

There are two types of triangular matrices-

(a) Lower triangular matrix-

If all the elements below the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.

Example:

                                             A =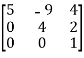

(b) Upper triangular matrix-

If all the elements above the leading diagonal of a square matrix are zero, then it is called lower triangular matrix.

Example-

                                                      A =