Unit 4
Logarithm and Anti-logarithm
Q1)- Explain Logarithm.
A1)-
A logarithm is the power to which a number must be raised in order to get some other number. For example, the base ten logarithm of 100 is 2, because ten raised to the power of two is 100:
Log 100 = 2
Because
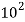 = 100
= 100
This is an example of a base-ten logarithm. We call it a base ten logarithm because ten is the number that is raised to a power. The base unit is the number being raised to a power. There are logarithms using different base units. If you wanted, you could use two as a base unit. For instance, the base two logarithm of eight is three, because two raised to the power of three equals eight:
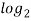 8 = 3
8 = 3
Because
 = 8
= 8
In general, you write log followed by the base number as a subscript. The most common logarithms are base 10 logarithms and natural logarithms; they have special notations. A base ten log is written
Log
And a base ten logarithmic equation is usually written in the form:
Log a = r
A natural logarithm is written
Ln
And a natural logarithmic equation is usually written in the form:
Ln a = r
So, when you see log by itself, it means base ten log. When you see ln, it means natural logarithm (we'll define natural logarithms below). In this course only base ten and natural logarithms will be used.
Q2)- What are the properties of logarithm?
A2)-
Properties of Logarithms
-
 mn =
mn = 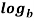 m +
m + 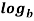 n
n 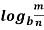 =
=  m -
m -  n
n = p
= p 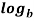 n
n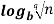 =
= 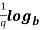 n
n n =
n =  n
n  a
a- Zero Exponent Rule:
 1 = 0
1 = 0
Q3)- Express 53 = 125 in logarithm form.
A3)-
53 = 125
As we know,
ab = c ⇒ logac=b
Therefore;
Log5125 = 3
Q4)-Express log101 = 0 in exponential form.
A4)-
Given, log101 = 0
By the rule, we know;
Logac=b ⇒ ab = c
Hence,
100 = 1
Q5)-Find the log of 32 to the base 4.
A5)-
Log432 = x
4x = 32
(22)x = 2x2x2x2x2
22x = 25
2x=5
x=5/2
Therefore,
Log432 =5/2
Q6)- Find x if log5(x-7) =1.
A6)-
Given,
Log5(x-7) =1
Using logarithm rules, we can write;
51 = x-7
5 = x-7
x=5+7
x=12
Q7)- If logam=n, express an-1 in terms of a and m.
A7)-
Logam=n
an=m
an/a=m/a
an-1=m/a
6.
Q8)- Solve for x if log(x-1) +log(x+1) =log21
A8)-
Log(x-1) +log(x+1) =log21
Log(x-1) +log(x+1) =0
Log[(x-1) (x+1)] =0
Since, log 1 = 0
(x-1) (x+1) = 1
x2-1=1
x2=2
x=± √2
Since, log of negative number is not defined.
Therefore, x=√2
Q9)- Express log (75/16)-2log (5/9) +log (32/243) in terms of log 2 and log 3.
A9)-
Log (75/16)-2log (5/9) +log (32/243)
Since, nlogam=logamn
⇒log (75/16)-log (5/9)2+log (32/243)
⇒log (75/16)-log (25/81) +log (32/243)
Since, logam-logan=loga(m/n)
⇒log [(75/16) ÷ (25/81)] +log (32/243)
⇒log [(75/16) × (81/25)] +log (32/243)
⇒log (243/16) +log (32/243)
Since, logam+logan=logamn
⇒log (32/16)
⇒log2
Q10)-Express 2logx+3logy=log a in logarithm free form.
A10)-
2logx+3logy=log a
Logx2+logy3=log a
Logx2y3=log a
x2y3=log a
Q11)-Prove that: 2log (15/18)-log (25/162) +log (4/9) =log2
A11)-
2log (15/18)-log (25/162) +log (4/9) =log2
Taking L.H.S.:
⇒2log (15/18)-log (25/162) +log (4/9)
⇒log (15/18)2-log (25/162) +log (4/9)
⇒log (225/324)-log (25/162) +log (4/9)
⇒log [(225/324) (4/9)]-log (25/162)
⇒log [(225/324) (4/9)]/ (25/162)
⇒log (72/36)
⇒log2 (R.H.S)
Q12)-Express log10(2+1) in the form of log10x.
A12)-
log10(2+1)
=log102+log101
=log10(2×10)
=log1020
Q13)- Find the value of x, if log10(x-10) =1.
A13)-
Given, log10(x-10) =1.
Log10(x-10) = log1010
x-10 = 10
x=10+10
x=20
Q14)-If log x = -2.0258, find x.
A14)-
In order to find the value of x using antilog-table, the decimal part (i.e., the mantissa) must be made positive. For this we proceed as follows:
log x = -2.0258 = - 3 + 3 - 2.0258
= - 3 + .9742 =3.9742
Therefore, x = antilog 3.9742.
Now, from antilog table we get the number corresponding to the mantissa
.9742 as (9419 + 4) = 9423.
Again the characteristic in log x is (- 3).
Hence, there should be two zeroes between the decimal point and the first significant digit in the value of x.
Therefore, x = .009423.
Unit 4
Logarithm and Anti-logarithm
Q1)- Explain Logarithm.
A1)-
A logarithm is the power to which a number must be raised in order to get some other number. For example, the base ten logarithm of 100 is 2, because ten raised to the power of two is 100:
Log 100 = 2
Because
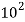 = 100
= 100
This is an example of a base-ten logarithm. We call it a base ten logarithm because ten is the number that is raised to a power. The base unit is the number being raised to a power. There are logarithms using different base units. If you wanted, you could use two as a base unit. For instance, the base two logarithm of eight is three, because two raised to the power of three equals eight:
 8 = 3
8 = 3
Because
 = 8
= 8
In general, you write log followed by the base number as a subscript. The most common logarithms are base 10 logarithms and natural logarithms; they have special notations. A base ten log is written
Log
And a base ten logarithmic equation is usually written in the form:
Log a = r
A natural logarithm is written
Ln
And a natural logarithmic equation is usually written in the form:
Ln a = r
So, when you see log by itself, it means base ten log. When you see ln, it means natural logarithm (we'll define natural logarithms below). In this course only base ten and natural logarithms will be used.
Q2)- What are the properties of logarithm?
A2)-
Properties of Logarithms
-
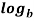 mn =
mn = 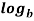 m +
m +  n
n 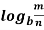 =
=  m -
m - 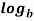 n
n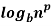 = p
= p 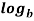 n
n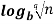 =
= 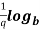 n
n n =
n = 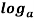 n
n 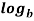 a
a- Zero Exponent Rule:
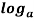 1 = 0
1 = 0
Q3)- Express 53 = 125 in logarithm form.
A3)-
53 = 125
As we know,
ab = c ⇒ logac=b
Therefore;
Log5125 = 3
Q4)-Express log101 = 0 in exponential form.
A4)-
Given, log101 = 0
By the rule, we know;
Logac=b ⇒ ab = c
Hence,
100 = 1
Q5)-Find the log of 32 to the base 4.
A5)-
Log432 = x
4x = 32
(22)x = 2x2x2x2x2
22x = 25
2x=5
x=5/2
Therefore,
Log432 =5/2
Q6)- Find x if log5(x-7) =1.
A6)-
Given,
Log5(x-7) =1
Using logarithm rules, we can write;
51 = x-7
5 = x-7
x=5+7
x=12
Q7)- If logam=n, express an-1 in terms of a and m.
A7)-
Logam=n
an=m
an/a=m/a
an-1=m/a
6.
Q8)- Solve for x if log(x-1) +log(x+1) =log21
A8)-
Log(x-1) +log(x+1) =log21
Log(x-1) +log(x+1) =0
Log[(x-1) (x+1)] =0
Since, log 1 = 0
(x-1) (x+1) = 1
x2-1=1
x2=2
x=± √2
Since, log of negative number is not defined.
Therefore, x=√2
Q9)- Express log (75/16)-2log (5/9) +log (32/243) in terms of log 2 and log 3.
A9)-
Log (75/16)-2log (5/9) +log (32/243)
Since, nlogam=logamn
⇒log (75/16)-log (5/9)2+log (32/243)
⇒log (75/16)-log (25/81) +log (32/243)
Since, logam-logan=loga(m/n)
⇒log [(75/16) ÷ (25/81)] +log (32/243)
⇒log [(75/16) × (81/25)] +log (32/243)
⇒log (243/16) +log (32/243)
Since, logam+logan=logamn
⇒log (32/16)
⇒log2
Q10)-Express 2logx+3logy=log a in logarithm free form.
A10)-
2logx+3logy=log a
Logx2+logy3=log a
Logx2y3=log a
x2y3=log a
Q11)-Prove that: 2log (15/18)-log (25/162) +log (4/9) =log2
A11)-
2log (15/18)-log (25/162) +log (4/9) =log2
Taking L.H.S.:
⇒2log (15/18)-log (25/162) +log (4/9)
⇒log (15/18)2-log (25/162) +log (4/9)
⇒log (225/324)-log (25/162) +log (4/9)
⇒log [(225/324) (4/9)]-log (25/162)
⇒log [(225/324) (4/9)]/ (25/162)
⇒log (72/36)
⇒log2 (R.H.S)
Q12)-Express log10(2+1) in the form of log10x.
A12)-
log10(2+1)
=log102+log101
=log10(2×10)
=log1020
Q13)- Find the value of x, if log10(x-10) =1.
A13)-
Given, log10(x-10) =1.
Log10(x-10) = log1010
x-10 = 10
x=10+10
x=20
Q14)-If log x = -2.0258, find x.
A14)-
In order to find the value of x using antilog-table, the decimal part (i.e., the mantissa) must be made positive. For this we proceed as follows:
log x = -2.0258 = - 3 + 3 - 2.0258
= - 3 + .9742 =3.9742
Therefore, x = antilog 3.9742.
Now, from antilog table we get the number corresponding to the mantissa
.9742 as (9419 + 4) = 9423.
Again the characteristic in log x is (- 3).
Hence, there should be two zeroes between the decimal point and the first significant digit in the value of x.
Therefore, x = .009423.
Unit 4
Logarithm and Anti-logarithm
Q1)- Explain Logarithm.
A1)-
A logarithm is the power to which a number must be raised in order to get some other number. For example, the base ten logarithm of 100 is 2, because ten raised to the power of two is 100:
Log 100 = 2
Because
 = 100
= 100
This is an example of a base-ten logarithm. We call it a base ten logarithm because ten is the number that is raised to a power. The base unit is the number being raised to a power. There are logarithms using different base units. If you wanted, you could use two as a base unit. For instance, the base two logarithm of eight is three, because two raised to the power of three equals eight:
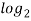 8 = 3
8 = 3
Because
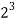 = 8
= 8
In general, you write log followed by the base number as a subscript. The most common logarithms are base 10 logarithms and natural logarithms; they have special notations. A base ten log is written
Log
And a base ten logarithmic equation is usually written in the form:
Log a = r
A natural logarithm is written
Ln
And a natural logarithmic equation is usually written in the form:
Ln a = r
So, when you see log by itself, it means base ten log. When you see ln, it means natural logarithm (we'll define natural logarithms below). In this course only base ten and natural logarithms will be used.
Q2)- What are the properties of logarithm?
A2)-
Properties of Logarithms
-
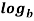 mn =
mn =  m +
m + 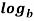 n
n 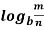 =
=  m -
m - 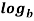 n
n = p
= p  n
n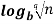 =
= 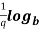 n
n n =
n = 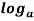 n
n 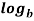 a
a- Zero Exponent Rule:
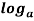 1 = 0
1 = 0
Q3)- Express 53 = 125 in logarithm form.
A3)-
53 = 125
As we know,
ab = c ⇒ logac=b
Therefore;
Log5125 = 3
Q4)-Express log101 = 0 in exponential form.
A4)-
Given, log101 = 0
By the rule, we know;
Logac=b ⇒ ab = c
Hence,
100 = 1
Q5)-Find the log of 32 to the base 4.
A5)-
Log432 = x
4x = 32
(22)x = 2x2x2x2x2
22x = 25
2x=5
x=5/2
Therefore,
Log432 =5/2
Q6)- Find x if log5(x-7) =1.
A6)-
Given,
Log5(x-7) =1
Using logarithm rules, we can write;
51 = x-7
5 = x-7
x=5+7
x=12
Q7)- If logam=n, express an-1 in terms of a and m.
A7)-
Logam=n
an=m
an/a=m/a
an-1=m/a
6.
Q8)- Solve for x if log(x-1) +log(x+1) =log21
A8)-
Log(x-1) +log(x+1) =log21
Log(x-1) +log(x+1) =0
Log[(x-1) (x+1)] =0
Since, log 1 = 0
(x-1) (x+1) = 1
x2-1=1
x2=2
x=± √2
Since, log of negative number is not defined.
Therefore, x=√2
Q9)- Express log (75/16)-2log (5/9) +log (32/243) in terms of log 2 and log 3.
A9)-
Log (75/16)-2log (5/9) +log (32/243)
Since, nlogam=logamn
⇒log (75/16)-log (5/9)2+log (32/243)
⇒log (75/16)-log (25/81) +log (32/243)
Since, logam-logan=loga(m/n)
⇒log [(75/16) ÷ (25/81)] +log (32/243)
⇒log [(75/16) × (81/25)] +log (32/243)
⇒log (243/16) +log (32/243)
Since, logam+logan=logamn
⇒log (32/16)
⇒log2
Q10)-Express 2logx+3logy=log a in logarithm free form.
A10)-
2logx+3logy=log a
Logx2+logy3=log a
Logx2y3=log a
x2y3=log a
Q11)-Prove that: 2log (15/18)-log (25/162) +log (4/9) =log2
A11)-
2log (15/18)-log (25/162) +log (4/9) =log2
Taking L.H.S.:
⇒2log (15/18)-log (25/162) +log (4/9)
⇒log (15/18)2-log (25/162) +log (4/9)
⇒log (225/324)-log (25/162) +log (4/9)
⇒log [(225/324) (4/9)]-log (25/162)
⇒log [(225/324) (4/9)]/ (25/162)
⇒log (72/36)
⇒log2 (R.H.S)
Q12)-Express log10(2+1) in the form of log10x.
A12)-
log10(2+1)
=log102+log101
=log10(2×10)
=log1020
Q13)- Find the value of x, if log10(x-10) =1.
A13)-
Given, log10(x-10) =1.
Log10(x-10) = log1010
x-10 = 10
x=10+10
x=20
Q14)-If log x = -2.0258, find x.
A14)-
In order to find the value of x using antilog-table, the decimal part (i.e., the mantissa) must be made positive. For this we proceed as follows:
log x = -2.0258 = - 3 + 3 - 2.0258
= - 3 + .9742 =3.9742
Therefore, x = antilog 3.9742.
Now, from antilog table we get the number corresponding to the mantissa
.9742 as (9419 + 4) = 9423.
Again the characteristic in log x is (- 3).
Hence, there should be two zeroes between the decimal point and the first significant digit in the value of x.
Therefore, x = .009423.