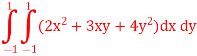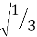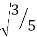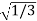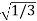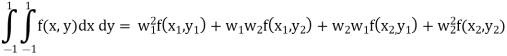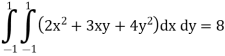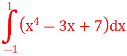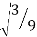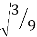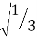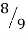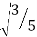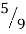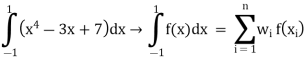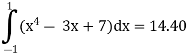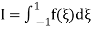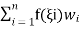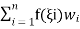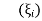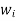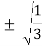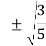|
|
|
|
|
|
|
|
Step 1- To find the point of gaussian Quadrature 2n-1 = Higher order = 2 n= 1.5 n~2 (Two point Quadrature problem) Step 2 - To find gaussian location and weights
Since it is double unequal, we have to take both x & y. x1 = + x2 = -
Step 3 All f(x) values here, substitute values of x1, x2, y1 & y2 F(x, y) = (2x2 + 3xy + 4y2) F(x1, y1) = (2x1 2 + 3x1y1 + 4y12) = 3 F(x1, y2) = (2x1 2 + 3x1y2 + 4y22) = 1 F(x2, y1) = (2x2 2 + 3x2y1 + 4y12) = 1 F(x2, y2) = (2x2 2 + 3x2y2 + 4y22) = 3 Step 4 Evaluate using double integral formula
Substitute w1, w2 and all f(x) values in above equation = (1×1×3)+(1×1×1)+(1×1×1)+(1×1×3)
|
|
 A8)
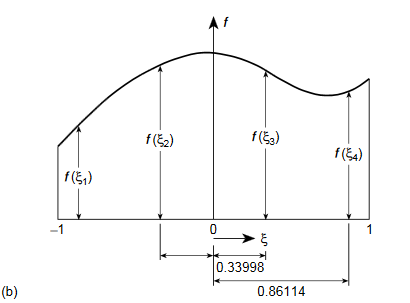
A8)Step 1 To find the point of Gaussian Quadrature 2n-1 = Higher order From given equation, Higher order = 4 2n-1 = 4 N=2.5 N~3 (Three point Quadrature problem) Step 2 To find qaussian location and weights
Step 3 Find Au f(x) values F(x)’(x4 – 3x + 7) dx F(x1) = x14 – 3x1 + 7 = 7 F(x2) = x24 – 3(x2 )+ 7 = 5.0362 F(x3) = x34 – 3(x3 )+ 7 = 9.6837 Step 4 Evaluate using single integral formula
→ w2 f(x1) + w2 f(x2) +w3 f(x3) = (0.8888 × 7) + (0.5555 × 5.0362) + (0.5555 × 9.6837)
|
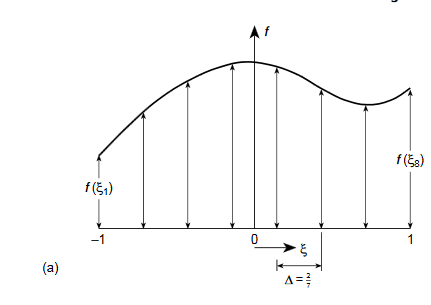
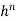 ) where his the element size. The well-known Newton–Cotes ‘quadrature ‘formulae can be written as
) where his the element size. The well-known Newton–Cotes ‘quadrature ‘formulae can be written as
|
|
|
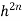 ).
).
|
Number of points ,n | Points | Weights |
1 | 0 | 2 |
2 |
|
1 |
3 |
0 |
|
|
|