Unit-1
Error and roots of Algebraic and Transcendental Equations
Q1) Describe some commonly used symbols in flow chart.
A1)
The commonly used symbols in a flow chart-
1.Terminal point
2. Input / Output-

3. Decision logic-
4. Processing operation box-

5. Connector point-
Q2) Define mean value theorem for derivatives.
A2) Mean value theorem for derivatives-
Suppose that f(x) be a function of x such that,
1. if it is continuous in [a, b]
2. if it is differentiable in (a, b)
Then there at least exists a value cϵ (a, b)
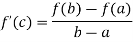
Q3) What do you understand by truncation error.
A3) The truncation errors are caused by approximated values or on replacing the infinite process to a finite value.
Example: 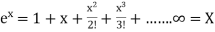 is replaced by
is replaced by 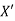 .
.
Then truncation error is 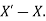
Q4) An approximate value of  is given by
is given by  and its exact value is
and its exact value is  Find the absolute and relative errors.
Find the absolute and relative errors.
A4) The absolute error is 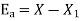
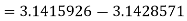
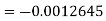 .
.
The relative error is
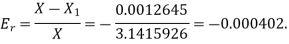
Q5) Find the difference  to three significant figures?
to three significant figures?
A5)
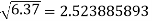
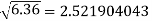
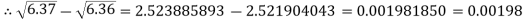
Correct to three decimal places.
Q6) Find the absolute error if the number  is truncate to three decimal places?
is truncate to three decimal places?
A6) The given number is 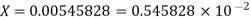
After truncate it to three decimal places the rounded value is 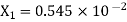
Therefore, the absolute error is 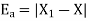
= 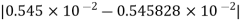
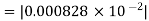
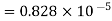 .
.
Q7) Find a real root of 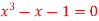 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
A7) Let 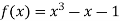 then by hit and trial we have
then by hit and trial we have
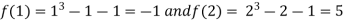
Thus 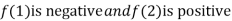 .So the root of the given equation should lie between 1 and 2.
.So the root of the given equation should lie between 1 and 2.

Now, 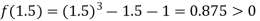
I.e., positive so the root of the given equation must lie between 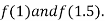

Now, 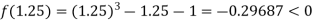
I.e., negative so the root of the given equation lies between 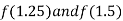
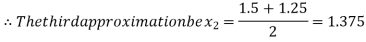
Now, 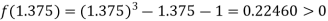
i.e., positive so the root of the given equation lies between 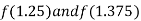
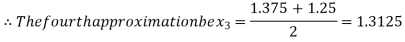
Now, 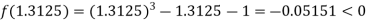
i.e., negative so that the root of the given equation lies between 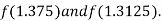
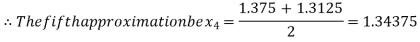
Now, 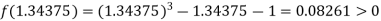
i.e., positive so that the root of the given equation lies between 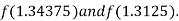
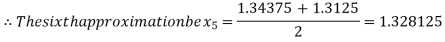
Now, 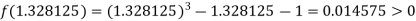
i.e., positive so that the root of the given equation lies between 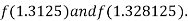
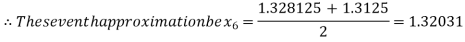
Now, 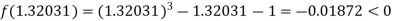
I.e., negative so that the root of the given equation lies between 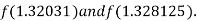
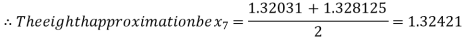
Now, 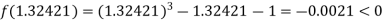
i.e., negative so that the root of the given equation lies between 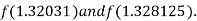
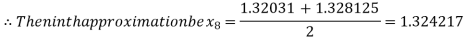
Hence the approximate root of the given equation is 1.32421
Q8) Find the root of the equation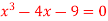 , using the bisection method.
, using the bisection method.
A8) Let 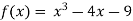 then by hit and trial we have
then by hit and trial we have
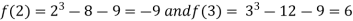
Thus 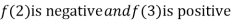 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 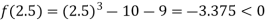
i.e., negative so the root of the given equation must lie between 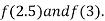

Now, 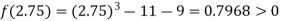
i.e., positive so the root of the given equation must lie between 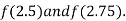
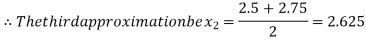
Now, 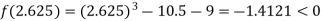
i.e., negative so the root of the given equation must lie between 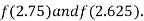
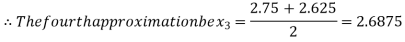
Now, 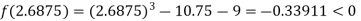
i.e., negative so the root of the given equation must lie between 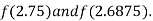
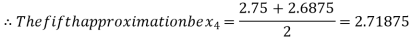
Now, 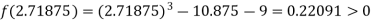
i.e., positive so the root of the given equation must lie between 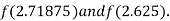
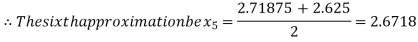
Now, 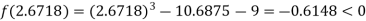
i.e., negative so the root of the given equation must lie between 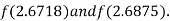
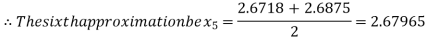
Hence the root of the given equation correct to two decimal place is 2.67965.
Q9) Find the root of the equation 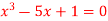 between 2 and 3, using bisection method correct to two decimal places.
between 2 and 3, using bisection method correct to two decimal places.
A9) Let 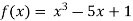
Where 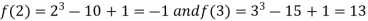
Thus 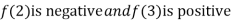 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 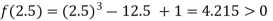
i.e., positive so the root of the given equation must lie between 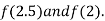

Now, 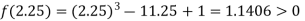
i.e., positive so the root of the given equation must lie between 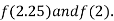
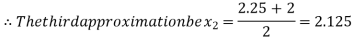
Now, 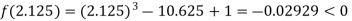
i.e., negative so the root of the given equation must lie between 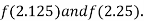
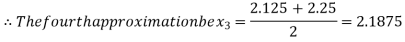
Now, 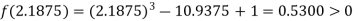
i.e., positive so the root of the given equation must lie between 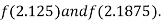
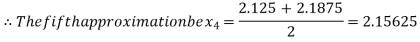
Now, 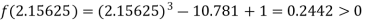
i.e., positive so the root of the given equation must lie between 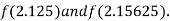
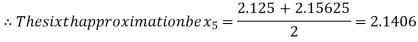
Now, 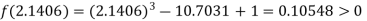
i.e., positive so the root of the given equation must lie between 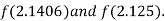
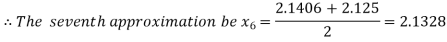
Now, 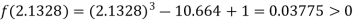
i.e., positive so the root of the given equation must lie between 
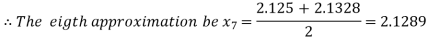
Now, 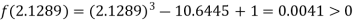
i.e., positive so the root of the given equation must lie between 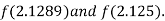
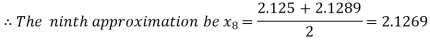
Hence the root of the given equation correct to two decimal place is 2.1269
Q10) Find the real root of the equation cos x = 3x – 1 correct to three decimal points by using iteration method.
A10) Here we have-
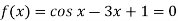
Now,
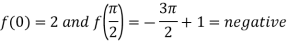
A root lies between 0 and  .
.
We can rewrite the equation as-
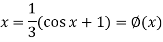
We have-
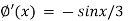
And
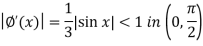
Here we can apply iteration method, starting with
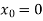
Then the successive approximation is-
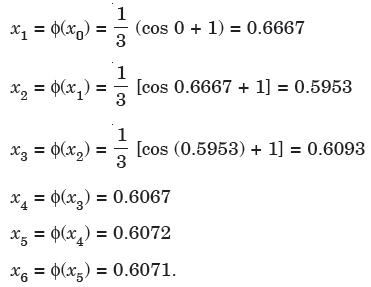
Here last two approximations are almost same, the root is 0.607 correct to 3 decimal places.
Q11) Starting with x = 0.12, solve x = 0.21 sin (0.5 + x) by using the iteration method.
A11) Here
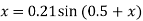
First approximation of x is gives as-
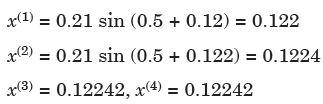
Here last two approx. are same, hence required root is 0.12242.
Q12) Define the method of false position (Regula- Falsi method)
A12) This is the oldest method of finding the approximate numerical value of a real root of an equation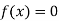 .
.
In this method we suppose that 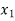 and
and 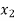 are two points where
are two points where 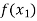 and
and 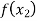 are of opposite sign. Let
are of opposite sign. Let 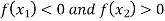
Hence the root of the equation 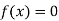 lies between
lies between 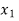 and
and 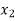 and so,
and so, 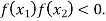
The Regula Falsi formula
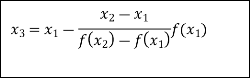
Find 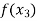 is positive or negative. If
is positive or negative. If 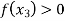 then root lies between
then root lies between 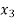 and
and 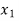 or if
or if 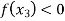 then root lies between
then root lies between 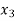 and
and 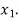 similarly we calculate
similarly we calculate 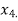
Proceed in this manner until the desired accurate root is found.
Q13) Find a real root of the equation  near
near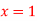 , correct to three decimal places by the Regula Falsi method.
, correct to three decimal places by the Regula Falsi method.
A13) Let 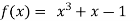
Now, 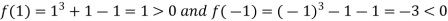
And also 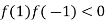
Hence the root of the equation 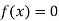 lies between
lies between 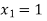 and
and 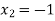 and so,
and so, 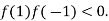
By Regula Falsi Method
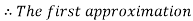
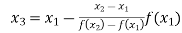
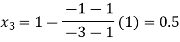
Now, 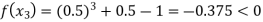
So, the root of the equation 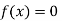 lies between 1 and 0.5 and so
lies between 1 and 0.5 and so 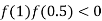
By Regula Fasli Method
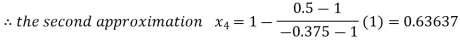
Now, 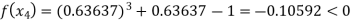
So, the root of the equation 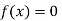 lies between 1 and 0.63637 and so
lies between 1 and 0.63637 and so 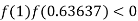
By Regula Fasli Method
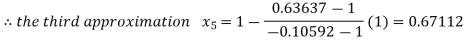
Now, 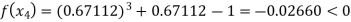
So, the root of the equation 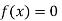 lies between 1 and 0.67112 and so
lies between 1 and 0.67112 and so 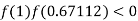
By Regula Fasli Method
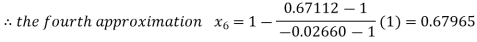
Now, 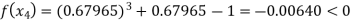
So, the root of the equation 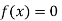 lies between 1 and 0.63636 and so
lies between 1 and 0.63636 and so 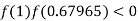
By Regula Fasli Method
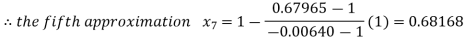
Now, 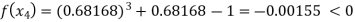
So, the root of the equation 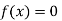 lies between 1 and 0.68168 and so
lies between 1 and 0.68168 and so 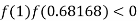
By Regula Fasli Method
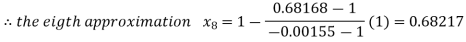
Now, 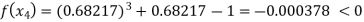
Hence the approximate root of the given equation near to 1 is 0.68217
Q14) Find the real root of the equation
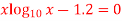
By the method of false position correct to four decimal places
A14) Let 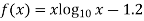
By hit and trail method
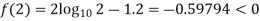
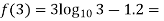 0.23136 > 0
0.23136 > 0
So, the root of the equation 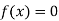 lies between
lies between 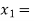 2 and
2 and 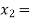 3 and also
3 and also 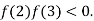
By Regula Falsi Method
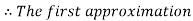
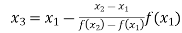
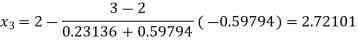
Now, 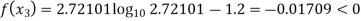
So, root of the equation 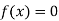 lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 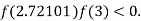
By Regula Falsi Method
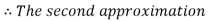
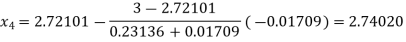
Now, 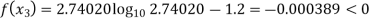
So, root of the equation 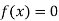 lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 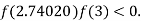
By Regula Falsi Method
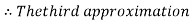
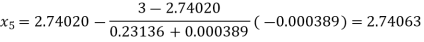
Now, 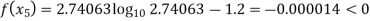
So, root of the equation 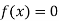 lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 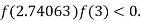
By Regula Falsi Method
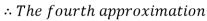
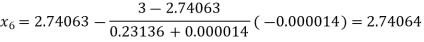
Hence the root of the given equation correct to four decimal places is 2.7406
Q15) Apply Regula Falsi Method to solve the equation
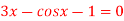
A15) Let 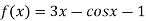
By hit and trail
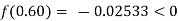
And 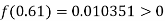
So, the root of the equation lies between 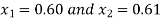 and also
and also 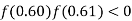
By Regula Falsi Method
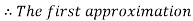
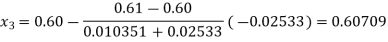
Now, 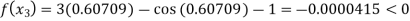
So, root of the equation 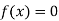 lies between 0.60709 and 0.61 and also
lies between 0.60709 and 0.61 and also 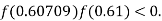
By Regula Falsi Method
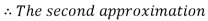

Now, 
So, root of the equation 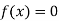 lies between 0.60710 and 0.61 and also
lies between 0.60710 and 0.61 and also 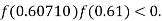
By Regula Falsi Method
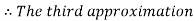

Hence the root of the given equation correct to five decimal place is 0.60710.
Q16) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places:  .
.
A16) Given 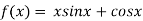
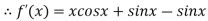
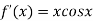
By Newton Raphson Method
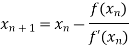
= 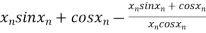
=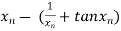
The initial approximation is 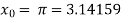 in radian.
in radian.
For n =0, the first approximation 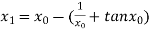
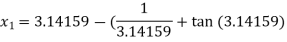
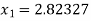
For n =1, the second approximation 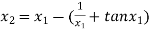
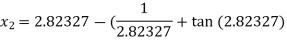
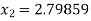
For n =2, the third approximation 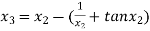
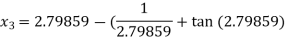
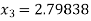
For n =3, the fourth approximation 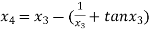
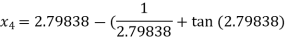
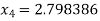
Hence the root of the given equation corrects to five decimal place 2.79838.
Q17) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 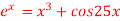 near to 4.5
near to 4.5
A17) Let
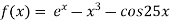
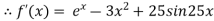
The initial approximation 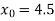
By Newton Raphson Method
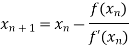
For n =0, the first approximation 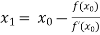
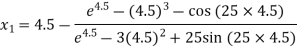
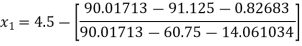
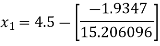
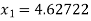
For n =1, the second approximation 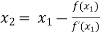
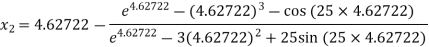
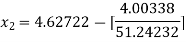
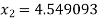
For n =2, the third approximation 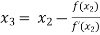
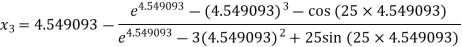
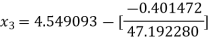
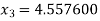
For n =3, the fourth approximation 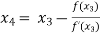
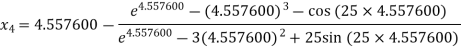
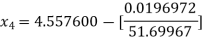
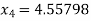
Hence the root of the equation correct to three decimal places is 4.5579
Q18) Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 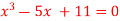
A18)
Let 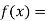
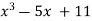
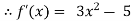
By Newton Raphson Method
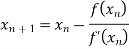
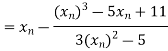
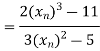
Let the initial approximation be 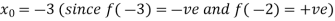
For n=0, the first approximation 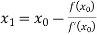
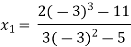
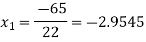
For n=1, the second approximation 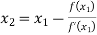
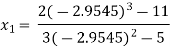
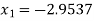
For n=2, the third approximation 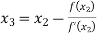
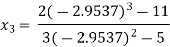
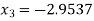
Since  therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Q19) Find the root of the equation 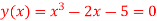 which lies between 2 and 3
which lies between 2 and 3
A19) Here let 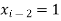 ,
, 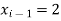 and
and 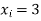 . Then
. Then 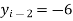
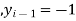 and
and 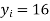
Hence
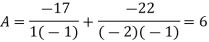
And
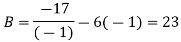
The quadratic equation is given by-
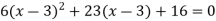
It gives the next approximation-
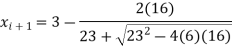
The positive sign is chosen as B is +ve,
Hence
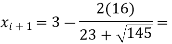
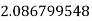
The error is calculated as-
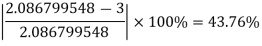
Here the error is large, so we do the next iteration-
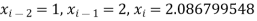
And
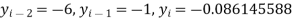
Now using these values, we get-
A = 5.086799558 and B = 10.96986336
The next approximation is-
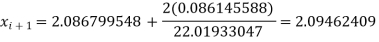
The error is 0.373553519%.
Q20) Find all the roots of polynomial equation 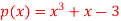 rounded off to three decimal places.
rounded off to three decimal places.
Stop the iteration if |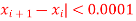
A20) The equation has three roots.
As there is only one change in the sign of the coefficient, by Descarts’ rule of sign the equation can have at most one positive real root.
The equation has no negative real roots since p(-x) = 0 has no change of sign of coefficients.
Here p(x) = 0 is of one degree, it has at least one real root.
So that the given equation has one positive real root and a complex pair.
Now let’s find the real roots by Birge-Vieta method-
The initial iteration is-
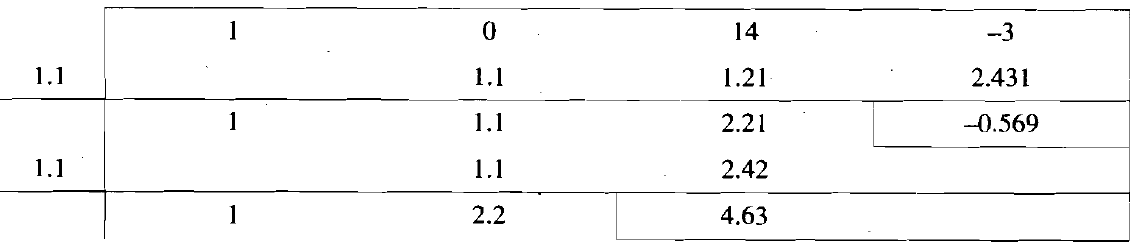
So that-
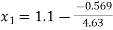 = 1.22289
= 1.22289
Similarly
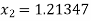
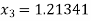
Here we see that 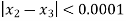 so that we stop the iteration.
so that we stop the iteration.
Hence the value of root is 1.213
Now we get the deflated polynomial of p(x).
In order to obtain deflated polynomial, we need to find the quadratic equation by using the final approximation. [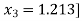

Here we notice p (1.213) = -0.0022,
That is, the magnitude of the error in satisfying p(x) = 0 is 0.0022.
We get-
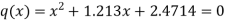
The roots of this quadratic equation are given by- [using quadratic equation]-
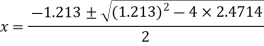
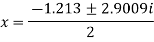
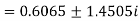
The three roots of the equation rounded off to three decimal places are 1.213, 0.6065+1.4505i and -0.6065 - 1.4505i