Unit-4
Solution of differential equations
Q1) Explain Picard’s method.
A1) Let us suppose the first order equation-
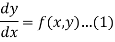
It is required to find out that particular solution of equation (1) which assumes the value 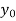 when
when 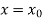 ,
,
Now integrate (1) between limits, we get-
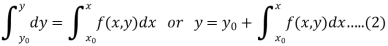
This is equivalent to equation (1),
For it contains the not-known y under the integral sign,
As a first approximation 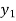 to the solution, put
to the solution, put  in f (x, y) and integrate (2),
in f (x, y) and integrate (2),
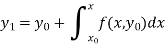
For second approximation-
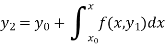
Similarly-
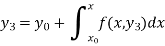
And so on.
Q2) Find the value of y for x = 0.1 by using Picard’s method, given that-
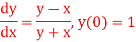
A2) We have-
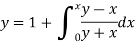
For first approximation, we put y = 1, then-

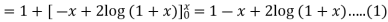
Second approximation-
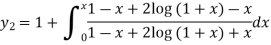
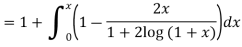
We find it very hard to integrate.
Hence, we use the first approximation and take x = 0.1 in (1)
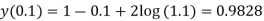
Q3) Use Euler’s method to find y (0.4) from the differential equation
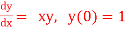 with h=0.1
with h=0.1
A3) Given equation 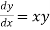
Here 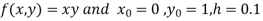
We break the interval in four steps.
So that 
By Euler’s formula
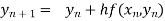 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
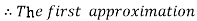
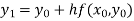
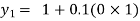
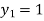
For n=1 in equation (i) we get
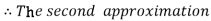
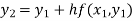
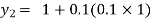
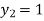 .01
.01
For n=2 in equation (i) we get
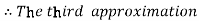
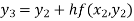
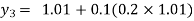
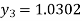
For n=3 in equation (i) we get
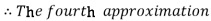
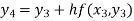
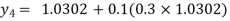
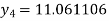
Hence y (0.4) =1.061106.
Q4) Using Euler’s method solve the differential equation for y at x=1 in five steps
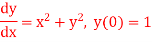
A4) Given equation 
Here 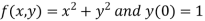
No. of steps n=5 and so that 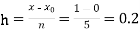
So that 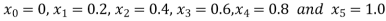
Also 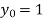
By Euler’s formula
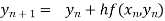 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
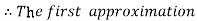
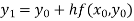
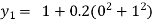

For n=1 in equation (i) we get
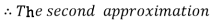
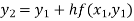
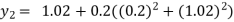
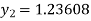
For n=2 in equation (i) we get
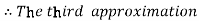
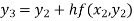
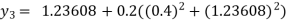

For n=3 in equation (i) we get
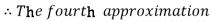
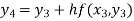
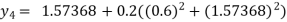
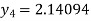
For n=4 in equation (i) we get
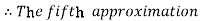
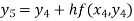
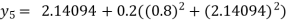

Hence 
Q5) Use modified Euler’s method to compute y for x=0.05. Given that

Result correct to three decimal places.
A5) Given equation 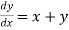
Here 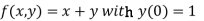
Take h =  = 0.05
= 0.05
By modified Euler’s formula the initial iteration is
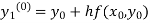
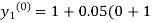 )
)
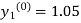
The iteration formula by modified Euler’s method is
 -----(i)
-----(i)
For n=0 in equation (i) we get

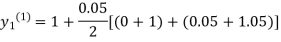
Where 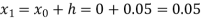 and
and 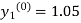 as above
as above
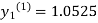
For n=1 in equation (i) we get
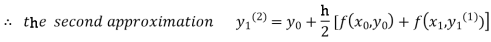
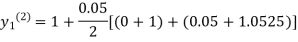

For n=3 in equation (i) we get
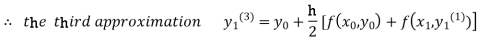
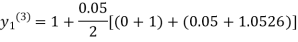
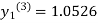
Since third and fourth approximation are equal.
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Q6) Using modified Euler’s method, obtain a solution of the equation
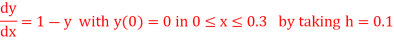
A6) Given equation 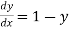
Here 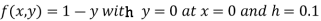
By modified Euler’s formula the initial iteration is
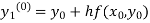
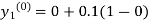
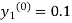
The iteration formula by modified Euler’s method is
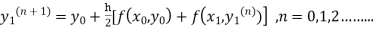 -----(i)
-----(i)
For n=0 in equation (I) we get
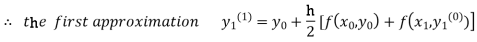
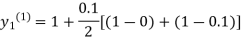
Where 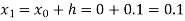 and
and 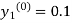 as above
as above

For n=1 in equation (i) we get
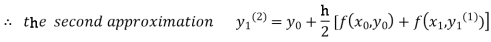
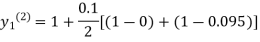

For n=2 in equation (i) we get
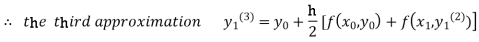
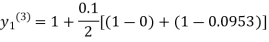
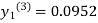
For n=3 in equation (i) we get
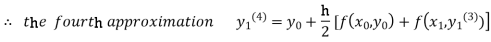
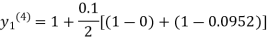
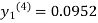
Since third and fourth approximation are equal.
Hence y=0.0952 at x=0.1
To calculate the value of  at x=0.2
at x=0.2
By modified Euler’s formula the initial iteration is
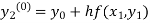
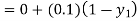
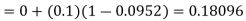
The iteration formula by modified Euler’s method is
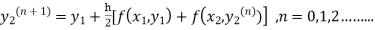 -----(ii)
-----(ii)
For n=0 in equation (ii) we get
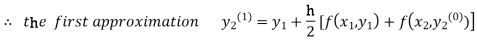
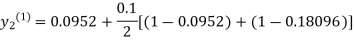
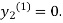 1814
1814
For n=1 in equation (ii) we get
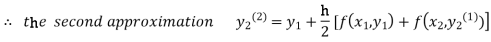
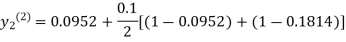
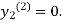 1814
1814
Since first and second approximation are equal.
Hence y = 0.1814 at x=0.2
To calculate the value of 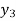 at x=0.3
at x=0.3
By modified Euler’s formula the initial iteration is
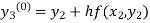
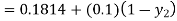
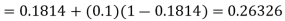
The iteration formula by modified Euler’s method is
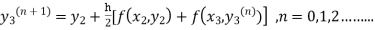 -----(iii)
-----(iii)
For n=0 in equation (iii) we get

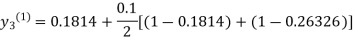
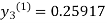
For n=1 in equation (iii) we get
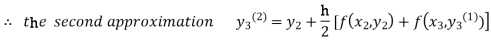
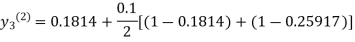
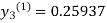
For n=2 in equation (iii) we get
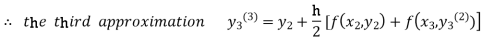
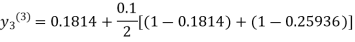
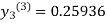
For n=3 in equation (iii) we get
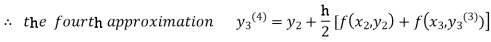
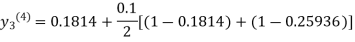
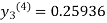
Since third and fourth approximation are same.
Hence y = 0.25936 at x = 0.3
Q7) Solve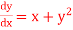 ,
, 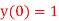 using Taylor’s series method and compute
using Taylor’s series method and compute 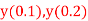 .
.
A7) Here 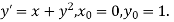 This implies that
This implies that 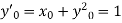 .
.
Differentiating, we get
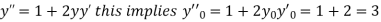 .
.
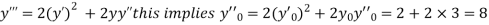 .
.
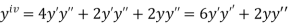
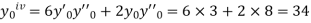 .
.
The Taylor’s series at  ,
,
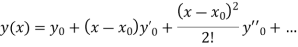
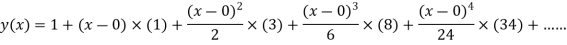
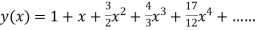 (1)
(1)
At 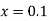 in equation (1) we get
in equation (1) we get
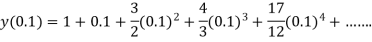
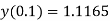
At 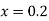 in equation (1) we get
in equation (1) we get
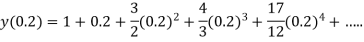
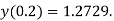
Q8) Using Taylor’s series method, find the solution of

At  ?
?
A8) Here 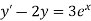
At 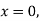 implies that
implies that 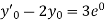 or
or 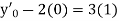 or
or 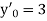
Differentiating, we get
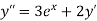 implies that
implies that  or
or 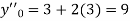 .
.
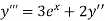 implies that
implies that 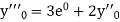 or
or 
 implies that
implies that  or
or 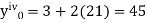
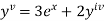 implies that
implies that 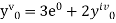 or
or 
The Taylor’s series at 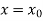 ,
,
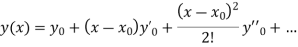
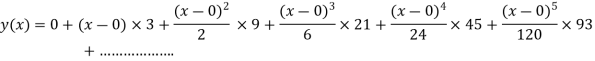
 (1)
(1)
At  in equation (1) we get
in equation (1) we get
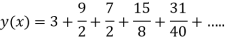
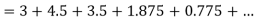
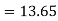
At 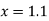 in equation (1) we get
in equation (1) we get
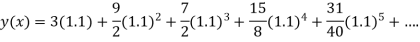
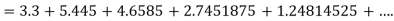
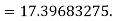
Q9) Write down the fourth order Runge kutta method.
A9) A fourth order Runge Kutta formula:
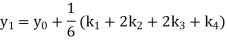
Where 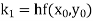
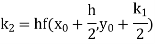
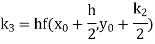

Q10) Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that
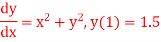
A10) Given equation 
Here 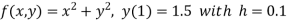
Also 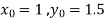
By Runge Kutta formula for first interval
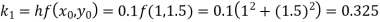
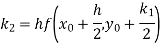
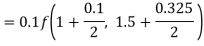
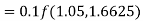

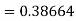
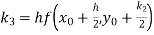
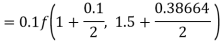
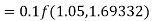
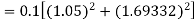
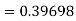
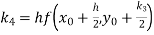

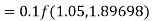
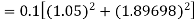

Again 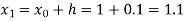
A fourth order Runge Kutta formula:
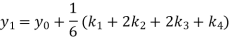
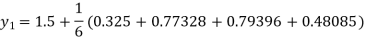
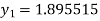
To find y at 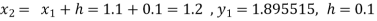
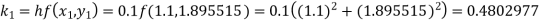
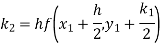
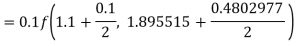
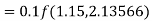
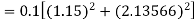
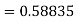
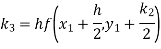
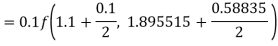
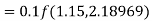
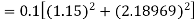
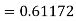
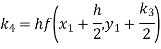
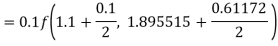
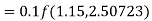
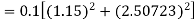
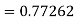
A fourth order Runge Kutta formula:

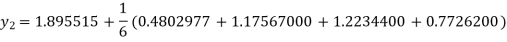
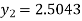
Q11) Apply Runge Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if

A11) Given equation 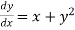
Here 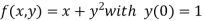
Also 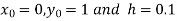
By Runge Kutta formula for first interval
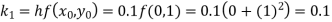
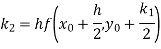

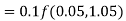

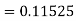

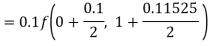
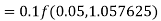

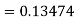
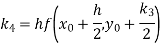
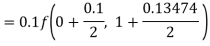
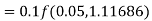
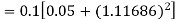
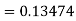
A fourth order Runge Kutta formula:
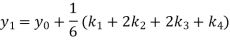

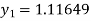
Again 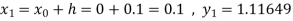
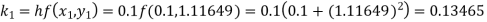
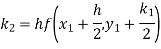

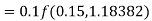
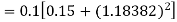
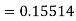
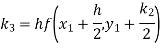
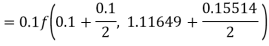
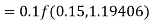
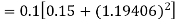
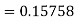
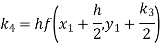
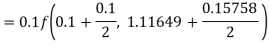
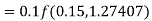
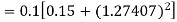
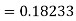
A fourth order Runge Kutta formula:

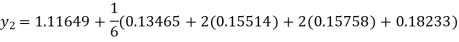
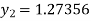
Q12) Using Runge Kutta method of fourth order, solve
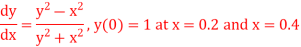
A12) Given equation 
Here 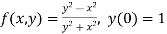
Also 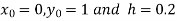
By Runge Kutta formula for first interval
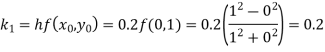
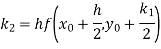
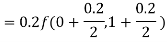
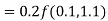
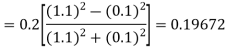
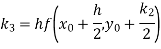
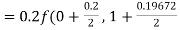 )
)
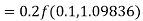
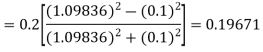

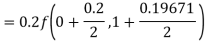
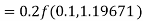
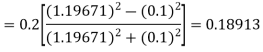
A fourth order Runge Kutta formula:
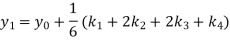
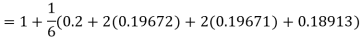
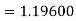
Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 


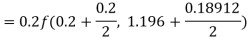
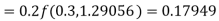
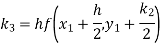

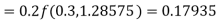
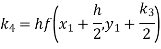
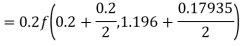
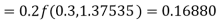
A fourth order Runge Kutta formula:
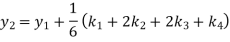
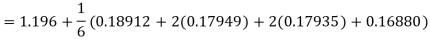
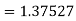
Hence at x = 0.4 then y=1.37527
Q13) Using Runge Kutta method of order four, solve  to find
to find 
A13) Given second order differential equation is
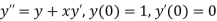
Let 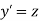 then above equation reduces to
then above equation reduces to
Or 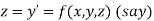
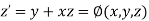 (say)
(say)
Or 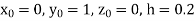 .
.
By Runge Kutta Method we have
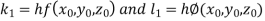
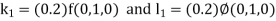
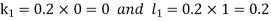

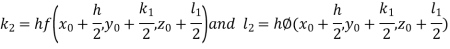
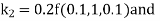
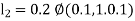

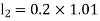
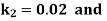

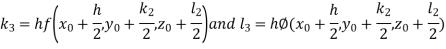
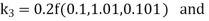
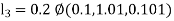
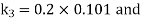
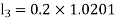
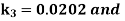

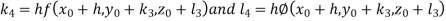



A fourth order Runge Kutta formula:

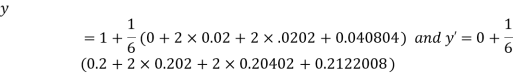
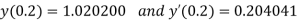
Q14) Using Runge Kutta method, solve
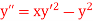 for
for 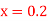 correct to four decimal places with initial condition
correct to four decimal places with initial condition 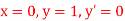 .
.
A14) Given second order differential equation is
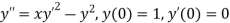
Let 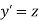 then above equation reduces to
then above equation reduces to
Or 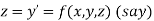
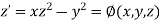 (say)
(say)
Or 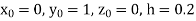 .
.
By Runge Kutta Method we have
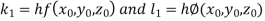

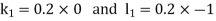
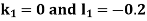

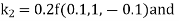
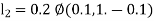
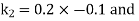
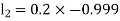

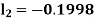
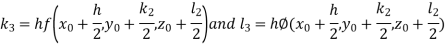
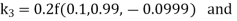

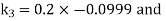
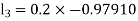
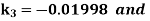
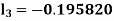
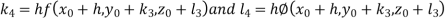

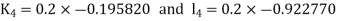

A fourth order Runge Kutta formula:
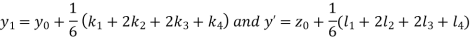
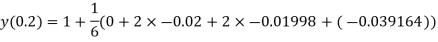
And
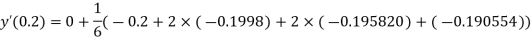
 .
.
Q15) Solve the differential equations
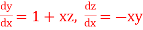 for
for 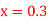
A15) Using four order Runge Kutta method with initial conditions 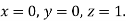
Given differential equation are
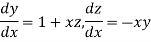
Let 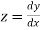
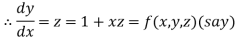
And 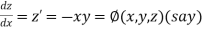
Also 
By Runge Kutta Method we have

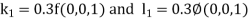
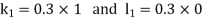
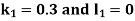
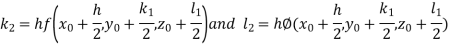
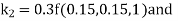
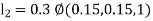
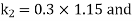
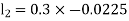

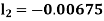
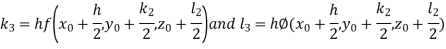
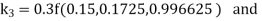
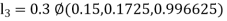
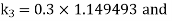
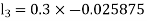
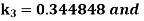
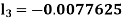
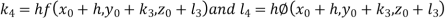
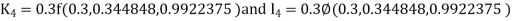
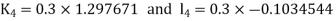

A fourth order Runge Kutta formula:
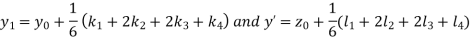
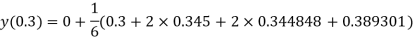
And 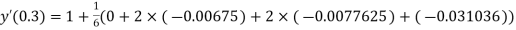
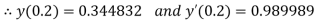 .
.
Q16) What are Adams - Bashforth predictor formula and Adams - Bashforth corrector formula.
A16) Adams - Bashforth predictor and corrector formula-
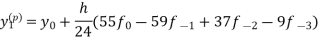
This is called Adams - Bashforth predictor formula.
And

This is called Adams - Bashforth corrector formula.
Q17) Find the solution of the differential equation 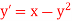 in the range
in the range 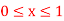 for the boundary conditions y = 0 and x = 0 by using Milne’s method.
for the boundary conditions y = 0 and x = 0 by using Milne’s method.
A17) By using Picard’s method-
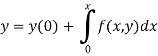
Where
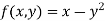
To get the first approximation-
We put y = 0 in f (x, y),
Giving-
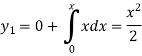
In order to find the second approximation, we put y = 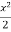 in f (x, y)
in f (x, y)
Giving-
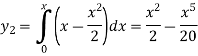
And the third approximation-
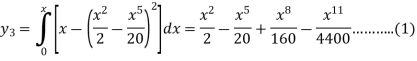
Now determine the starting values of the Milne’s method from equation (1), by choosing h = 0.2

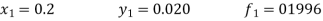
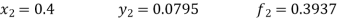
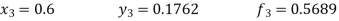
Now using the predictor-
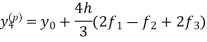
X = 0.8
 ,
, 
And the corrector-
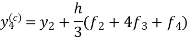
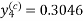 ,
, 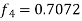 ................(2)
................(2)
Now again using corrector-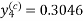
Using predictor-
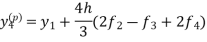
X = 1.0,
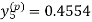 ,
, 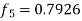
And the corrector-
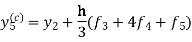
 ,
, 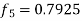
Again, using corrector-
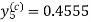 , which is same as before
, which is same as before
Hence
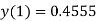
Q18) A second order Runge Kutta formula is-
A18) A second order Runge Kutta formula
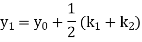
Where 
Rewrite as
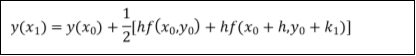
Q19) Explain Taylor’s series method.
A19) Taylor’s Series Method:
The general first order differential equation
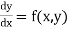 …. (1)
…. (1)
With the initial condition 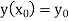 … (2)
… (2)
Let 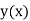 be the exact solution of equation (1), then the Taylor’s series for
be the exact solution of equation (1), then the Taylor’s series for 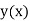 around
around 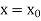 is given by
is given by
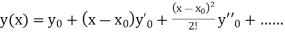 (3)
(3)
If the values of  are known, then equation (3) gives power series for y. By total derivatives we have
are known, then equation (3) gives power series for y. By total derivatives we have
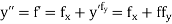 ,
,
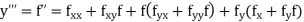

And other higher derivatives of y. The method can easily be extended to simultaneous and higher –order differential equations. In general,
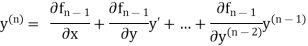
Putting 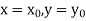 in these above results, we can obtain the values of
in these above results, we can obtain the values of 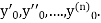 finally, we substitute these values of
finally, we substitute these values of 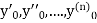 in equation (2) and obtain the approximate value of y; i.e., the solutions of (1).
in equation (2) and obtain the approximate value of y; i.e., the solutions of (1).
Q20) Explain Euler’s method.
A20) In this method the solution is in the form of a tabulated values
Integrating both side of the equation (i) we get
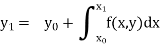
Assuming that 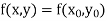 in
in 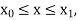 this gives Euler’s formula
this gives Euler’s formula
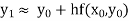
In general formula
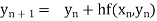 , n=0,1, 2….
, n=0,1, 2….
Error estimate for the Euler’s method