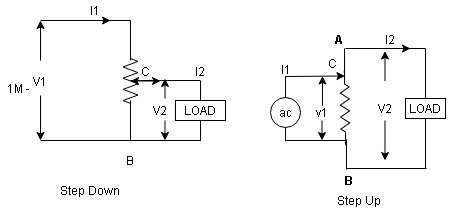
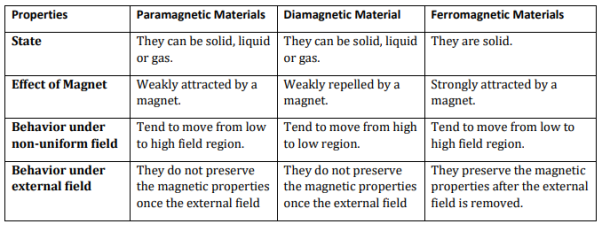
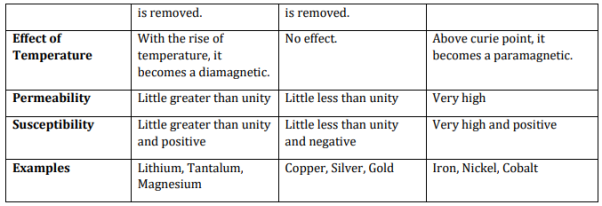
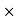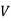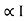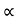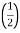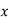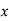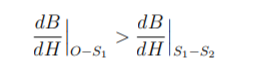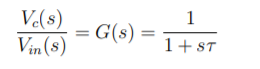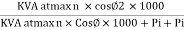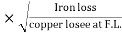Auto Transformer

An auto Transformer is a special type of transformer such that a part of the winding is common to both primary as well as secondary

It has only One winding wended on a laminated magnetic core

With the help of auto Transformer, the voltage can be stepped up and stepped down at any desired value

Fig A shows auto T/F as step down T/F variable terminal B C is connected to load and it acts as secondary wdg.

The position of point C is called as topping point can be selected as per requirement

Fig. B show auto T/F as step up T/F variable terminal B C is connected to supply side i.e. ac side and it acts as secondary winding

The operating principle of auto Transformer is same as that of 2 winding Transformer

Advantages

1. Weight of copper required in an auto Transformer is always loss than that of the conventional  2 winding Transformer and hence it is chaper
2. Compact in size and loss costly.
3. Losses taking place in Transformer is reduced hence efficiency is higher than conventional Transformer.
4. Due to reduced resistance, voltage, regulation is better than conventional T/F.

Disadvantages:

As low voltage and high voltage sides are not separate then there is always risk of electric shocks when use for high vtg. Applications

Applications

1. Starting squirrel cage induction motor and synchronous motor.
2. Auto transformer as dimmer stat
3. Used as variable ac to variable ac Voltage

There are 2 types of losses occurring in a transformer

A)    1. Core loss or Iron loss

B)    2. Copper loss

• Core losses:

1. This loss is due to the reversal of flux
2. The flux set up in the core is dependent on the i/p supply as the i/p supply is constant in magnitude the flux set up will be constant and core losses are also constant.
3. Core losses are voltage dependent loss they can be subdivided in 2

1 Hysteresis loss

2 reedy current loss

1. Hysteresis loss : The iron loss occurring in the core of T/F due to the Hysteresis curve of the magnetic material used for core is called as Hysteresis loss.

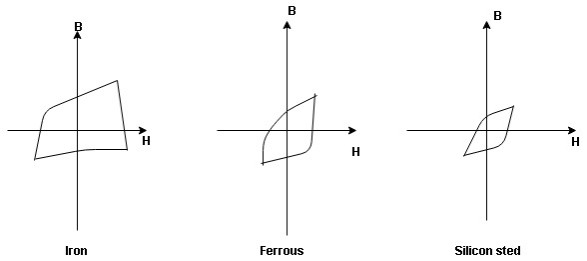
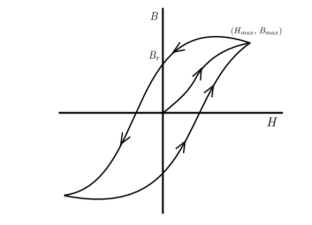
Hysteresis curve is the curve as loop which shows the properly of magnetic material to lag the flux density B behind the field Intensely  H

Above is the 3 different loops (Hysteresis of 3 diff. Materials)

the selection of magnetic material for the construction of core depends upon Hysteresis loop of that material having tall and narrow Hysteresis loop is selected for the T/F core

silicon Steel

Hysteresis loss depends on fold factor

PH = KH. Bm1.67 F V – watts

Where KH = constant (Hyst)

Bm = max Flux density

F = Frequency

= Volume of core.

2.     Reedy current loss :

This loss is due to the flow of reedy (circular) current in the core caused by induced emf in core

PE = Ke Bm2 f2 t2 v – watts

Where

Ke = reedy current const.

t = thickness of core

It can be reduced by using stacks of laminations instead of solid core

B]   Copper loss : PCU

 The Copper loss is due to resistance of the primary and secondary winding

  It is load dependent / current dependent loss

As load on a transformer is variable (changing) current changes copper loss is a variable loss

                      Primary       secondary

Total C is loss = I12R12  +  I22 R22

Copper loss depends upon load on T/F and is proportional to square of load current or KVA rating of transformer

PCU 2 (KVA)2

F.L = full load

PCU (at half load) = 2 PCu F.L

= (0.5)2  PCU F.L.

Or PCu ( load)  = ()2 PCu F.L

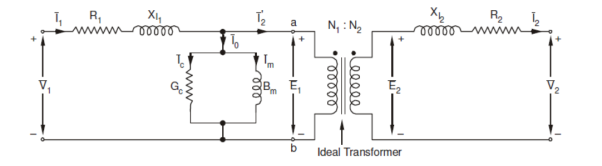
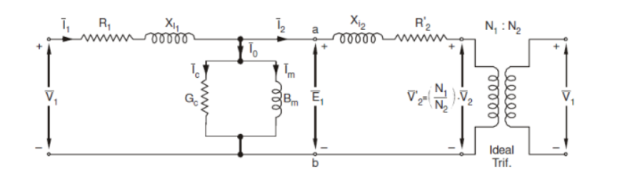
The excitation current I0‾ can be divided into two components Im‾ and Ii‾.

 Im‾ is its magnetizing component that creates mutual flux Φ‾, and

Ii‾ is the core loss component that provides the loss associated with alternating of the flux.

It can be represented as
I0‾ = Im‾ + Ii‾

Here vector form is indicated by the negative (‾) symbol.

Hence, the equivalent circuit of a practical transformer can be represented as shown in the figure below

Here,
Gc = conductance
Bm = Susceptance

The impedance can now be referred to the primary side resulting in the following circuit:

                                                     Equivalent circuit referred to primary

X l2’ = (N1/N2)2 X l2
R2’ = (N1/N2)2 R2

The load voltage and currents referred to primary side are:

V2’ = (N1/N2) V2
I2’ = (N1/N2) I2

V1’ = (N1/N2) V1
I1’ = (N1/N2) I1
Gi’= (N1/N2)2 Gi
Bi’= (N1/N2)2 Bi
X l1’ = (N1/N2)2 X l1
R1’ = (N1/N2)2 R1

An ideal transformer is one that has

1. no winding resistance
2. no leakage flux i.e., the same flux links both the windings
3. no iron losses (i.e., eddy current and hysteresis losses) in the core

Although an ideal transformer cannot be physically realized, yet its study provides a very powerful tool in the analysis of a practical transformer. In fact, practical transformers have properties that approach very close to an ideal transformer.

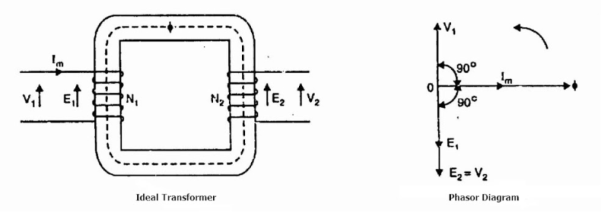
Consider an ideal transformer on no load i.e., the secondary is open-circuited as shown in the figure. Under such conditions, the primary is simply a coil of pure inductance.

When an alternating voltage V₁ is applied to the primary, it draws a small magnetizing current Iₘ which lags behind the applied voltage by 90°. This alternating current Iₘ produces an alternating flux ϕ which is proportional to and in phase with it.

The alternating flux ϕ links both the windings and induces e.m.f. E₁ in the primary and e.m.f. E₂ in the secondary. The primary e.m.f. E₁ is, at every instant, equal to and in opposition to V₁  (Lenz’s law). Both e.m.f.sE₁, and E₂ lag behind flux ϕ by 90°. However, their magnitudes depend upon the number of primary and secondary turns.

Phasor Diagram of Ideal Transformer

The phasor diagram of an ideal transformer on no load is also shown above. Since flux ϕ is common to both the windings, it has been taken as the reference phasor.

The primary e.m.f. E₁ and secondary e.m.f. E₂ lag behind the flux ϕ by 90°.

Note that E₁ and E₂ are in phase. But E₁ is equal to V₁ and 180° out of phase with it.

Practical Transformer

A practical transformer differs from the ideal transformer in many respects. The practical transformer has,

1. iron losses,
2. winding resistances and,
3. magnetic leakage, giving rise to leakage reactance.

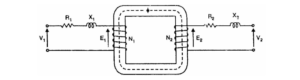
1. Iron Losses

Since the iron core is subjected to alternating flux, there occurs eddy current and hysteresis loss in it. These two losses together are known as iron losses or core losses.

The iron losses depend upon the supply frequency, the maximum flux density in the core, volume of the core, etc.

It may be noted that the magnitude of iron losses is quite small in a practical transformer.

2. Winding resistances

Since the windings consist of copper conductors, it immediately follows that both primary and secondary will have winding resistance. The primary resistance R₁ and secondary resistance R₂ act in series with the respective windings as shown in the figure.

When current flows through the windings, there will be power loss as well as a loss in voltage due to IR drop. This will affect the power factor and E₁ will be less than V₁ while V₂ will be less than E₂.

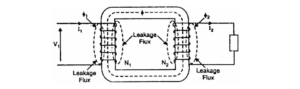
3. Leakage reactances

Both primary and secondary currents produce flux. The flux ϕ which links both the windings is the useful flux and is called mutual flux.

However, the primary current would produce some flux ϕ which would not link the secondary winding. Similarly, the secondary current would produce some flux ϕ that would not link the primary winding.

The flux such as ϕ₁ or ϕ₂ which links only one winding is called leakage flux. The leakage flux paths are mainly through the air. The effect of these leakage fluxes would be the same as though inductive reactance were connected in series with each winding of the transformer that had no leakage flux as shown in the figure.

In other words, the effect of primary leakage flux ϕ₁ is to introduce an inductive reactance X₁ in series with the primary winding as shown. Similarly, the secondary leakage flux ϕ₂ introduces an inductive reactance X₂ in series with the secondary winding.

There will be no power loss due to leakage reactance. However, the presence of leakage reactance in the windings changes the power factor as well as there is voltage loss due to IX drop.

Note.
Although leakage flux in a transformer is quite small (about 5% of ϕ)  compared to the mutual flux ϕ, yet it cannot be ignored.

It is because leakage flux paths are through the air of high reluctance and hence require considerable e.m.f. It may be noted that energy is conveyed from the primary winding to the secondary winding by mutual flux f which links both the windings.

The rms voltage induced in a transformer is given by E = 4.44φmfN ---------(1)

where, φm is maximum value of the flux in the core, f is operating frequency and N is number of turns in the coil.

This flux in the coil is given by φm = BmAc ----------(2)

where, Bm is the maximum flux density in core and Ac is the cross-sectional area of the core.

So, we have E = 4.44BmAcfN -----------------(3)

The value of induced voltage E is thus dependent upon Bm which can be setup in the core.

From Biot-Savart’s law that a current carrying conductor produces magnetic field.

“Magnetic field strength” H is proportional to the current which produces the field.

From Ampere’s Circuital law, it can be proved that H is proportional to current I.

If a current carrying coil produces magnetic flux which traverses an average length of l in complete flux path, then

Hl = NI -------------------------------(4)

In a magnetic circuit, this field is represented by magnetomotive force. It is analogous to the electromotive force in electrical circuit. This field is responsible to “set up” certain flux, which in turn gives rise to certain flux density B.

The amount of flux which can be setup in a material is determined by an inherent property of the material, called as permeability, denoted by

µ. B = µH --------------------------------(5)

Let us consider materials used in the laminations of transformers. They are called ferromagnetic materials. A piece of ferromagnetic material is composed of several “domains”. In each domain, magnetic moments of all atoms are aligned in one direction. In general, the domains are randomly oriented.

When external magnetic field H is applied to a material, all the domains align in a particular direction, setting up “net flux” in the material. Due to domain alignment B (i.e. the magnitude of B) increases. However, after a certain value of B, the slope of B − H curve starts reducing as shown in Fig. 1;

O − S1 represents the linear region and

S1 − S2 represents the “saturation region”.

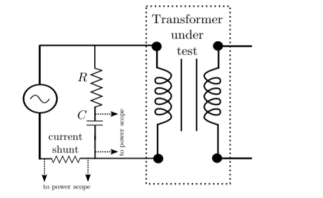
From Faraday’s law,

V = N dφ /dt

B is directly proportional to flux φ. A signal proportional to B can be obtained by integrating the voltage signal. The voltage can be integrated approximately by using an RC circuit.

The transfer function of the circuit is given by

The time constant τ = RC should be chosen such that, in frequency domain (1 + jωτ ) ≈ jωτ

            Hysteresis loop

Equation 4 tells that H is is proportional to current. The two signals can be given to two channels of a digital storage oscilloscope. B − H curve of the material can be seen.

The efficiency of T/F is maximum when copper loss equates iron loss this is the condition for max efficiency

ie  Pi = PCU

=

PCU = Pi at max n

Where KVA at max n given = Full load KVA