Unit-1

Ordinary Differential Equation of Higher Order

Q1: Solve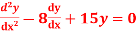

A1. Given,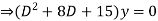

Here Auxiliary equation is

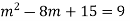
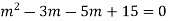
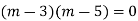
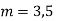
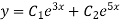
Q2: Solve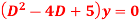

A2. Auxiliary equation are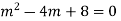

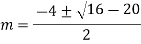
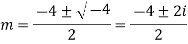
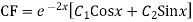
Q3:

A3. Auxiliary equation are

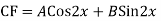
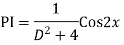
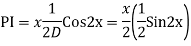
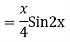
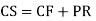
Q4: Solve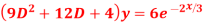

A4. The AE is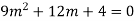

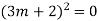
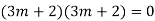
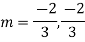
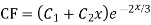
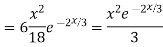
Complete solution y= CF + PI

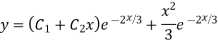
Q5: Solve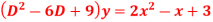

A5. The AE is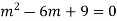

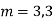
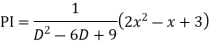
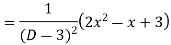
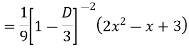
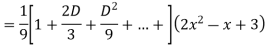
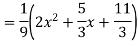
Complete solutio0n is y= CF + PI

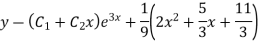
Q6: Solve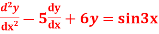

A6. Given equation in symbolic form is

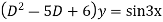
Its Auxiliary equation is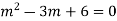

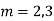
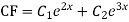
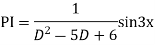
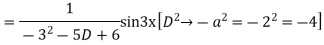
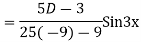
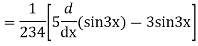
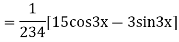
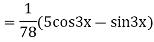
Complete solution is y= CF + PI

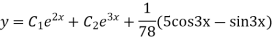
Q7: Solve the following simultaneous differential equations-

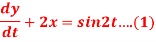
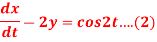
Given that x(0)=1  and y(0)= 0

A7:

Consider the given equations,

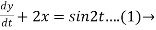Dy +2x = sin2t

Dx -2y = cos2t

By solving the above equations we get,

(D2 +4)Y =0

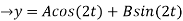
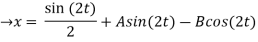
X(0) = 1, y(0) = 0

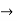A =0, B=-1

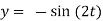
Q8: Solve (D – D’ – 2 ) (D – D’ – 3) z =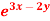

A8:.

The C.F. will be given by-

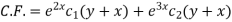
Particular integral-

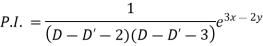
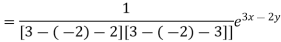
Therefore the complete solution is-

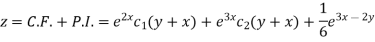
Q9: Find P.I. of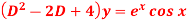

A 9:. P.I =

Replace D by D+1

Put

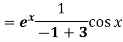
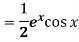
Q10: Solve-

A 10:

Here P = cot x and Q =

Choosing z so that

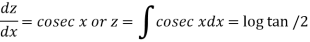
Changing the independent variable x to z, we get-

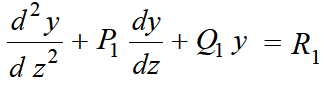......(1)

Where-

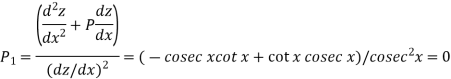
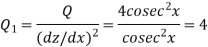
Equation(1) becomes-

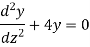
Its sol. Is-

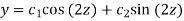
i.e.

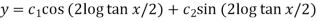
Which is the required solution

Q11: Solve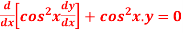

A11:

Here we have-

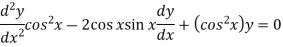
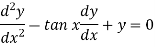
Here,

P = -2 tan x, Q = 1, R = 0

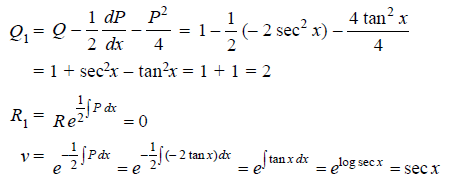
Normal equation is-

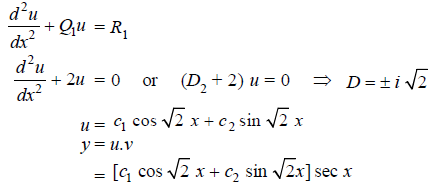
Q12: Solve

A12:. As it is a Cauchy’s homogeneous linear equation.

Put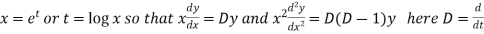

Then the equation becomes [D(D-1)-D+1]y = t   or

Auxiliary equation-

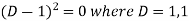
So that-

   C.F.=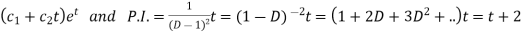

Hence the solution is- 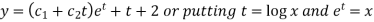, we get-

Q13: Solve

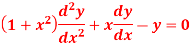
Sol.

Here we have-

Let the solution of the given differential equation be-

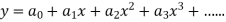
Since x = 0 is the ordinary point of the given equation-

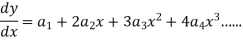
Put these values in the given differential equation-

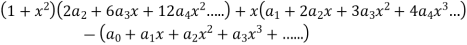
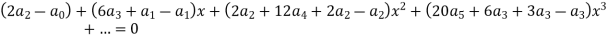
Equating the coefficients of various powers of x to zero, we get-

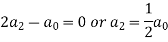
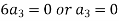
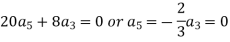
Therefore the solution is-

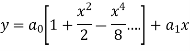
Q13: Find solution in generalized series form about x = 0 of the differential equation

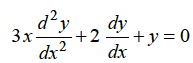
A13:

Here we have

………… (1)

Since x = 0 is a regular singular point, we assume the solution in the form

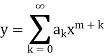
So that

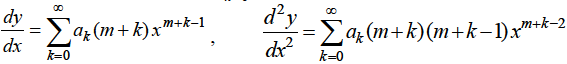
Substituting for y, in equation (1), we get-

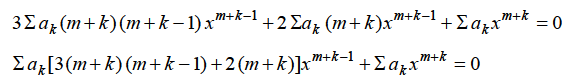…..(2)

The coefficient of the lowest degree term 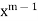in (2) is obtained by putting k

= 0 in first summation only and equating it to zero. Then the indicial equation is

Since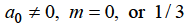

The coefficient of next lowest degree term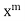in (2) is obtained by putting

k = 1 in first summation and k = 0 in the second summation and equating it to zero.

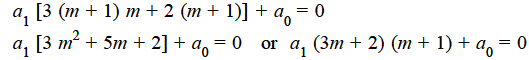
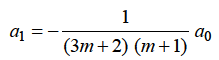
Equating to zero the coefficient of the recurrence relation is given by

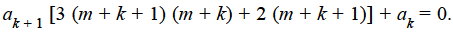
Or

Which gives-

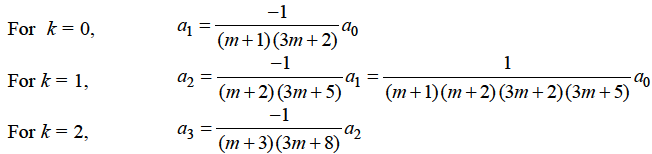
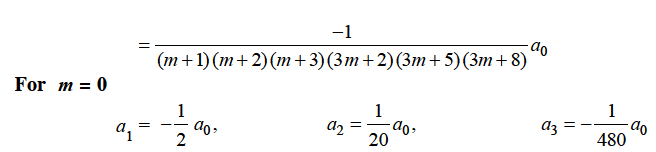
Hence for-

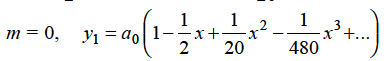
Form m = 1/3-

Hence for m = 1/3, the second solution will be-

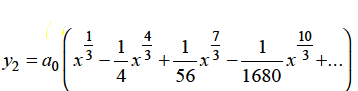
The complete solution will be-