Unit-3

Sequences and Series

Q1: Consider a sequence 2, 3/2 , 4/3 , 5/4, …….. here Sn =  1 + 1/n

A1. As we can see that the sequence Sn is convergent and has limit 1.

According to def.

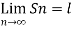
Q2: Check whether the series 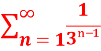 is convergent or divergent. Find its value in case of convergent.

A2. The general formula for this series is given by,

Sn =  = )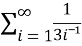

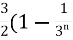           We get,

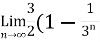) = 3/2

Hence the series is convergent and its values is 3/2.

Q3: Check whether the following series is convergent or divergent. If convergent, find its value.

A3. n’th term of the series will be,

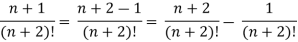
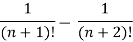
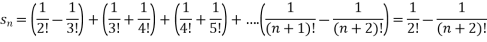
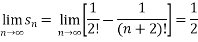
Q4: Test the convergence of the series-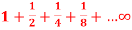

A4. Here we can see that the given series is in geometric progression

As its first term is 1 and common ratio is ½.

Then we know that the sum of n terms of a geometric progression is-

Hence the limit will be-

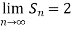
So that the series is convergent.

Q5: Test the convergence of the following series.

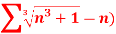
A5. We have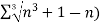  

First we will find 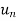 and the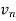

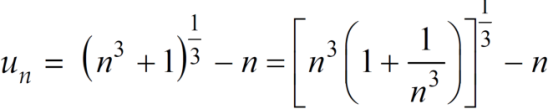
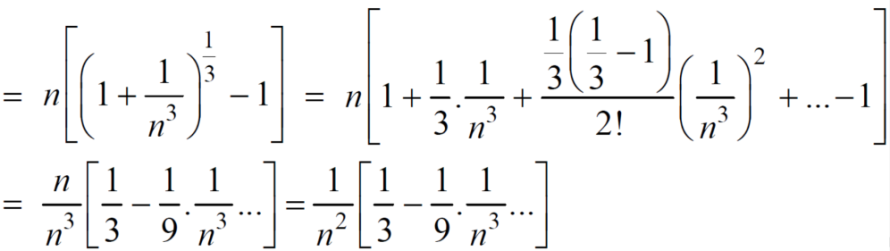
And

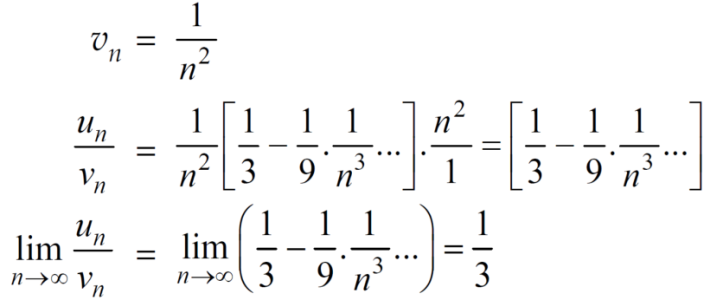
Here, we can see that, the limit is finite and not zero,

Therefore, and converges or diverges together.

Since is of the form 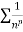 where p = 2>1

So that , we can say that,

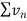is convergent , so that 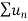will also be convergent.

Q6: Test the convergence of the series whose n’th term is given below-

n’th term =

A6. We have

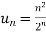  and

By D’Alembert ratio test,

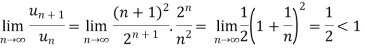
So that by D’Alembert ratio test , the series will be convergent.

Q7: Test for the convergence of the n’th term of the series given below-

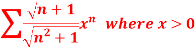
A7. We have ,

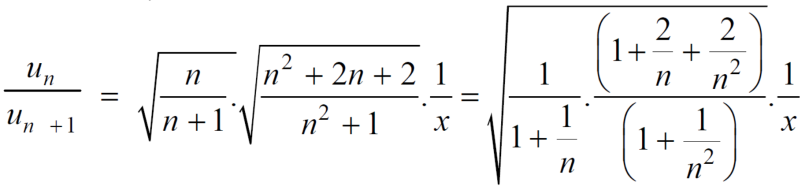
Now , by D’Almbert ratio test 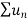converges if 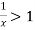and diverges if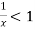 

At x = 1 , this test fails.

Now , when x = 1

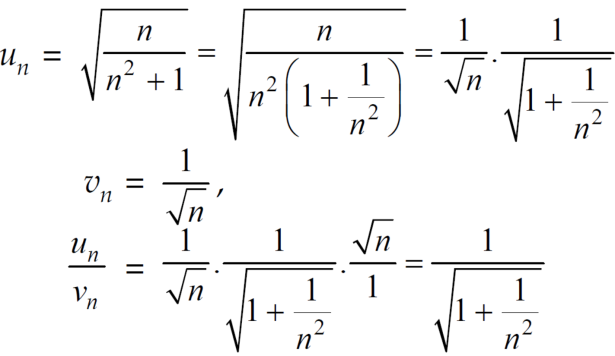
The limit is finite and not zero.

Then by comparison test, converges or diverges together.

Since 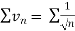is the form of , in which

Hence diverges then will also diverge.

Therefore in the given series 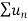converges if x<1 and diverges if x≥1.

Q8: Find the fourier series of the function f(x) = x      where 0 < x < 2 π

A8. We know that, from fourier series,

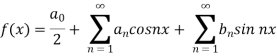
first we will find ,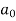

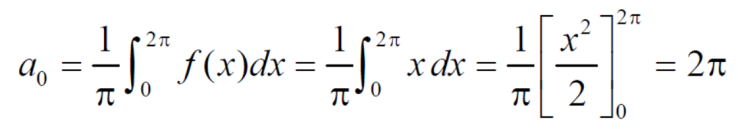
Now,

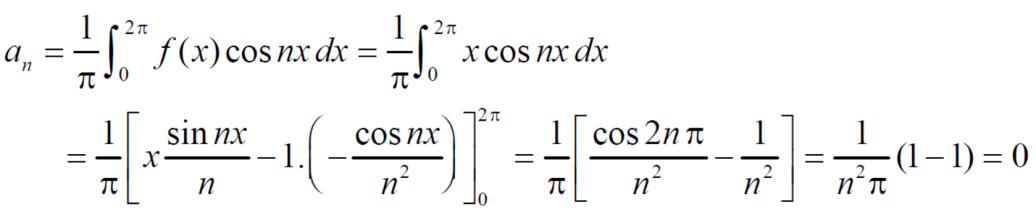
And ,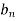

Put these value in fourier series, we get

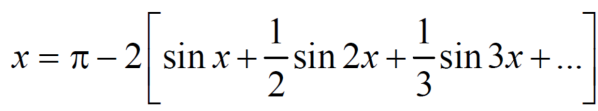
Q9: Find the Fourier series for f(x) = 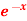in the interval .

A9.

Suppose

Then-

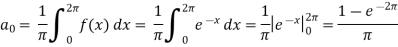
And

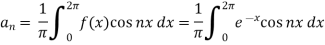
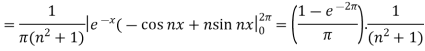
So that-

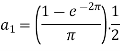
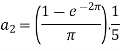
And then-

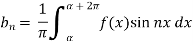
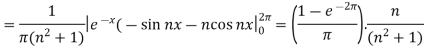
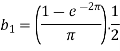
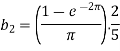
Now put these value in equations (1), we get-

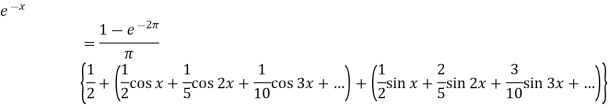
Q10: Find the Fourier series expansion of the periodic function of period 2π.

f(x) = x² ,    -π≤x≤π

A10. The given function is even, so that,

We will find

The Fourier series will be,

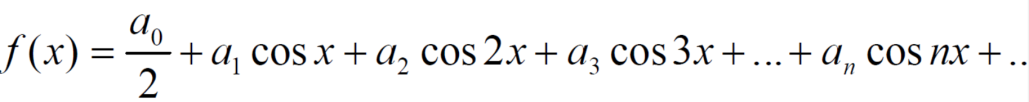
Q11: Find the Fourier sine series for the function-

Where ‘a’ is a constant.

A11. here we know-

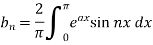
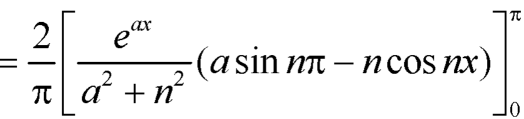
We know that-

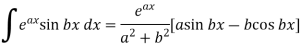
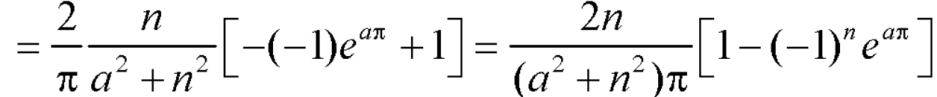
And