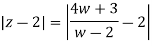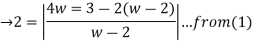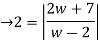Unit-4
Complex Variable – Differentiation
Q1: Find-
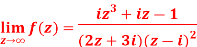
A1. Here we have-

Divide numerator and denominator by  , we get-
, we get-

Q2: If w = log z, then find 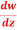 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
A2. Here we have 
Therefore-
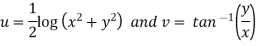
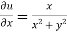 and
and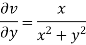
Again-

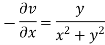
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0
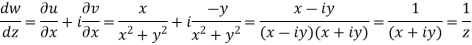
Q3: Prove that the function 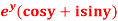 is an analytical function.
is an analytical function.
A3. Let 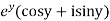 =u+iv
=u+iv
Let 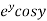 =u and
=u and 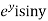 =v
=v


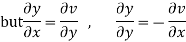
Hence C-R-Equation satisfied.
Q4: Prove that 
A4. Given that
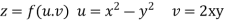


Since 

V=2xy

Now 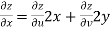

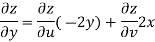
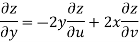
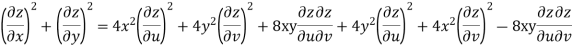
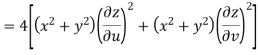
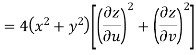
But 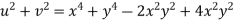
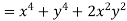
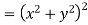

Hence 
Q5: Prove that  and
and 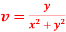 are harmonic functions of (x, y).
are harmonic functions of (x, y).
A5.
We have 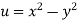
Now
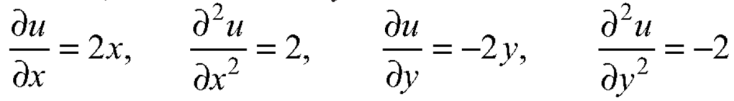
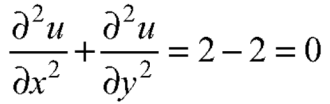
Here it satisfies Laplace equation so that u (x, y) is harmonic.
Now-
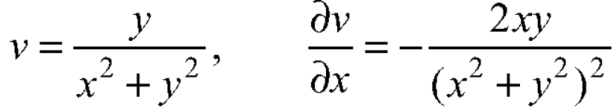

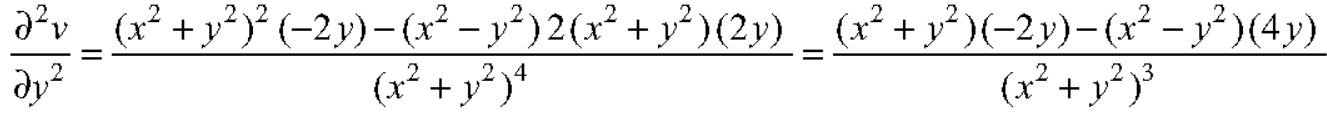
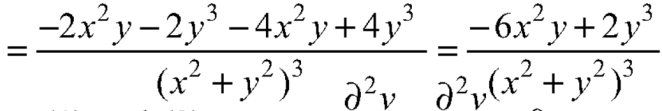
On adding the above results-
We get-
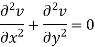
So that v(x, y) is also a harmonic function.
Q6: Find the harmonic conjugate function of the function U (x, y) = 2x (1 – y).
A6.
We have,
U(x, y) = 2x (1 – y)
Let V is the harmonic conjugate of U.
So that by total differentiation,
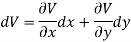


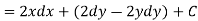
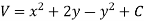
Hence the harmonic conjugate of U is 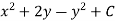
Q7: If

Then find f(z)
A7.
Here-

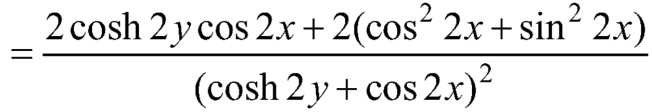
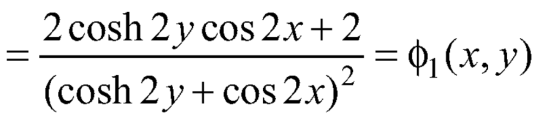
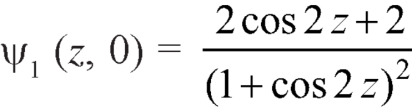


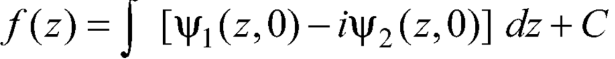
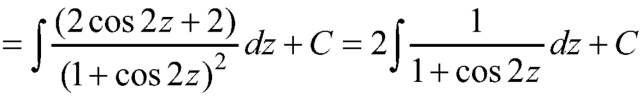

Which is the required answer.
Q8: Show that the mapping 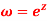 is conformal in the whole of the z plane.
is conformal in the whole of the z plane.
A8.
Let z=x+iy
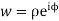
Then 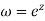
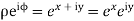
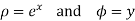
Consider the mapping of the straight line x=a in z plane the w plane which gives 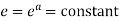 which is a circle in the w plane in the anticlockwise direction similarly the straight line y=b is mapped into
which is a circle in the w plane in the anticlockwise direction similarly the straight line y=b is mapped into 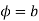 which is a radius vector in the w plane.
which is a radius vector in the w plane.
The angle between the line x=a and y=b in the z plane is a right angle. The corresponding angle in the w plane between the circle e = constant and the radius vector 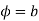 is also a right angle which establishes that the mapping
is also a right angle which establishes that the mapping 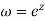 is conformal.
is conformal.
Q9: Show that the curve u = constant and v = constant cut orthogonally at all intersections but the transformation w = u + iv is not conformal. Where-
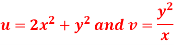
A9.
Let  …………. (1)
…………. (1)
Differentiate (1), we get-
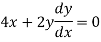
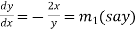 …………… (2)
…………… (2)
Now-
 …………….. (3)
…………….. (3)
Differentiate (3), we get-
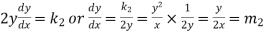 ………. (4)
………. (4)
As we know that for the condition for orthogonallity, from (2) and (4)
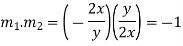
So that these two curves cut orthogonally.
Here,
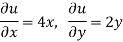
And
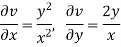
Here the C-R equation is not satisfied so that the function u + iv is not analytic.
Hence the transformation is not conformal.
Q10: How that the bilinear transformation w= 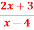 transforms
transforms 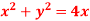 in the z-plane to 4u+3=0 in w-plane.
in the z-plane to 4u+3=0 in w-plane.
A10.
Consider 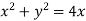 the circle in z-plane
the circle in z-plane
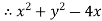 = 0
= 0

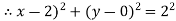
Thus, centre of the circle is (h,k) c(2,0) and radius r=2.
c(2,0) and radius r=2.
Thus in z-plane it is given as 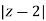 =2....(1)
=2....(1)
Consider w= 
W(z-4) = 2z+3
Wz-4w=2z+3
Wz-2z=4w+3
Z(w-2) = (4w+3)
 z =
z = 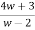
z-2 = 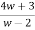 - 2
- 2