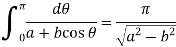Unit-5

Complex Variable –Integration

Q1: Evaluate 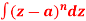where c is the circle with center a and r.

What is n = -1.

A1.

The equation of a circle C is |z - a| = r or z – a =

Where 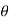varies from 0 to 2π

dz =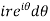

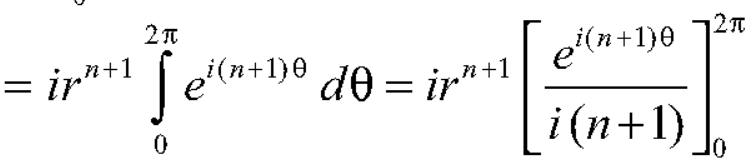
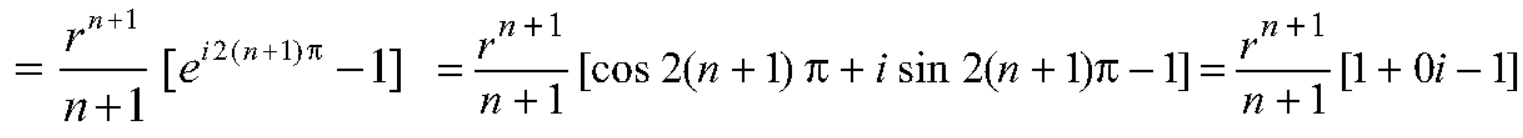
Which is the required value.

When n = -1

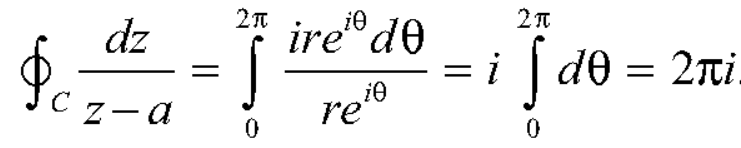
Q2: Evaluate 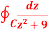where C is |z + 3i| = 2

A2.

Here we have-

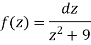
Hence the poles of f(z),

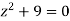
Note- put determine equal to zero to find the poles.

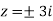
Here pole z = -3i lies in the given circle C.

So that-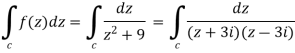
 

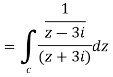
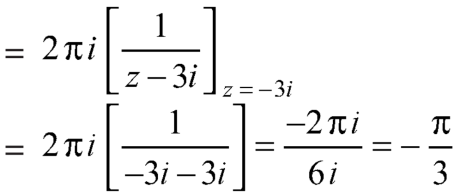
Q3: Explain the following by cauchy’s integral method:

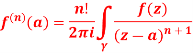
A4ution:

Given,

                  =

=

=

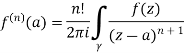
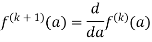
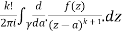
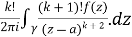
Q4: Evaluate 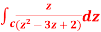by using Cauchy’s integral formula.

Here c is the circle |z - 2| = 1/2

A5. it is given that-

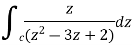
Find its poles by equating denominator equals to zero.

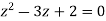
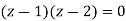
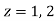
There is one pole inside the circle, z = 2,

So that-

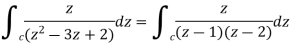
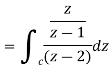
Now by using Cauchy’s integral formula, we get-

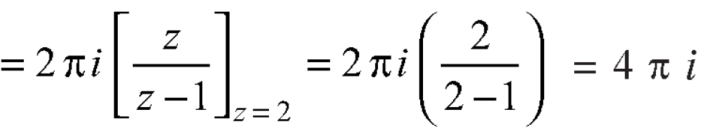
Q5: Evaluate the integral given below by using Cauchy’s integral formula-

A6. Here we have-

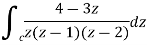
Find its poles by equating denominator equals to zero.

We get-

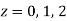
There are two poles in the circle-

Z = 0 and z = 1

So that-
 

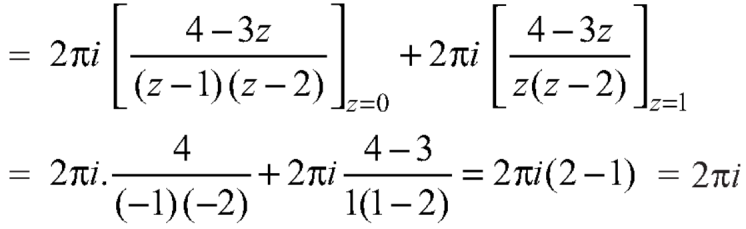
Q6: Expand sin z in a Taylor’s series about z = 0.

A7.

It is given that-

Now-

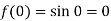
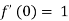
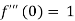
We know that, Taylor’s series-

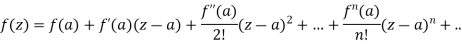
So that

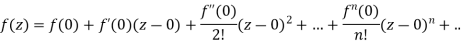
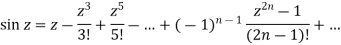
Hence

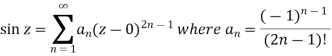
Q7: Find the Laurent’s expansion of-

In the region 1 < z + 1< 3.

A8.

Let z + 1 = u, we get-

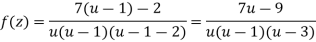
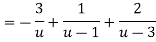
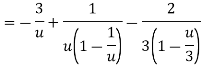
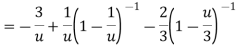
Here since 1 < u < 3 or 1/u <  1 and u/3 < 1,

Now expanding by Binomial theorem-

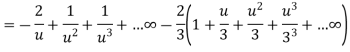
Hence

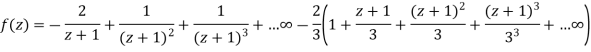
Which is valid in the region 1 < z + 1 < 3

Q8: Determine the poles of the function-

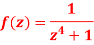
A9.

Here we have-

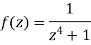
We find the poles by putting the denominator of the function equals to zero-

We get-

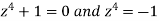
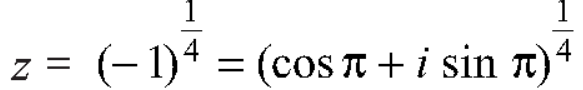
By De Moivre’s theorem-

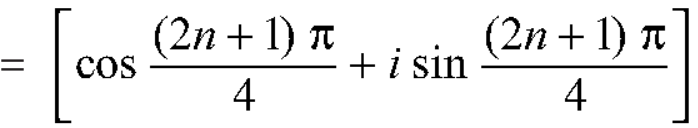
If n = 0, then pole-

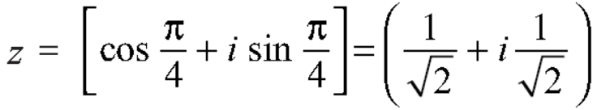
If n = 1, then pole-

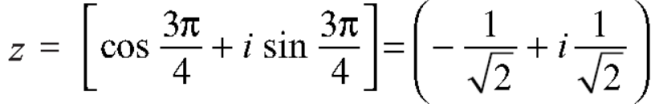
If n = 2, then pole-

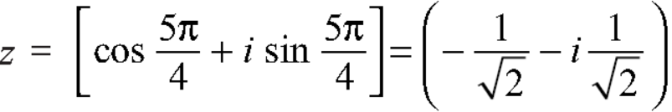
If n = 3, then pole-

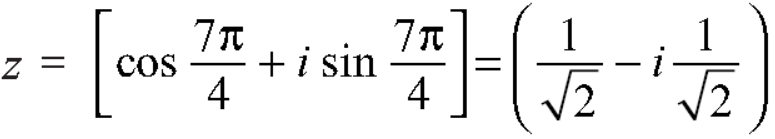
Q9: Evaluate .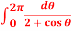

A10.

Here put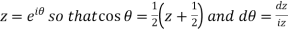

Then-

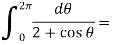
Where C is the circle |z| = 1

The pole of the integrand are the roots of 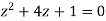which are-

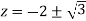
Out of the two poles, here z 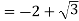 lies inside the circle C.

Residue at z 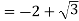 is-

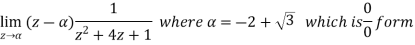
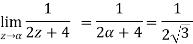
By residue theorem-

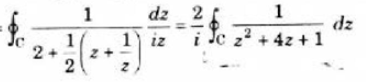
So that-

Q10: Evaluate 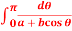where a > |b|.

A11.

As we know that-

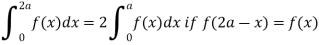
So that-

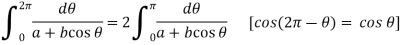
Or

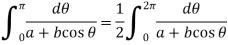
Now on putting , we have-

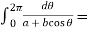
Where c is the circle |z| = 1.

Residue at z = 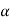is-

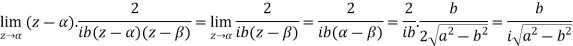
By residue theorem-

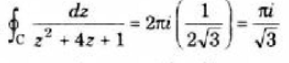
Hence-