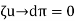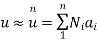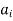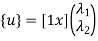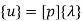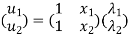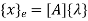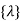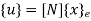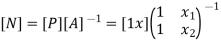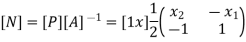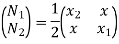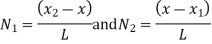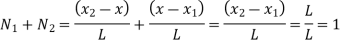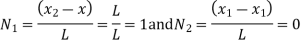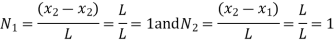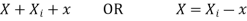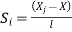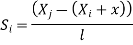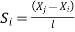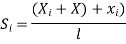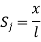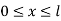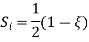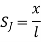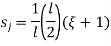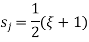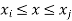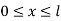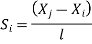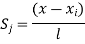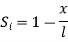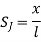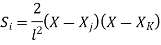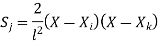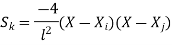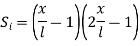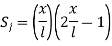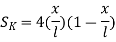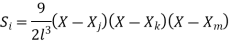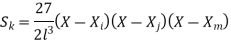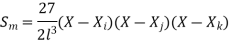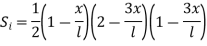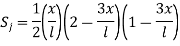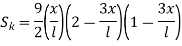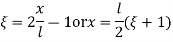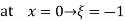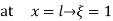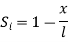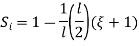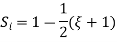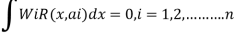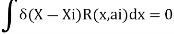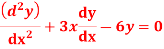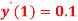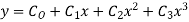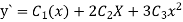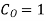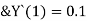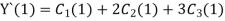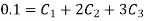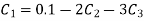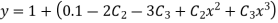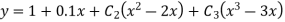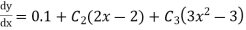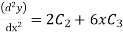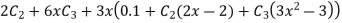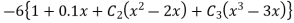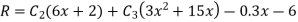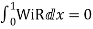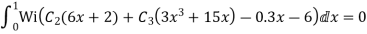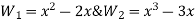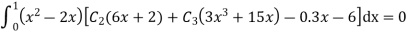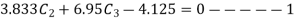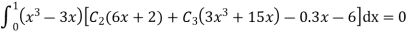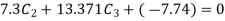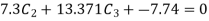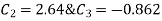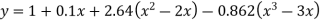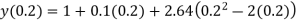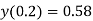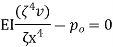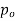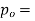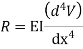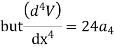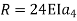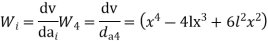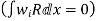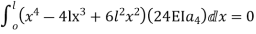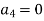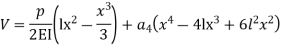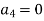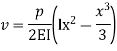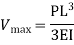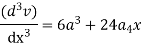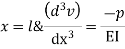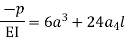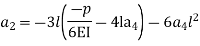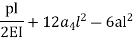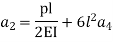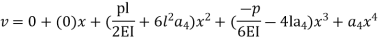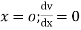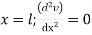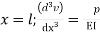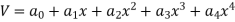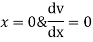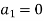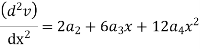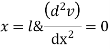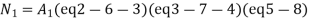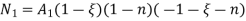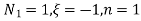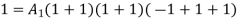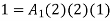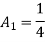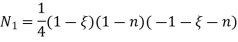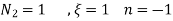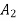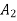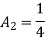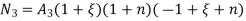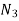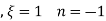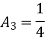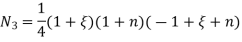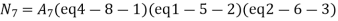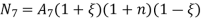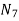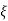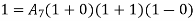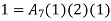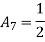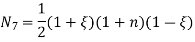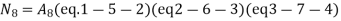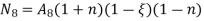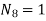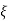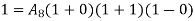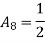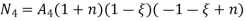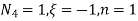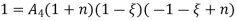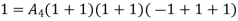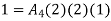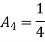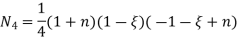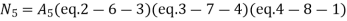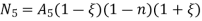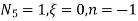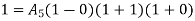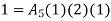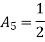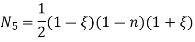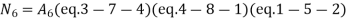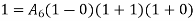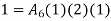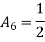|
|
Variational method- principles
U is solution to continum problem F,E are differential operators
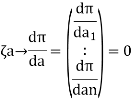
Now, u is exact solutions if for any arbitary
i.e if variational integral is made “stationary” now the approximate solution can be found by substituting trial function expansion .
since above holds true for any
parameter
|
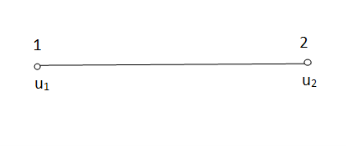
 are the certesian co-ordinaters of nodes 1&2 respectively .
are the certesian co-ordinaters of nodes 1&2 respectively . 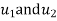 are displacement of nodes 1and 2 u is the displacement of any point in x-directions
are displacement of nodes 1and 2 u is the displacement of any point in x-directions
|
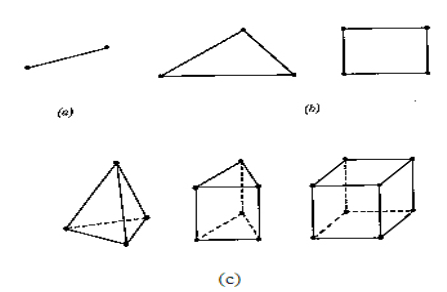
Total DOF =O2 (one 2t each node)
u=λ1+λ2x in matrix form
Where [p] =parametric matrix II. Displacement function in-terms of nodal displacement :express displacement function in terms of nodal displacement using the coordinates of nodes
Where [A] =connectivity matrix obtained
Where [N] =shape functions [N] =[p] III. shape functions =
Inverse is obtained by using method of adjoin
Sum of shape functions is always unity
At node 1 x=
At node 2, x=
|
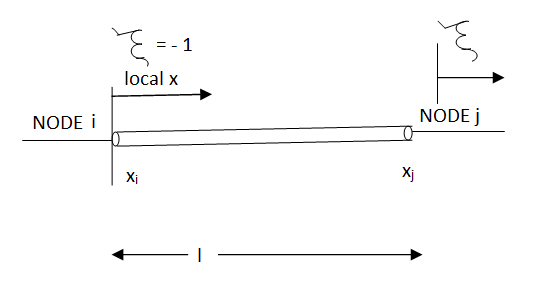
The relationship between a global coordinates X & a local coordinates x.
Linear shape functions in local ordinates
2.
Notice
|
Interpolation function | In term of global coordinates (x).
| In terms of local coordinates (x)
|
Linear |
|
|
Quadratic |
|
|
Cubic |
|
|
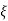 lower case
lower case 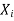
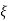 to be 1 at I & 1 at j .
to be 1 at I & 1 at j . 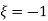
|
The relationship between local coordinates x& the natural coordinates
linear share function in natural coordinates
|
|
 in this method.
in this method.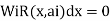
|
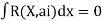
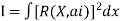
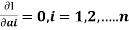
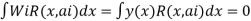
|
Step 1 :- see the order of the equation given :- if ‘n’ then assume polynomial of order/degree “n+1” Now,
step 2 – apply boundary conditions one by one i.e y(0) =1
Rewrite the approximately solution is
Step 3- find the reside given by the differential equations i.e ,
The residue becomes
Step 4 – the weighted integral from
Wi -> coefficient of Ci in y i.e from equation C
Now, putting i=1 , we get
Similarly putting i=2 , we get
On solving
Solving 1 & 2
Therefore,
|
|
|
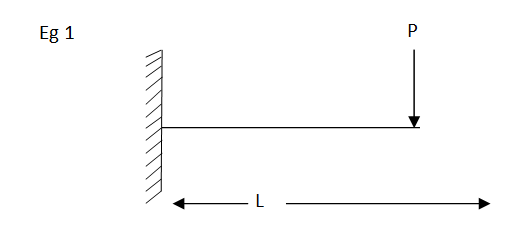
Step 1 – formulate differential equation of beam
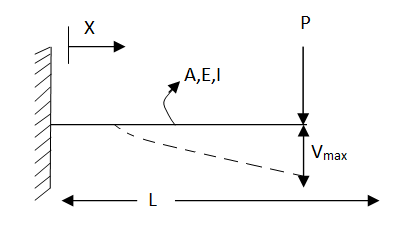
Where v= disp. In ‘y’ dim
Step -2 Residual
Weighting function
Step -3 Use galerkin’s formulation
Step – 4 find the unknown displacement
But
The maximum disp. In beam at x=l
By using 4th boundary con
This is a admissible trial solution . Step – 5 trial balance function & boundary conditions
Boundary conditions
By 1st boundary conditions
By 3rd conditions
|
|
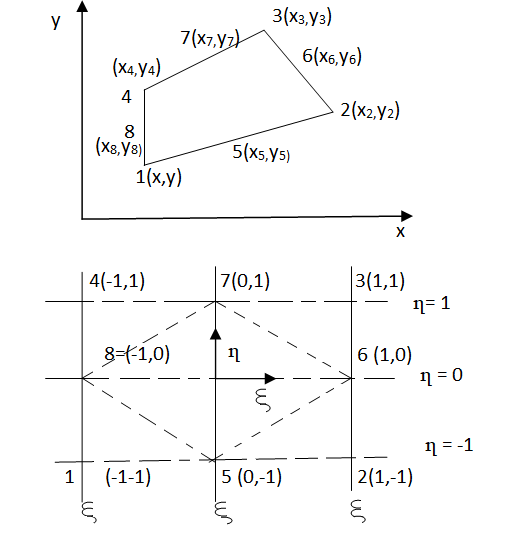
At node 1 ,
At node 2 , 1= 1=
At node 3 ,
At node 7 ,
At node 8,
at node 4,
At node 5 =
At node 6,
|