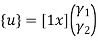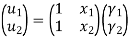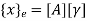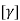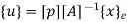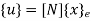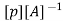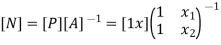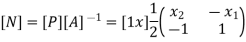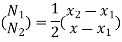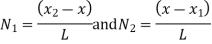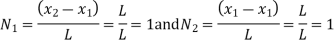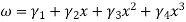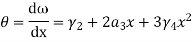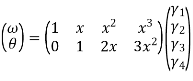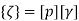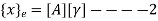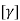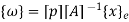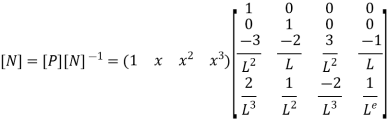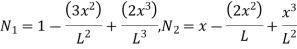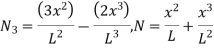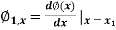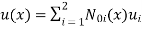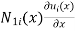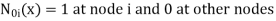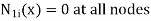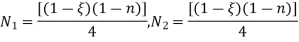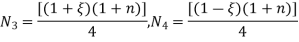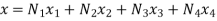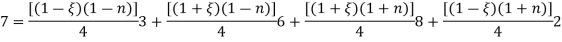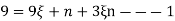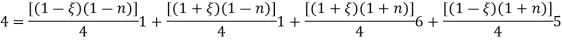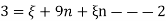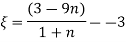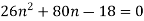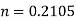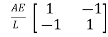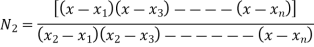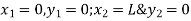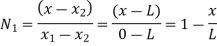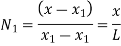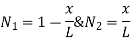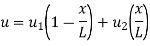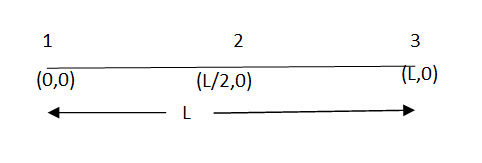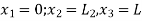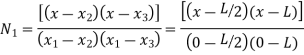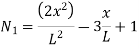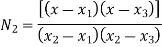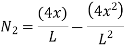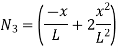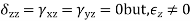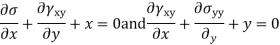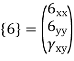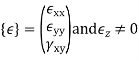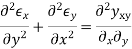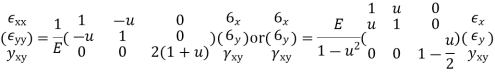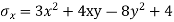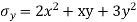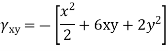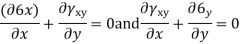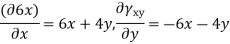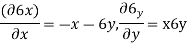|
|
|
|
|
|
|
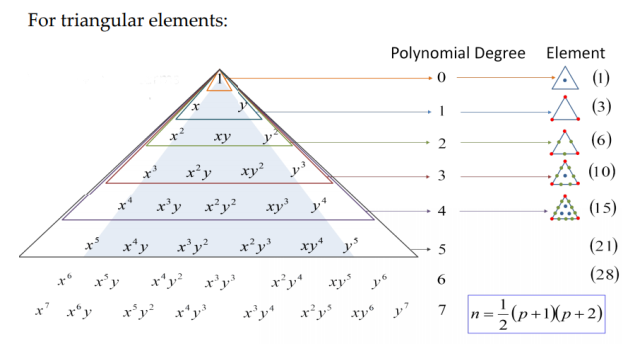
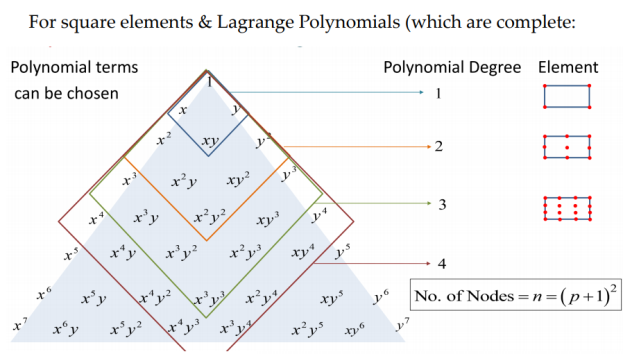
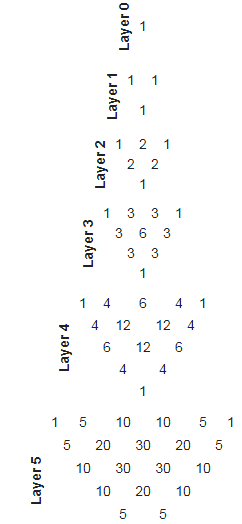
 Layer is the
Layer is the  triangular number:
triangular number: 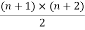
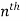 Layer is .
Layer is .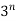
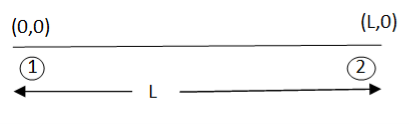
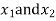 are the cartesian co-ordinates of nodes 1& 2 respectively.
are the cartesian co-ordinates of nodes 1& 2 respectively. 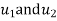 are displacement of nodes 1 and 2 u is the displacement of any point in x-directions.
are displacement of nodes 1 and 2 u is the displacement of any point in x-directions.
1 2
|
In matrix form ,
Where , [p]= parametric matrix II. Displacement function in terms of nodal displacement Express displacement function in terms of nodal displacement using the co-ordinates of nodes
Where ,[A]= connectivity matrix Obtained
Where [N]= shape function [N]= III. shape function :-
Inverse is obtained by using method of adjoin
Sum of shape functions is always unity
At node 2, x=
|
Total Dof are 04 w= translation
In matrix form
Where [p]= parametric matrix II. Displacement function in terms of nodal displacement Express displacement function in terms of nodal displacement using the coordinates of nodes x=0 at node 1 and x=L at node 2
Where [A]= connectivity matrix Obtaining We get,
Where [N]= shape function III. Shape functions
Inverse of [A] is obtained using elementary operations of matrix algebra
At node 1;x=0 N1=1 , N2=0 , N3=0 , N4=0 At node,x=L N1=0 , N2=0 , N3=1 , N4=0
|
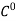 continuity. If we additionally need continuity of the first derivatives between the finite elements we use Hermition polynomials.
continuity. If we additionally need continuity of the first derivatives between the finite elements we use Hermition polynomials.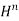 (x), is a 2n+1 order Polynomial. For example a Hermitian polynomial of the first order is actually a third order polynomial.
(x), is a 2n+1 order Polynomial. For example a Hermitian polynomial of the first order is actually a third order polynomial.
|
|
|
|
|
|
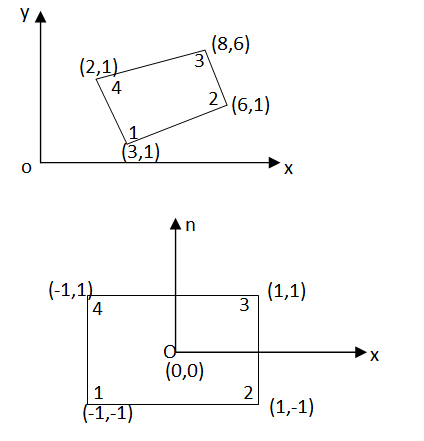
Shape functions for the four noded rectangular element in natural co-ordinates system are-
Cartesian coordinates of point ‘p’ are
Given p(x,y) =p(7,4)
From eq. 1
Put into the eq. 2
Put this value in eq. 3
|
K=
|
|
Suppose we want to find Now,
Where,
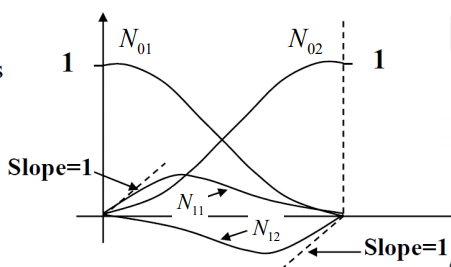
Note:- shape function has a unit value at one nodal point (for which it is calculated) & zero value at all other nodal points. Simple exercise-
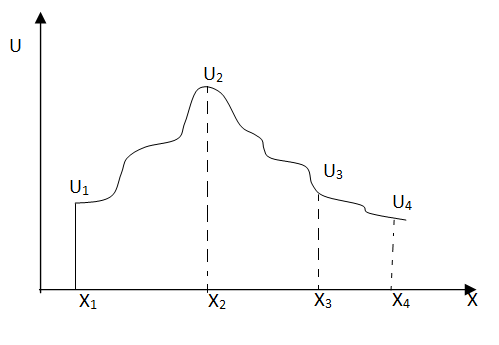
Fig.
Variation of shape function
Fig.
2. Three nodal truss element.
Fig.
Similarly
|
|
|
Equations of equilibrium
State of stress at a point
State of strain at a point
Strain -displacement relationship
Stress strain relation
Que – show that the following state of stress Ps in equilibrium
Sol- differential equation of equilibrium of 2D elasticity problem is given by
Putting these differential quantities in equations of equilibrium 1 and satisfying those. This proves that given state of stress is in equilibrium.
|