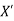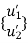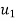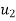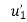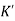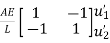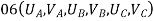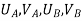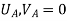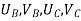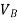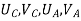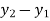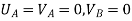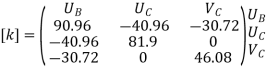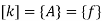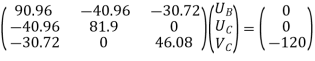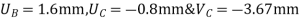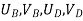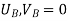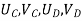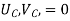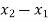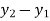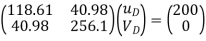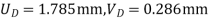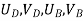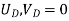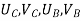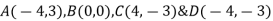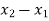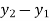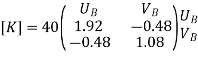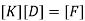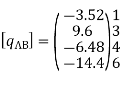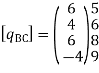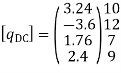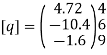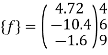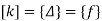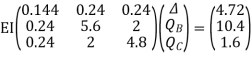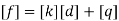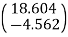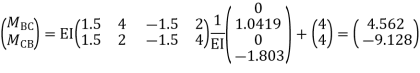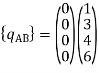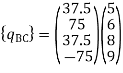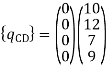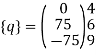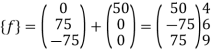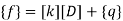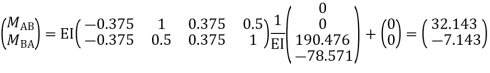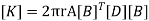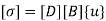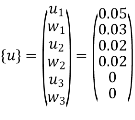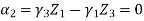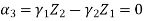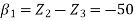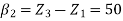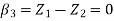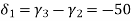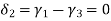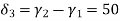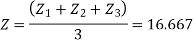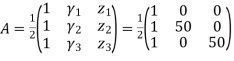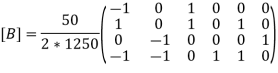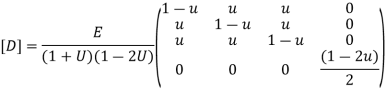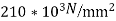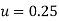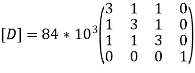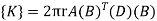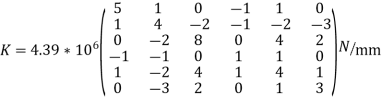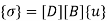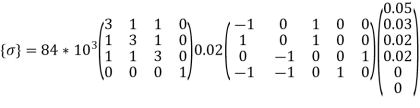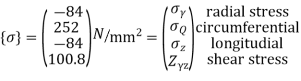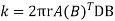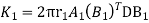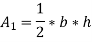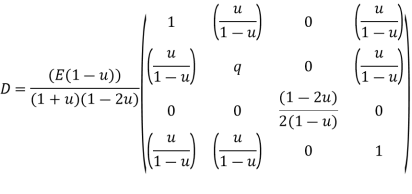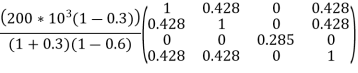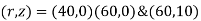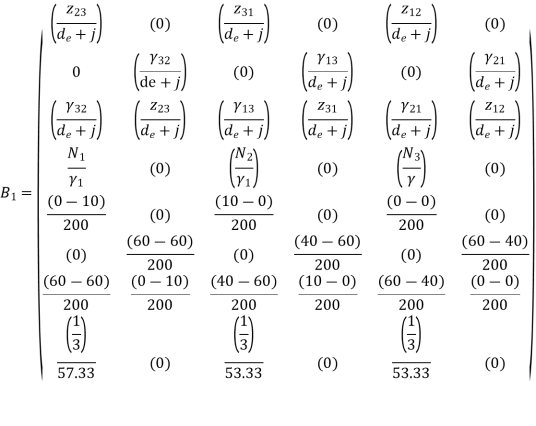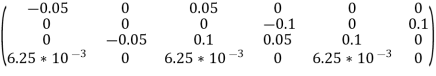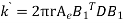undefined | unit 5 analysis of structures

FEM

Unit 5Analysis of structures Q1) Explain the Analysis of structures: Truss elements.A1)

Definition: A truss is a structure that consists of

1) All straight members2) Connected together with pin joints3) Connected only at the ends of the members4) And all external forces (loads & reactions) must be applied only at the joints.

The analysis of trusses is usually based on the following simplifying assumptions:

1) The centroidal axis of each member coincides with the line connecting the centers of the adjacent members and the members only carry axial force.2) All members are connected only at their ends by frictionless hinges in plane trusses.

Trusses Using FEA In this section, we will apply basic finite element techniques to solve general two dimensional truss problems. The technique is a little more complex than that originally used to solve truss problems, but it allows us to solve problems involving statically indeterminate structures.

Q2) Explain Analysis of truss problems by direct stiffness method.A2)Stiffness matrix of a truss element

The truss may be statically determinate or indeterminate. All members are subjected to only direct stresses (tensile or compressive). Joint displacements are selected as unknown variables.

Since there is no bending of the members we have to ensure only displacement continuity (C continuity) and there is no need to worry about slope continuity (C continuity).

Here we select two noded bar element for the formulation of stiffness matrix of truss element. Since the members are subjected to only axial forces, the displacements are only in the axial directions of the members.

Therefore, the nodal displacement vector for the bar element is

{}=

Where, and are the displacements in axial direction of the element. The stiffness matrix of a bar element is

[]=

Q3) Example -Analyze the truss as shown in fig. cross sectional area of members are AB= 1000

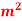, BC=800

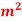,CA= 800

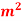take E

$C:\Users\Ssd\Desktop\Untit 5 1.png$

Fig.1 A3)

$C:\Users\Ssd\Desktop\Unit 5 2.png$

Fig.2

Step-1 degrees of freedom

Discretization –

Elements	Nodes	Displacements mm	Boundary conditions
1	AB
2	BC		=0
3	CA		-

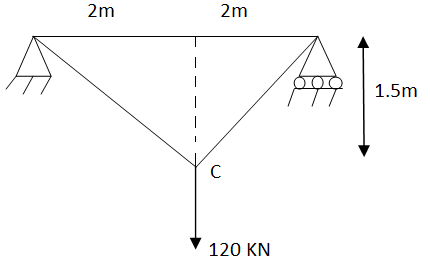
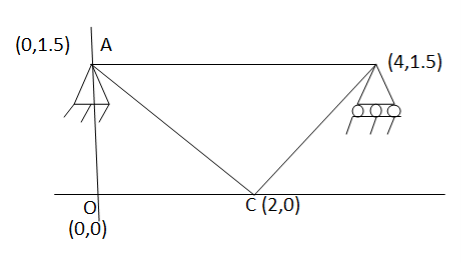
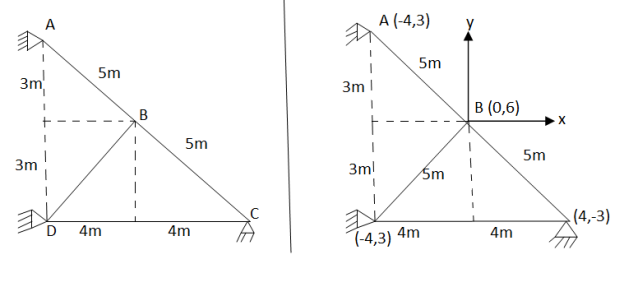
Assume x-axis horizontal through point (& vertical through point A). the co-ordinates of node A(0,1.5) , B(4,1.5) & C(2,0) . take E in Gpa.

Member			L	l	m	AE/l (KN/mm)
AB	4	0	4	1	0	50
BC	-2	-1.5	2.5	-0.8	-0.6	64
CA	-2	1.5	2.5	-0.8	0.6	64

Step-2 element stiffness matrices

Stiffness matrix of element AB .

Stiffness matrix of element BC

Stiffness matrix of element CA

Step 3- global stiffness matrix

Total Dof are 06, size of stiffness matrix 6*6

Step -4 reduced stiffness matrix

Since eliminate corresponding rows & columns from global stiffness matrix

Step -5 equation of equilibrium

Q4) Example -Figure shows a plane , truss with three members cross- sectional area of all members 500

young modulus is 200 KN/

. Determine deflection at loaded joint.

S4)

Step 1 – degree of freedom ;-

Discretization

Element	Nodes	Displacement (mm)	Boundary cond
1	AD
2	BD
3	CD

Assume origin support A(0,0). The co-ordinates of other nodes& B(1000,0), C(2000,0) and D(1500,1000)

Member			L	l	m	AE/L (KN/M)
AD	1500	1000	1802.8	0.832	0.555	88.75
BD	500	1000	1118	0.447	0.894	143.112
CD	-500	1000	1118	-0.477	0.894	143.112

Step -2 element stiffness matrices

Stiffness matrix of element AD

Step – 4 equations of equilibrium

Q5) Example – For the truss as shown in fig. using finite element method, determines deflections at loaded joints. The joint B is subjected to 50 KN horizontal force towards left & 80 KN force vertically downward. take cross sectional area of all the members 1000

young modulus is 200 Gpa.

$C:\Users\Ssd\Desktop\UNIT 5 4.png$

Fig.4A5)

Step -1 degree of freedom (06)

Discretization

Element	Nodes	Displacement (mm)	Boundary cond
1	AB
2	DB
3	CB

Assume origin point B. the co-ordinates points are

Members			L	l	m	AE/L (kN/mm)
AB	4000	-3000	5000	0.8	-0.6	40
DB	4000	3000	5000	0.8	0.6	40
CB	-4000	30000	5000	-0.8	0.6	40

Step -2 stiffness matrix of element AB .

Stiffness matrix at element DB.

Step 3- reduced stiffness matrix

Step 4- equation of equilibrium

Q6) Explain Steps for the solution of Indeterminate plane frames using finite element method.A6)Steps for the solution of Indeterminate plane frames using finite element method:1. Divide the frame into number of elements (Take one member as one element)2. Identify total degrees of freedom (Three D.O.F. at each node, two displacements and rotation)3. Determine stiffness matrices of all elements ([K]1, [K]2……)4. Assemble the global stiffness matrix [K] 5. Impose the boundary conditions and determine reduced stiffness matrix.6. Determine element nodal load vector [q] (Restrained structure)7. Determine equivalent load vector[f]8. Apply equation of equilibrium [K]{∆}={f}, and determine unknown joint displacements.9. Apply equation [K]{∆}+[q]={f} to determine reactions and moments Q7) Example - Analysis the portal frame as shown in fig. using finite element methos take EI constant. Neglect axial deformation

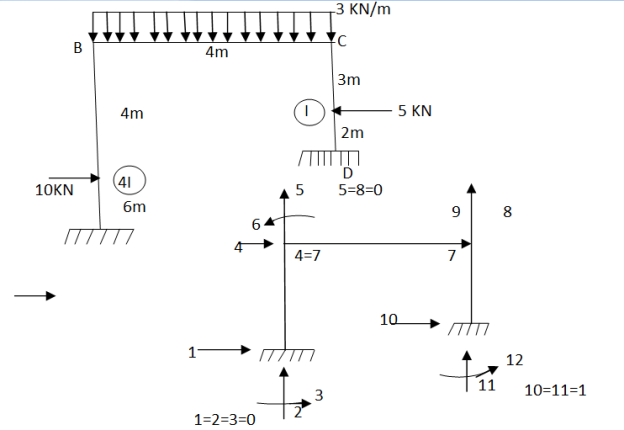
$C:\Users\Ssd\Desktop\UnIT 5 5.png$

Fig.5 Solution-

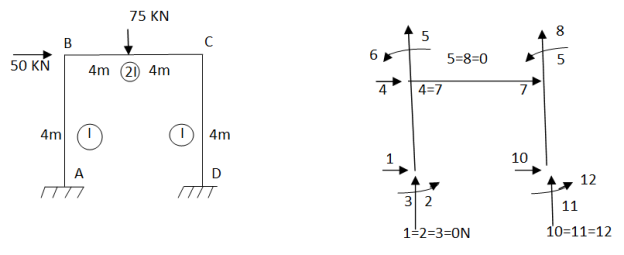
Step -1 total DoF =12

(three DOf at each node, two displacement & one rotation)

No. of elements 03 (AB,BC,CD)

Discretization

Element	Nodes	Displacement	Boundary conditions
1	AB	1,2,3,4,5,,6,	1=2=3=zero
2	BC	4,5,6,7,8,9	5=8=zero,4=7
3	DC	10,11,12,7,8,9	10=11=12=zero

Step 2- element stiffness matrix

Element stiffness matrix from AB (column member)

Imposing boundary conditions 5=8=0

Element stiffness matrix for DC

Imposing boundary conditions 10=12=0

Step -3 reduced stiffness matrix

Since horizontal sway at B& C are same (4=7) we can modify the above stiffness matrix as

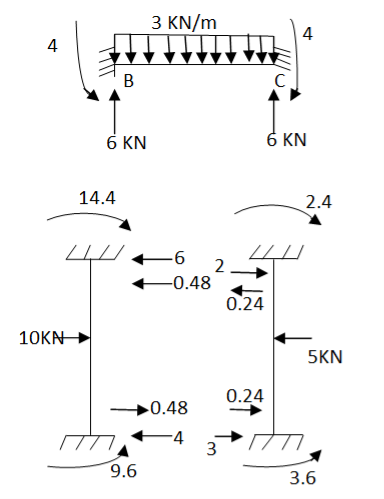
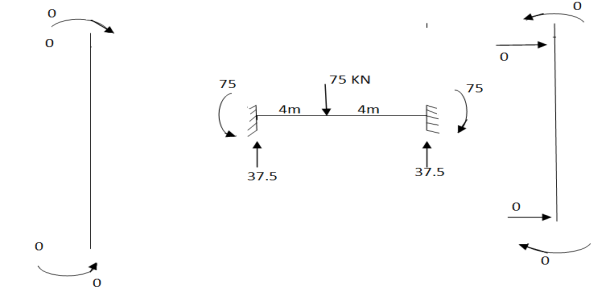
Step -4 element nodal load vector

$C:\Users\Ssd\Desktop\UnIT 5 6.png$

Fig.6

Reduced element nodal load vector

Step -5 equivalent load vector

{f}= {q}+ joint forces

Step -6 equation of equilibrium

Step -7 moment calculations

Member AB

Member BC

Member DC

Q8)Example – Analyze the rigid frame by using finite element method. Take EI constant . neglect axial deformation

$C:\Users\Ssd\Desktop\UNIT 5 7.png$

Fig.7 A8)

Step -1 total DOf =12

(three dof at each node , two displacements & one rotation)

Element	Nodes	Displacement	Boundary conditions
1	AB	1,2,3,4,5,,6,	1=2=3=zero
2	BC	4,5,6,7,8,9	5=8=zero,4=7
3	DC	10,11,12,7,8,9	10=11=12=zero

Step -2 element stiffness matrix for column AB

Element stiffness matrix of beam Bc

Element stiffnes matrix of beam DC.

Imposing boundary condition

1=2=3=5=8=10=11=12=0

Step -3 reduced stiffness matrix

Since horizontal sway at B &C are same (4=7) , we can modify the above stiffness matrix as

Step -4 element nodal load vector

$C:\Users\Ssd\Desktop\UnIT 5 8.png$

Fig.8

Reduced element nodal load vector

Step -5 equivalent load vector

Step -6 equation of equilibrium

Step -7 moment calculations

Member AB

Member BC

Member DC

Q9) Example For the axisymmetric element shown in figure, determine the element stresses Let E=210

$C:\Users\Ssd\Desktop\UnIT 5 9.png$

Fig.9 Poisson’s Ratio=0.25The total displacements are u1=0.05mm ; W1=0.03mmu2=0.02mm; W2=0.02mmu3=0mm;W3=0mm To Find Element Stresses & Stiffness Matrix

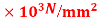
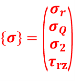S9)

We know that

=1250mm

Substitute all this values in {B}

Put =E =

We know that stiffness matrix

Note ; matrix form [k]= (6*6)

To find stresses

Note – matrix form = 4*1

Q10) Example :- A long hollow cylinder of inside diameter 80mm & outside diameter 120mm is firmly filled in a hole of another rigid cylinder over it full length as shown in fig. the cylinder is then subjected to an internal pressure of 2 MPa. By using two elements on the 10mm length shown . find the displacement at the inner radius . take E=200 Gpa ,u=0.3

$C:\Users\Ssd\Desktop\UNIT 5 10.png$

Fig 10 S10)

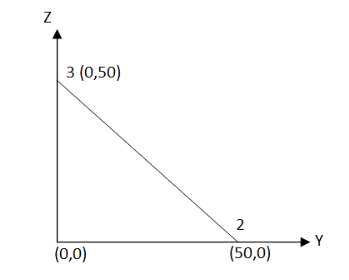
Stiffness matrix for element 1

For the both elements

The stiffness matrices for element

Sign Up