Unit 1 | unit 1 fluid and continuum

Back to Study material

Unit - 1

Fluid and Continuum

Q1) Explain the classification of fluid?

A1)

There are two types of fluids:

Liquid and Gases
Ideal fluid and Real Fluid

1. Liquid and Gases

Liquid:

Fluids, which are not able to compress, but possess a deficit volume, which are not affected appreciably by the change in pressure and temperature is called as liquid. e.g., Water, Kerosene, Petrol etc.
A liquid being composed of relatively closed-packed molecules with strong cohesive forces tends to retain its volume and will form a free surface in gravitational field or in container as shown in Fig.

Gases:

A fluid which are compressible and possess no definite volume, it is compressed or expands at any change in temperature is called as gases. e.g., Air, Ammonia, CO, etc.
Gas molecules are widely spaced with negligible cohesive forces, so that it is free to expand until it encounters confining walls as shown in Fig.

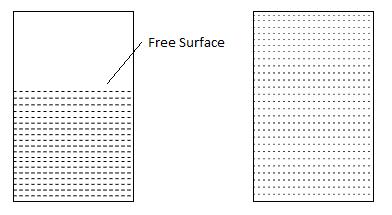
Fig.: Liquid and Gases resp.

2. Ideal fluid and Real Fluid:

Ideal fluid-

Fluids which have no viscosity and surface tension and those are incompressible is called as ideal fluid. Ideal fluids are an imaginary fluid and do not exist in the nature.
As water is incompressible, it is considered as an ideal fluid.

Real fluid-

Fluids which possess the properties like viscosity, surface tension and compressibility is called as real or practical fluid.
Whenever the motion takes place, the tangential or shears force is always offered by the fluid.

Q2) Explain the application of Fluid Mechanics?

A2)

The application of fluid mechanics are as follows:

The flight of birds in the air and the motion of the fish in the water are governed by the law of fluid mechanics.
The cricket ball bowling depends upon circulation principle to provide the ball with desired spin and flight.
The circulation of blood in veins and arteries follows the law of fluid resistance.
The design of aeroplanes and ships are based on the theory of aerodynamics and buoyancy.
The oil and gas pipelines, the water supply systems are designed on the principles of fluid mechanics.

Q3) What is Continuum?

A3)

A continuous distribution of matter with no voids or empty spaces is called as continuum. For mechanical analysis, a fluid is considered to be continuum. e.g., water flowing through pipes, channel.
Continuum is based on assumption that fluid is continuous. That is the properties such as density, pressure, temperature and velocity are taken to be well defined at infinitely small points and are assumed to vary continuously from one point to another. Air is considered as a Continuum.
The mean-free-path-of atmospheric air is about 5 - 7.5 x 10-6 cm but this molecular spacing increases even under lower pressure, and the air no longer remains a continuum.

Q4) What are the physical properties of fluid?

A4)

Physical properties of fluid are as follows:

Density or Mass Density
Weight Density or Specific Weight or Unit Density
Specific Volume
Specific Gravity or Relative Density

1.Density or Mass Density:

The density of a fluid is defined as the mass per unit volume.
It is denoted by 'p' (rho). S.I. Unit is kg/m³.
Mass density of water is 1000kg/m³.

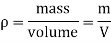
2.Weight Density or Specific Weight or Unit Density:

The specific weight of a fluid is defined as weight per unit volume at a standard temperature and pressure.
It is denoted by 'w' or 'y' (gamma). It has S.1. Unit is N/m. Specific weight of water is 9810 Nin (9.81 kN/m).

∴

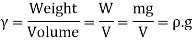
The specific weight depends on gravitational acceleration and the mass density. Since gravitational attraction varies from place to place, the specific weight will also vary.

3. Specific Volume

Specific volume of a liquid is the volume of the fluid per unit weight. It is the reciprocal of specific weight.
It is denoted by 'V'. S.I. Unit is m3/N.

Vs=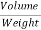==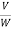 in case of liquid

For the gas flow, specific volume is defined as the volume of the fluid per unit mass. In this case it is a reciprocal of mass density. S.I. Unit is m3/kg.

Vs=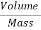== in case of gas

4. Specific Gravity or Relative Density

Specific gravity is the ratio of specific weight (or mass density) of fluid to the specific weight (or mass density) of a standard fluid.
It is denoted by S or RD.
Specific gravity =
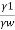
For liquid, water and for gases, hydrogen or air is consider as a standard fluid.
Specific gravity of water at a standard temperature 4°C is 1 and that of mercury is 13.6.

Q5) Explain U-tube Manometer?

A5)

Piezometer cannot be employed when large pressures in the lighter liquids are to be measured, since this would require very long tubes, which cannot be handled conveniently.
Furthermore, gas pressures cannot be measured by piezometer because a gas forms no free atmospheric surface.
These limitations can be overcome by the use of U-tube manometers.
A U-tube manometer consists of a glass tube but in U-shape, one end of which is connected to a point at which pressure is to be measured and other end remains open to the atmosphere as shown in fig.

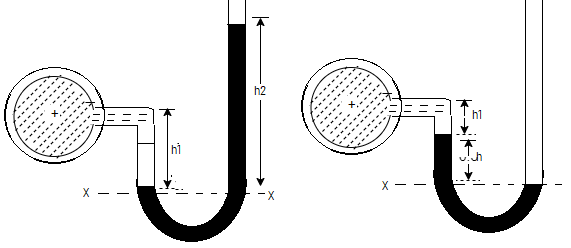
Fig.: U-tube manometer

Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)

Let, h1 = height of the light liquid in the left limb above the datum line

h2 = height of the heavy liquid in the right limb above the datum line

h = pressure in pipe, expressed in terms of head

S1 = specific gravity of the light liquid, and

S2 = specific gravity of the heavy liquid

The pressure in the left limb and right limb above the datum line X-X are equal.

Pressure head above X-X line in the left limb = h+h1S1

Pressure head above X-X in the right limb = h2S2

Equating these two pressures, we get

For negative pressure:

Refer to fig(b)

Pressure head above x-x in the left limb=

Pressure head above x-x in the right limb = 0

Equating these two pressures, we get

h + h1S1 + h2S2 = 0 or h = - h2S2 - h1S1

Q6) A simple U-tube manometer is used to measure water pressure in pipe line. The left limb of manometer connected to the pipe and the night limb is open to atmosphere. The mercury level in the left limb is 80mm below the center of the pipe and the level in the right limb in 220mm above the center of the pipe. Calculate the pressure of water in meter and also in km

A6)

Oil

Mercury

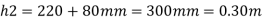
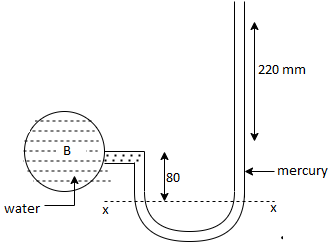
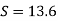
Pressure in the left limb about xx = Pressure in the right limb about x-s

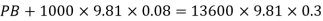
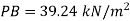
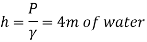
Q7) A U-tube manometer is used to measure the pressure of water in a pipe line, which is in excess of atmospheric pressure. The night limb of the manometer contains mercury and is open to atmosphere. The contact between water and mercury is in the left limb. Determine the pressure of water in the main line, if the difference in level of mercury in the limbs of U-tule 12 cm and the free surface of mercury is in level with the centre of the pipe. It the pressure of water in pipe he is reduced to 9810 N/m². Calculate the new difference in the level of mercury.

A7)

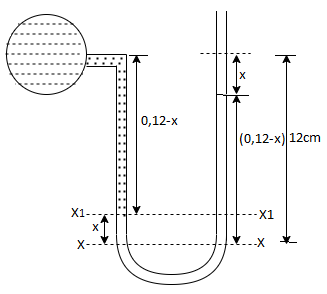
Case I:

Given:

h1, =h₂= 12cm=0.12 m.

S2=13.6

Pressure in pipe

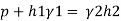
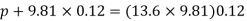
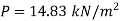
Case II:

Since the pressure in the pipe is reduced to 9.81 kN/m² (which is less than 14.83 kN/m²), the mercury in the left limp will be rise. Rise of mercury in the left limb will be equal to the fall of mercury in right limb as the total volume of mercury remains same.

Let x = rise of mercury in left limb= fall in mercury in right limb,

Pressure at new section x₁ - x₁

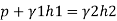
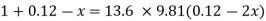
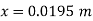
New difference of mercury

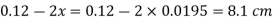
Q8) Fig. P shows a conical vessel having its outlet at A to which a U-tube manometer is connected. The reading of the manometer given in the Fig. P. 3.7.15 shows when the vessel is empty. Find the reading of the manometer when the vessel is completely filled with water.

A8)

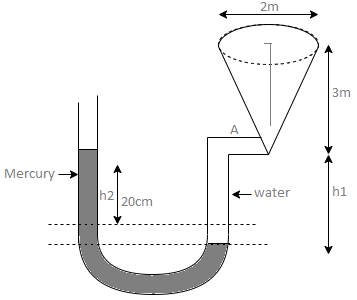
Case I:

Vessel is empty

Pressure in left limb about x-x= Pressure in right limb about x-x

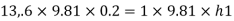
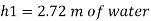
Case II: Vessel is full of water

When pressure is full of water, the pressure in right limb will increase and mercury level will fall by 'y' m, similarly Hg level in left limb will rise by 'y' m

Now consider 7-7 as a datum

Pressure in left limb = Pressure in right limb about z-z

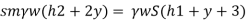
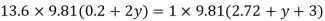
:. Difference of mercury level when the vessel is full of

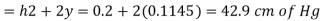
Q9) Explain U-Tube Differential Manometer?

A9)

A U-tube differential manometer is shown in fig.

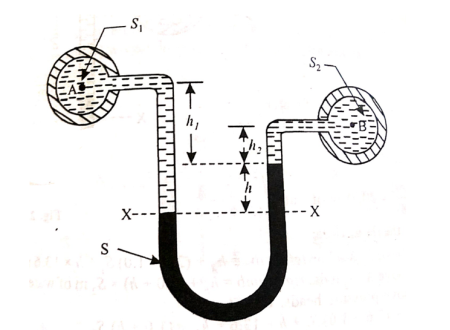
Fig.: U tube differential manometer

Let, h = difference of mercury level (heavy liquid) in the U-tube,

h1 = distance of the centre of A, from the mercury level in the left limb

h2 = distance of the centre of B, from the mercury level in the right limb,

S1 = specific gravity of liquid in pipe A,

S2 = specific gravity of liquid in pipe B,

S = specific gravity of heavy liquid o mercury

HA = pressure head at A,

HB = pressure head at B

Considering the pressure heads above the datum line x-x, we get

Pressure head in the left limb:

h A + (h 1 + h) S1

Pressure head in the right limb:

h B + h 2 × S 2 + h × S

Equating the above pressure heads, we get

h A + (h1 + h) S1 = h B + h 2 × S 2 + h× S

(h A - h B) = h 2 × S 2 + h × S - (h 1 + h) S 1

Q10) A differential manometer is connected at two points A and B of two pipes as shown in Fig. Pipe A contains liquid of specific gravity 1.6, while pipe B contains liquid of specific gravity 0.8. If the pressure at A and B are 11.80 x 10 N/m² and 19.60 x 10 N/m2, find the difference in mercury level in the differential manometer.

A10)

Pipe A

S₁ = 1.6

PA = 11.8 x 10' N/m² = 118 kN/m² 19.62× 10¹ N/m² = 196.2 kN/m²

h₁ = (2+1,5) = 3.5 h₂ = (1.5 + h)

Pipe B

s2= 0.8

h2= 1.5+h

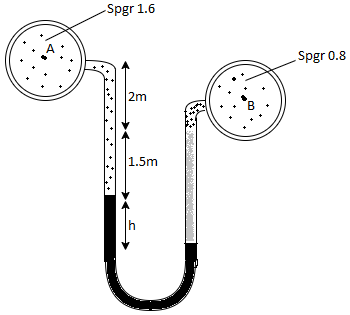
Pressure in left limb = pressure in right limb PA

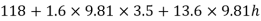
Q11) A U-tube manometer (Fig. P.) measures the pressure difference between two points A and B in a liquid of density PL The U tube contains mercury of density pa. Calculate the difference of pressure between points A and B in a liquid of density p, The u tube contains mercury of density P Calculate the difference of pressure between points A and B if the liquid contain at A is water take a 1.5 m, b=0.75 m and h= 0.50 m.

A11)

Given:

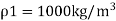
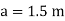
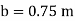
To find:

PA-PB

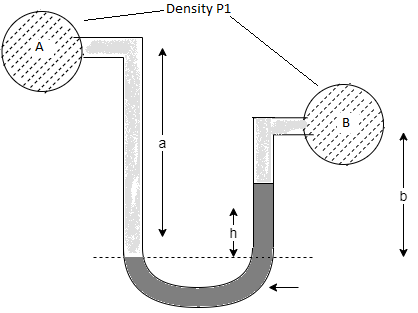
Pressure in left limb = Pressure in right limb

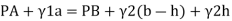
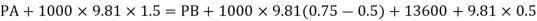
Q12) Liquid of specific gravity 1.0 flows through pipes A and B at positive pressures of 0.5 bar and 0.25 bar respectively. Pipe A is 1.8 m higher than B. What would be the difference in the levels of U-tube manometer connected to A and B, having manometric liquid of specific gravity 13.6? Liquid level in the limb attached to A is lower than that in the order.

A12)

Given:

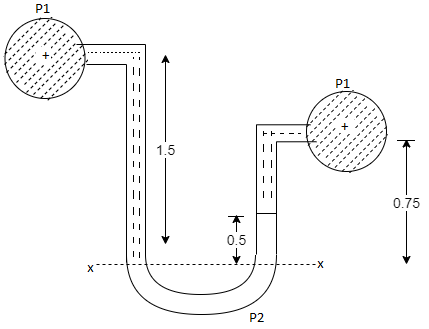
1 1bar = 10^5 N/m²,

2 P=0.5 bar = 50 kN/m².

3 pB= 0.25 bar 25 kN/m²

Balancing the liquid about x-x in left limb and right limb

Pressure in left limb about x-x= Pressure in right limb about x-x

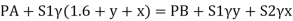
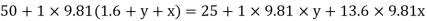
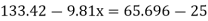
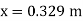
Q13) What is Micromanometer?

A13)

A micro manometer can be used - if required in combination with pitot tubes - to measure, measure, measure and calculate velocity and volumetric flow rate. Micro manometers have high accuracy for measuring high-, low- and variability. Observatory Instruments offer different micro manometers, each with a different application.

One leg of the micro manometer is the source and the other is the inclined tube, which contains a magnifier. The meniscus in the inclined tube is located at a reliable level adjusted by the hairline viewed by the magnifier.

First of all, both the source and the amplifier are the same pressure. The application of pressure at the end of the spring removes the hairline but can be restored to its original position by increasing or lowering the source (mercury sump).

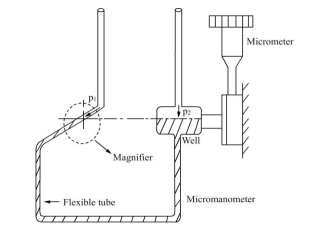
Fig.: Micromanometer

Q14) Explain Pressure on Plane and Curved Surface?

A14)

Pressure on Plane surface:

A pressure diagram is the graphical representation of the variation in the intensity of pressure over a surface. It is used to calculate total pressure force and centre of pressure for submerged body.

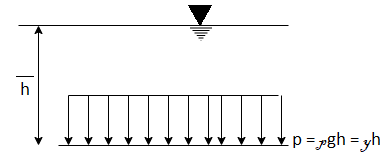
Fig.: Pressure diagram for horizontal surface

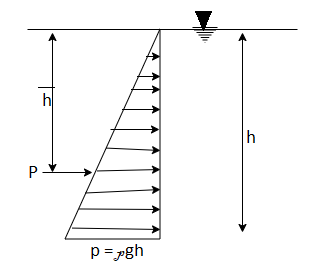
Fig.: Pressure diagram for vertical surface

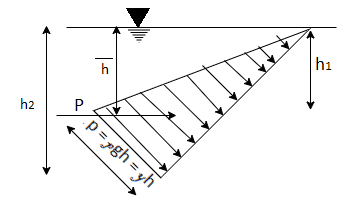
Fig.: Pressure diagram for inclined surface

Centre of pressure by principle of moment,

P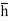=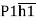+P2+P3

Pressure on Curved Surface:

Consider a completely submerged curve surface under water. Consider an elementary area dA situated at a depth 'h' below free water surface. As shown in Fig.

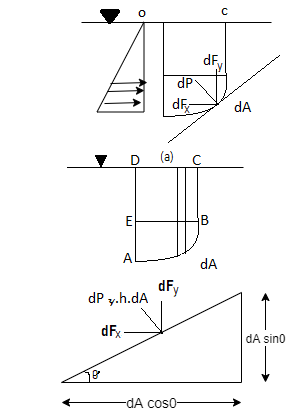
Total pressure acting on elementary area (dA)

DP = 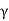hdA

Total pressure,

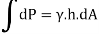
Total Pressure,

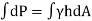∴P=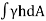

But in case of curved surface, the direction of the total pressure on the elementary area is not in the same direction, but varies from point to point. Thus, the integration of Equation for curved surface is impossible. So that this problem will be solve by resolving the force P into horizontal and vertical components PH and Py

Then total force on the curved surface is,

P =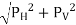

Direction of Resultant force,

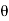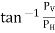
Horizontal Component,

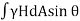∴= The total pressure force on the projected area of the curved surface on the vertical plane.

∴PH = The total pressure force on the projected area of the curved surface on the vertical plane.

Vertical components,

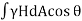∴= Vertical projected area of the curve surface as shown in Fig

∴Now dA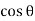= Horizontal projected area of the curve surface as shown in Fig.

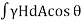∴= Total volume of liquid contained between curved surface and free surface.

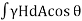∴= = Total weight of liquid contained between curved surface and free surface.

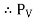= Total weight of liquid contained between curved surface and free surface.

Q15) What is Buoyancy?

A15)

The tendency of fluid to uplift a submerged body, due to the upward thrust of the fluid is known as buoyancy or force of buoyancy.
It is always equal to the weight of fluid displaced by the body.

Centre of Buoyancy:

The point at which the force of buoyancy is act is called as centre of buoyancy.
It always lies C.G. Of the volume of the liquid displaced.

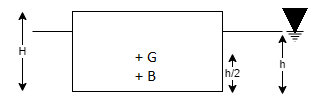
Fig.: Center of Buoyancy

Where, H is the height of body. h is submerged height of block i.e., depth of immersion.

Q16) Explain Stability of Floating bodies?

A16)

Stability of floating bodies is as follows:

(1) Stable equilibrium

When a body is given a smaller angular displacement due to external force and then it comes to its original position due to internal forces, is called as stable equilibrium.
In stable equilibrium, metacentre is lies above centre of gravity, the metacentric height is positive.
External couple is balanced by couple due to internal force.

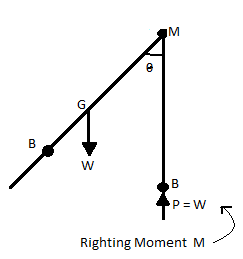
Fig.: Stable equilibrium

(2) Unstable equilibrium

When a body does not return to its original position from the slightly displaced angular position and heels farther away, is callesi.us unstable equilibrium.
In unstable equilibrium, metacentre M is lies below the centre of gravity G, the metacentre height is negative.
External couple and couple due to internal force are in same direction. It is an unstable condition.

Fig.: Unstable equilibrium

(3) Neutral equilibrium

When a body is given a smaller angular displacement and set on new position, is called as neutral equilibrium.
In neutral equilibrium, metacentre M and centre of gravity G are coincided.

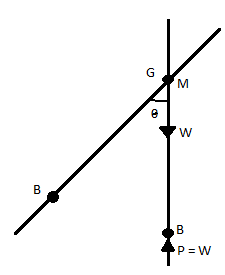
Fig.: Neutral equilibrium

Sign Up