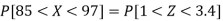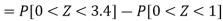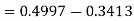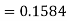Unit 4
Statistical techniques-2
Question-1: Define probability & expected value.
Solution.
Suppose there are ‘n’ exhaustive cases in a random experiment that is equally likely and mutually exclusive.
Let ‘m’ cases are favourable for the happening of an event A, then the probability of happening event A can be defined as-

The probability of non-happening of the event A is defined as-
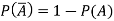
Note- Always remember that the probability of any events lies between 0 and 1.

Expected value-
Let 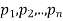 are the probabilities of events and
are the probabilities of events and 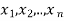 respectively. Then the expected value can be defined as-
respectively. Then the expected value can be defined as-
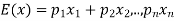
Question-2: A box contains 4 white and 2 black balls and a second box contains three balls of each colour. Now a bag is selected at random and a ball is drawn randomly from the chosen box. Then what will be the probability that the ball is white?
Solution.
Here we have two mutually exclusive cases-
1. The first bag is chosen
2. The second bag is chosen
The chance of choosing the first bag is 1/2. And if this bag is chosen then the probability of drawing a white ball is 4/6.
So that the probability of drawing a white ball from the first bag is-
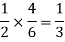
And the probability of drawing a white ball from the second bag is-

Here the events are mutually exclusive, then the required probability is-
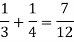
Question-3: A bag contains 9 balls, two of which are red three blue, and four black.
Three balls are drawn randomly. What is the probability that-
1. The three balls are of different colours
2. The three balls are of the same colours.
Solution.
1. Three balls will be of a different colour if one ball is red, one blue and one black ball are drawn-
Then the probability will be-
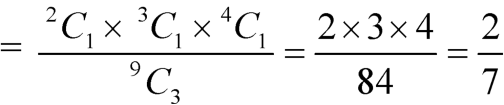
2. Three balls will be of the same colour if one ball is red, one blue and one black ball are drawn-
Then the probability will be-
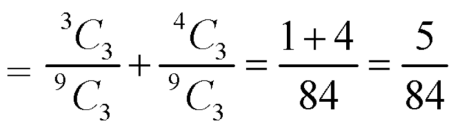
Question-4: Two male and female candidates appear in an interview for two positions in the same post. The probability that the male candidate is selected is 1/7 and the female candidate selected is 1/5.
What is the probability that-
1. Both of them will be selected
2. Only one of them will be selected
3. None of them will be selected.
Solution.
Here, P (male’s selection) = 1/7
And
P (female’s selection) = 1/5
Then-
1.

2.


3.

Question-5: A can hit a target 3 times in 5 shots, B 2 times in 5 shots, and C 3 times in 4 shots. All of them fire one shot each simultaneously at the target.
What is the probability that-
1. Two shots hit
2. At least two shots hit
Solution.

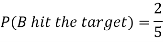
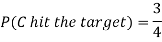
1. Now probability that 2 shots hit the target-
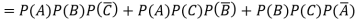
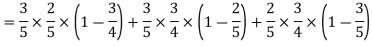
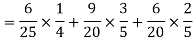
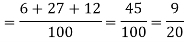
2.
Probability of at least two shots hitting the target
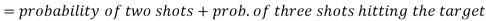
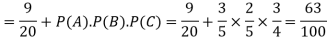
Question-6: A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.
Solution.
We consider the following events:
A: Selected item comes from A.
B: Selected item comes from B.
D: Selected item is defective.
We are looking for a 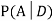 . We know:
. We know:
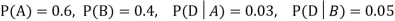
Now,
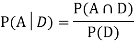
So we need

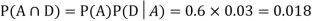
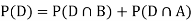
Since D is the union of the mutually exclusive events 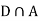 and
and 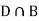 (the entire sample space is the union of the mutually exclusive events A and B)
(the entire sample space is the union of the mutually exclusive events A and B)
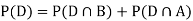
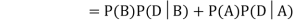
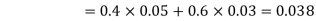

Question-7: Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball is drawn is red find the probability that it is drawn from the first urn.
Solution:
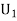 : The ball is drawn from urn I.
: The ball is drawn from urn I.
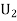 : The ball is drawn from urn II.
: The ball is drawn from urn II.
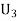 : The ball is drawn from urn III.
: The ball is drawn from urn III.
R: The ball is red.
We have to find 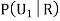
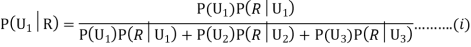
Since the three urns are equally likely to be selected
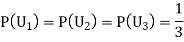
Also,
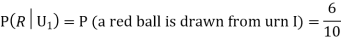
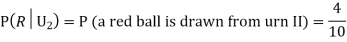

From (i), we have
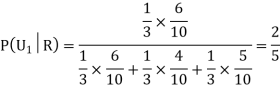
Question-8: An urn  contains 3 white and 4 red balls and an urn lI contains 5 white and 6 red balls. One ball is drawn at random from one of the urns and is found to be white. Find the probability that it was drawn from urn 1.
contains 3 white and 4 red balls and an urn lI contains 5 white and 6 red balls. One ball is drawn at random from one of the urns and is found to be white. Find the probability that it was drawn from urn 1.
Solution: Let 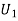 : the ball is drawn from urn I
: the ball is drawn from urn I
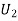 : the ball is drawn from urn II
: the ball is drawn from urn II
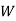 : the ball is white.
: the ball is white.
We have to find 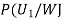
By Bayes Theorem
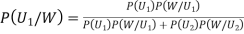 ... (1)
... (1)
Since two urns are equally likely to be selected,  (a white ball is drawn from urn
(a white ball is drawn from urn  )
) 
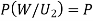 (a white ball is drawn from urn II)
(a white ball is drawn from urn II) 
From(1), 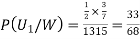
Question-9: ln a bolt factory machines 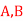 and
and  manufacturerespectively 25%, 35% and 40% of the total. lf their output 5, 4, and 2 percent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B.
manufacturerespectively 25%, 35% and 40% of the total. lf their output 5, 4, and 2 percent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B. ?
?
Solution: bolt is manufactured by machine 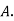
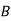 : bolt is manufactured by machine
: bolt is manufactured by machine 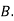
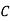 : bolt is manufactured by machine
: bolt is manufactured by machine 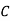
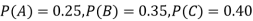
The probability of drawing a defective bolt manufactured by machine 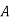 is
is 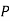 (D/A)
(D/A) 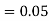
Similarly, 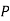 (D/B)
(D/B) 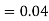 and
and  (D/C)
(D/C) 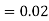
By Baye’s theorem
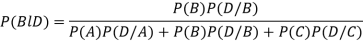
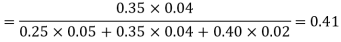
Question-10: Two discrete random variables X and Y have-
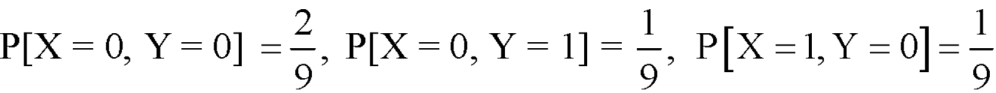
And
P[X = 1, Y = 1] = 5/9.
Check whether X and Y are independent or not?
Solution.
First, we write the given distribution In tabular form-
X/Y | 0 | 1 | P(x) |
0 | 2/9 | 1/9 | 3/9 |
1 | 1/9 | 5/9 | 6/9 |
P(y) | 3/9 | 6/9 | 1 |
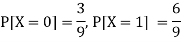
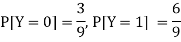
Now-
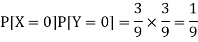
But
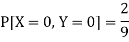
So that-
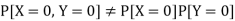
Hence X and Y are not independent.
Question-11: In a lottery, m tickets are drawn at a time out of tickets numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.
Solution. Let  be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
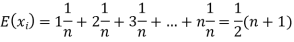
Therefore the expected value of the sum of the numbers on the tickets drawn
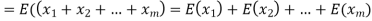

Question-12: X is a continuous random variable with probability density function given by
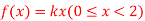
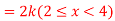
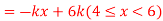
Find k and mean value of X.
Solution. Since the total probability is unity.
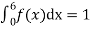
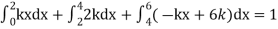
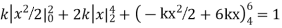
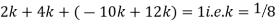
Mean of X =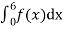
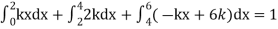
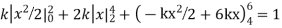
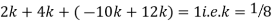
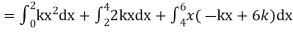
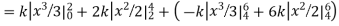
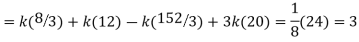
Question-13: If a random variable X has the following probability distribution in the tabular form then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | 1/4 | 1/2 | 1/4 |
Sol.
We know that-

So that-
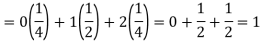
Question-14: I roll a fair die and let X be the resulting number. Find E(X), Var(X), and 
Solution. We have 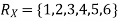 and
and 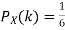 for k = 1,2,…,6. Thus we have
for k = 1,2,…,6. Thus we have

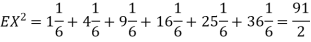
Thus,
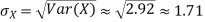
Question-15: The overall percentage of failures in a certain examination is 20. if 6 candidates appear in the examination what is the probability that at least five pass the examination?
Solution. Probability of failures = 20% 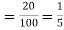
Probability of (P) = 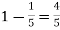
Probability of at least 5 passes = P(5 or 6)
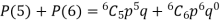
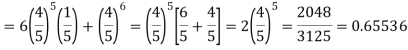
Question-16: Assuming that 20% of the population of a city are literate so that the chance of an individual being literate is  and assuming that a hundred investigators each take 10 individuals to see whether they are illiterate, how many investigators would you expect to report 3 or less were literate.
and assuming that a hundred investigators each take 10 individuals to see whether they are illiterate, how many investigators would you expect to report 3 or less were literate.
Solution. 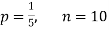
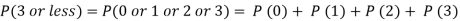
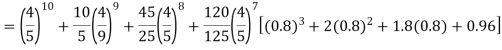
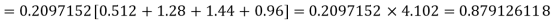
Required number of investigators = 0.879126118× 100 =87.9126118
= 88 approximate
Question-17: Assume that the probability of an individual coal miner being killed in a mine accident during a year is 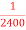 . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 miners, there will be at least one fatal accident in a year.
Solution. 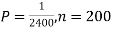


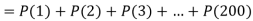
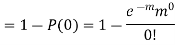
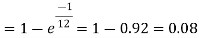
Question-18: The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise, the washers are considered defective. Determine the percentage of defective washers produced by the machine assuming the diameters are normally distributed.
Solution. 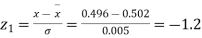
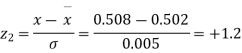
Area for non – defective washers = Area between z = -1.2
And z = +1.2
=2 Area between z = 0 and z = 1.2
=2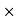 (0.3849)-0.7698=76.98%
(0.3849)-0.7698=76.98%
Percentage of defective washers = 100-76.98=23.02%
Question-19: The life of electric bulbs is normally distributed with mean 8 months and standard deviation 2 months.
If 5000 electric bulbs are issued how many bulbs should be expected to need replacement after 12 months?
[Given that P (z ≥ 2) = 0. 0228]
Solution.
Here mean (μ) = 8 and standard deviation = 2
Number of bulbs = 5000
Total months (X) = 12
We know that-
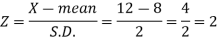
Area (z ≥ 2) = 0.0228
Number of electric bulbs whose life is more than 12 months ( Z> 12)
= 5000 × 0.0228 = 114
Therefore replacement after 12 months = 5000 – 114 = 4886 electric bulbs.
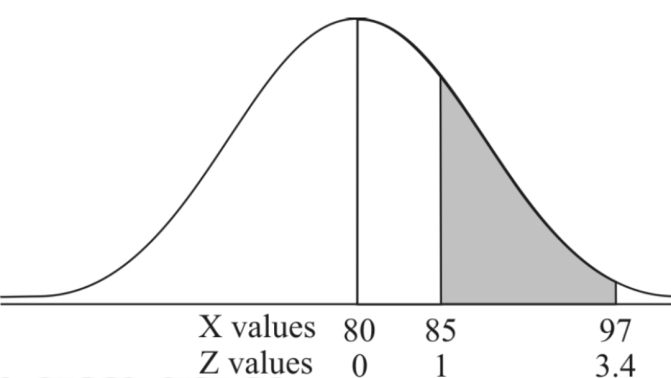
Question-20: If a random variable X is normally distributed with mean 80 and standard deviation 5, then find-
1. P[X > 95]
2. P[X < 72]
3. P [85 < X <97]
[Note- use the table- area under the normal curve]
Sol.
The standard normal variate is –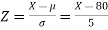
Now-
1. X = 95,
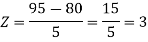
So that-
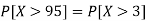
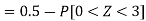
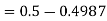


2. X = 72,

So that-
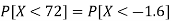
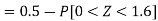

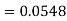
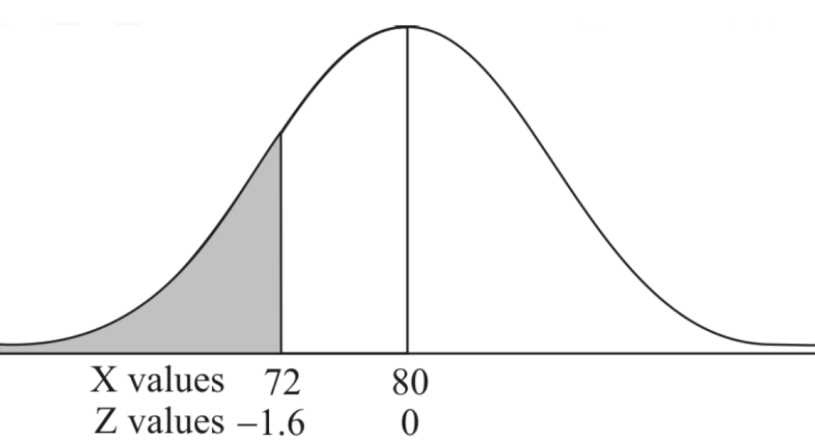
3. X = 85,

X = 97,
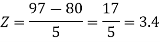
So that-