Unit - 2
Curves
Q1) What are the horizontal and vertical curve?
A1)
Horizontal curve:
- Definition: The curves which are provided at turning points so as to get gradual change in the direction of alignment of a road or a track are termed as horizontal curves.
- Note that these curves are in the horizontal plan. In railway track, the minimum radius of a horizontal curve should be 175 m for broad gauge.
- Horizontal as well as vertical, curves in case of road must ensure safety, comfort and convenience of the traffic.
Vertical Curve:
- Definition: The curves which are provided in the alignment of road or track at change of gradient is termed as vertical curves.
- Necessity of vertical curves: It gives adequate visibility and safety to the traffic.
- It gives gradual change in grade or slope.
- It gives adequate comfort to the passengers.
Q2) What are the different types of curves and their applications?
A2)
There are four types of horizontal curves:
- Simple curve
- Compound curve
- Reverse curve
- Transition curve
Simple curve:
- The curve which consists of a single arc of a circle of which two straight tangents further connects and brings about a deflection of the road through an angle '0' is called as simple curve. See Fig. For better understanding.
- Simple curve is normally represented by the length of its radius or by the degree of curve.
- This type of curve is provided at every change in alignment of the road or railway à track in a plain and in hilly areas.
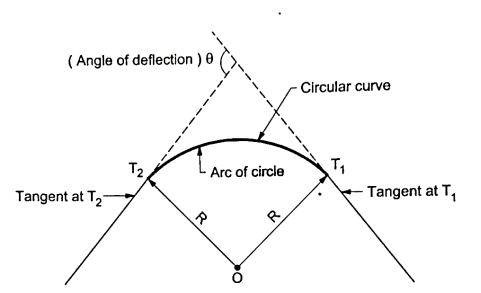
Fig.: Simple curve
Compound curves:
- A curve of having the series of two and more simple curves of different radii curving in the same direction is called as compound curves. Refer to the Fig.
For better understanding.
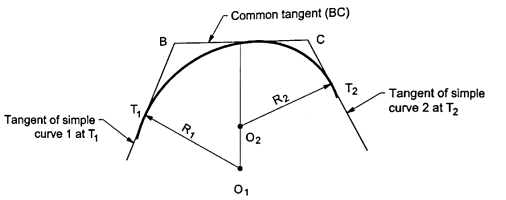
Fig.: Compound curve
- In compound curves, the two adjacent curves will have a common tangent "BC" as shown in Fig.
- The centers of two adjacent curve lie on the same side of the curve as shown in Fig.
- To avoid the cutting through hard rocks, heavy cutting or filling in the alignment of road or track, compound curves are provided.
Reverse curve:
- The curve which consists of two simple curves having equal or different radii turning in opposite direction is called as reverse curve. Refer to Fig. For better understanding.
- The two centres of curves are on opposite sides of a common tangent 'BD'.
- Reverse curves are necessary on hill roads where frequently changes in the direction of travel is required.
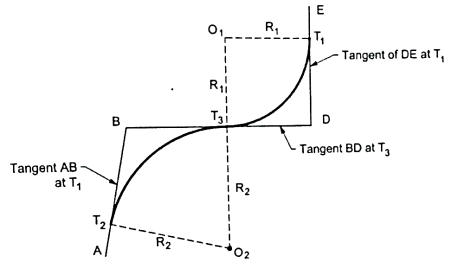
Fig.: Reverse curve
- Reverse curves are also necessary for cross-overs in station yards and in the alignment of the railway tracks in hilly areas.
Advantages of reverse curve:
- This type of curve is oftenly used in the alignment of a hill road.
- It is also used in the layout of railway spur tracks and cross-over.
Disadvantages of reverse curve:
- The use of reverse curve is not suitable on highways where the speeds are high.
- This type of curve is also not suitable in the main railway lines due to high speed.
- There is sudden change of direction in reverse curve and this makes passengers more uncomfortable.
- Steering is dangerous on highways and driver has to be very cautious.
Transition curve:
- The curve in which radius varies gradually from infinity to a finite value equal to that of the circular curve to be connected and vice versa is termed as transition curve.
- These curves are commonly used in railway tracks between the circular curve and a tangent so as to provide easy and gradual change in direction.
There are Two types of vertical curve:
- Summit Curve
- Valley Curve
Summit curves:
- Definition: The curves which are having convex surface on upward side is termed as summit curves.
- Vertical curves are used manly when rising gradient intersects a falling grade or when rising gradient meets another rising gradient or when rising gradient meets a horizontal road or when falling gradient meets at a steeper falling gradient. Refer Fig. For better understanding.
- Fig. Shows the different situations where summit curves are provided.
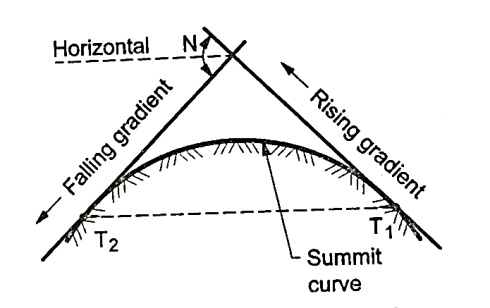
Fig.: A rising gradient intersecting a falling gradient
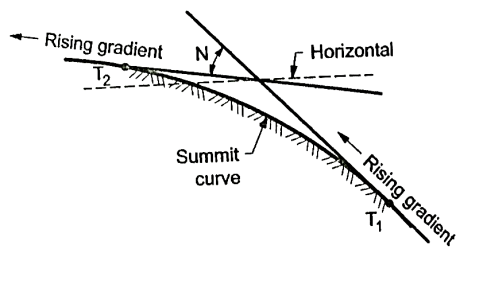
Fig.: A rising gradient meeting another rising gradient
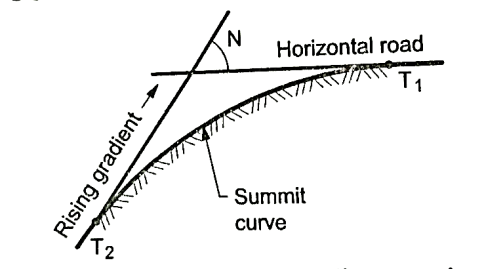
Fig.: A rising gradient meeting at horizontal road
Valley curves:
- Definition: The curves which are having the convex surface on downward side Fig. Shows the different situations where valley curves are termed as valley curve.
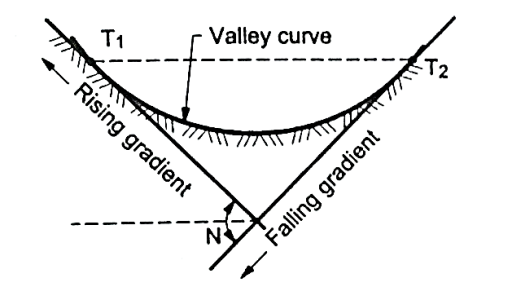
Fig.: A falling gradient intersecting a rising gradient
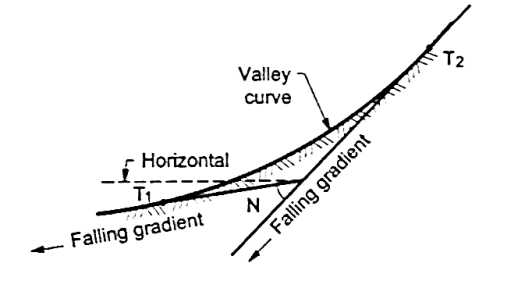
Fig.: A falling gradient meeting another falling gradient

Fig.: A falling gradient meeting a horizontal road
Q3) What are the elements of simple circular curve?
A3)
- Refer the Fig. For understanding the various terms of notation for a simple circular curve.
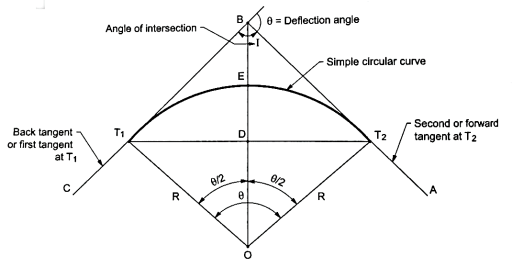
Fig.: Simple circular curve (Right hand curve)
- The common notation which are normally preferred for simple circular curve are as follows:
- BC and AB are the two tangents drawn to the curve at T1, and T2, respectively. In short, BC and AB are two straight called as tangents.
- The two tangents AB and BC are intersected at the B which is called as point of intersection. In short, B is the point of intersection of tangents AB and BC.
- In Fig., the curve deflects to right side. Therefore, it is called as right-hand curve.
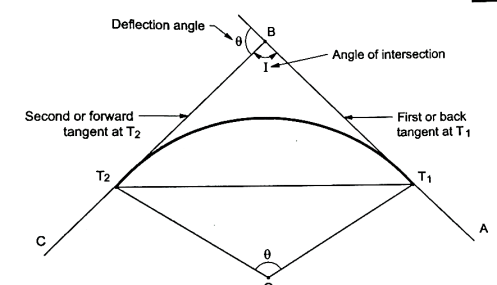
Fig.: Simple circular curve (left hand curve)
4. In Fig., the curve deflects to left side. Therefore, it is called as left-hand curve.
5. In Fig., BC is first tangent and also called as back tangent. AB is second tangent and also called as forward tangent. In Fig. AB is first or back tangent at T₁ and BC is second or forward tangent at T₁.
6. T1, and T2, are the tangent points. T1, shows the starting of the curve and T2, shows the end of the curve.
7. In fig., I is an angle of intersection and 0 is a deflection angle.
8. BT1, and B T2, are the lengths of tangent.
9. T1, T2, is a long chord of length 'L'.
10. The arc 'T1ET2' is a length of curve.
11. The mid-point 'E' is apex of summit of the curve T1ET2
12. BE is the distance of apex.
13. The angle 'T1OT2' = The deflection angle '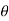 '.
'.
14. DE is a versed sine of the curves.
Q4) Explain the methods of setting out simple circular curve?
A4)
Radial offsets:
- Let Ox=Radial offset PN at any distance x along the tangent
T1P = x
From Δ T1 PO,
PO2 = T1O2+T1 P²
Ox=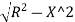 –R …... (1)
–R …... (1)
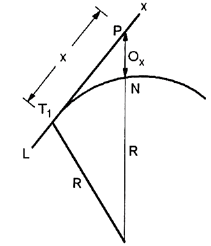
Fig.: setting out by radial offsets
- In order to get an approximate expression for Ox, expand

Thus,
Ox=R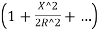 -R
-R
Neglecting the other terms except the first two, we get
Or Ox=x2/ 2R
When the radius is large
T1P2=PN(2R+PN)
X2=Ox(2R+Ox)
Neglecting Ox in comparison to 2R we get
Ox=x2/2R
Perpendicular offsets:
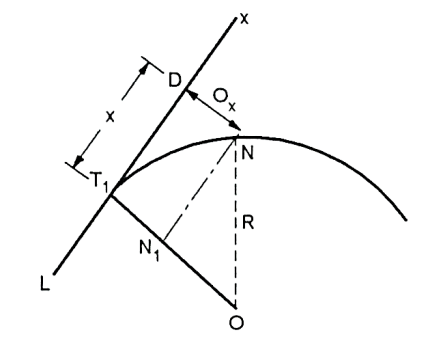
Fig.: setting out by perpendicular offsets
- Let DN=Ox= offset perpendicular to the tangent
T1D=x= measured along the tangent
Draw NN1 parallel to the tangent
From  leEE1O, we have
leEE1O, we have
E1O2=EO2-E1E2
(R-Ox)2=R2-x2
From which
Ox=R-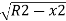
The corresponding approximate expression for Ox may be obtained by expanding the term . Thus,
. Thus,
Ox=R-R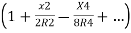
Neglecting the other terms except the first two of the expressions
Ox=R-R+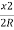
Q5) What is Transition curve?
A5)
- The curve in which radius varies gradually from infinity to a finite value equal to that of the circular curve to be connected and vice versa is termed as transition curve.
- These curves are commonly used in railway tracks between the circular curve and tangent so as to provide easy and gradual change in direction.
Necessity:
- To provide gradual change in the radius of curvature.
- To provide smooth entry of vehicle from a straight portion to curved portion.
- To permit gradual application of the superelevation and extra widening at horizontal curves.
- To provide safety to the vehicular traffic.
Q6) What is Super elevation?
A6)
It is defined as the raising of outer end of a road or outer rail over inner one.
h = super elevation = e
w = weight of vehicle
P = centrifugal force
g = acceleration due to gravity
R = radius of curve
G = gauge distance between rails
u = speed of vehicle
B = width of pavement
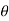 = Angle of super elevation
= Angle of super elevation
h = super elevation = e
w = weight of vehicle
P = centrifugal force
g = acceleration due to gravity
R = radius of curve
G = gauge distance between rails
u = speed of vehicle
B = width of pavement
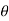 = Angle of super elevation
= Angle of super elevation
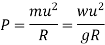
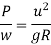

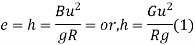
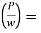 Centrifugal ratio
Centrifugal ratio
Q7) What are the characteristics of Transition curve?
A7)
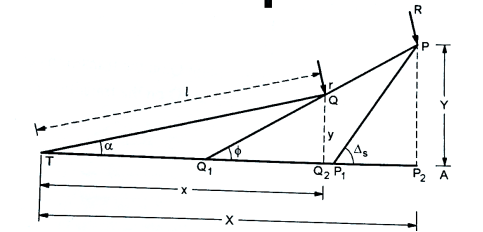
Fig.: Transition curve
Let TB = the original tangent
T= the starting of the transition curve
P= the end of the transition curve
PP₂= the tangent to both the transition and circular curve at P
Y = PP1=the offset to junction point (P) of both curves.
X = TP1=the x coordinate of P
PP’= the redundant circular curve
T₁ = the point of intersection of the line OP’ perpendicular to the tangent to the circular curve at P and original tangent AB.
S=ET1= the shift of the circular curve
N =the point in which OP’ cuts the transition curve
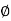 ₁ = the spiral angle between the common tangent PP2and the original TB
₁ = the spiral angle between the common tangent PP2and the original TB
R = the radius of the circular curve (OP)
L = the length of the transition curve
1) Now PP’=R
But 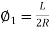
∴PP’=R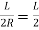
Since PN is very nearly equal to PP’
∴EN =
i.e., the shift (PT1) bisects the transition curve at N
Hence TN =1/2
2) Draw PG perpendicular to OP’
Now, S = P’T₁=GT₁-GP’
= PP’-GE’
S = Y-R (1-cos 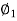 )
)
Or S=Y-2Rsin2
But Y=
S=Y-2Rsin2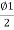
=Y-2R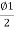
2R sin² S=Y-2R sin
=Y-2R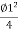
=
S=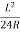
Also, NT1 = 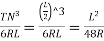
NT₁ =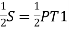
i.e., the transition curve bisects the shift.
(3) Total tangent length (BT):
(a) True Spiral
BT = BT1+T1T
Now T1T=TP1-P1T1
=TP1-PG
=X-Rsin
OT1= OP' + P'T1
= R+S
BT1=(R+S) tan
Where  is the deflection angle between the straights.
is the deflection angle between the straights.
∴BT = (R+S) tan + (X-R sin
+ (X-R sin )
)
Now,
X=L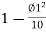 and
and 
∴BT=(R+S) tan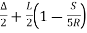
Q8) What is the equation of Clothoid?
A8)
The centrifugal force acting on a vehicle is given by
P=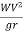
Fig
Where,
r-is the radius of curvature at any point on the curve
If the centrifugal force P is to increase at a constant rate, P must vary with time
Also, if the speed of the vehicle is constant, the distance I along the transition curve measured from the tangent point must vary with time.
Hence, we have
P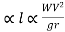
But W1V and g are all constants
Hence l …… (1)
…… (1)
Lr=constant=LR
Thus, the fundamental requirement of a transition curve is that its radius of the curvature at any point shall vary inversely as the distance (l) from the beginning of the curve. Such a curve is the clothoid curve is also known as the ideal transition curve.
Let
T= tangent point = beginning of the transition curve
TA= initial tangent
P= point of junction of the transition circular curve
Q = any point on the curve at distance I along the curve.
r = radius of the curve at any point Q
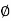 = the inclination of the tangent to the transition curve at Q to the initial
= the inclination of the tangent to the transition curve at Q to the initial
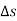 = spiral angle = the angle between the initial tangent and the tangent to the transition curve at the junction point E
= spiral angle = the angle between the initial tangent and the tangent to the transition curve at the junction point E
l= length of the curve from T to B
R= radius of the circular curve
X = the x coordinate of P
Y = the y coordinate of P
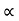 = TQ₂ = x coordinate of any point Q on the transitions curve
= TQ₂ = x coordinate of any point Q on the transitions curve
Y = OQ2= y coordinate to any point Q on the transition curve.
We have,
Lr = LR=Constant
Or 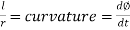
Integrating both side
We get
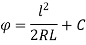
When l=0,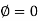
∴C=0
Hence 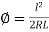
This is the intrinsic equation of the ideal transition curve.
Equation can also be expressed as
l =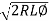
1 = K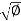
Where
k = 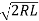
When L=l,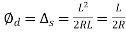
Q9) What is the equation of Cubic Parabola curve?
A9)
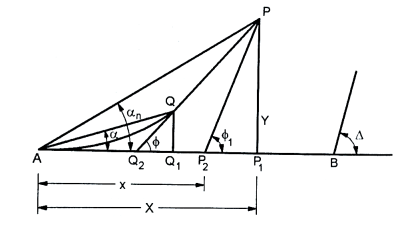
Fig.: Cubic parabola curve
Let x = AQ₁ = The distance of any point Q on the tangent AB from the commencement A of the curve.
y = Q, Q=the perpendicular offset to the point Q
I= the length of the transition curve AQ
X = AP, the distance of the junction point P on transition curve with the circular curve from A measured along AB.
Y = PP the Perpendicular offset to the junction point P
L= the length of the transition curve.
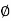 = QQ2B= the angle between the tangent line AB and the tangent to the transition curve at any point Q
= QQ2B= the angle between the tangent line AB and the tangent to the transition curve at any point Q
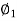 = PP2B= the angle between AB and the tangent at P (Spiral angle)
= PP2B= the angle between AB and the tangent at P (Spiral angle)
R= the radius of the circular curve
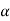 = ∠QAB = the deflection angle to any point Q
= ∠QAB = the deflection angle to any point Q
a = ∠PAB = the deflection angle to the junction P
y =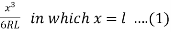
Now, tan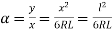
From the intrinsic equation,
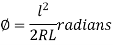
∴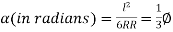
 …. (2)
…. (2)
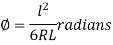
=
=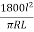 minutes …. (3)
minutes …. (3)
Since l=L,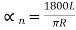 … (4)
… (4)
=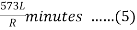
If the degree (D) of the curve be given instead of radius, the corresponding values of
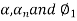 may be found by substituting the value of R in terms of D, viz
may be found by substituting the value of R in terms of D, viz 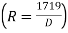 in equation 3 & 5.
in equation 3 & 5.
Hence,  …. (6)
…. (6)
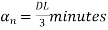 …. (7)
…. (7)
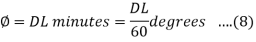
From equation (1), the Co-ordinates of P are
X = L and Y=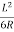 = four times the shift
= four times the shift
Total tangent length = BA= (R+ Stan)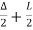
In which
S= the shift and
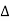 = the deflection angle between the two tangent S.
= the deflection angle between the two tangent S.
Q10) Two straights intersect at a chainage of 2610 m, the deflection angle being 36 A circular curve of 400 m radius is to be set. Calculate the chainages of the tangent point of right-handed circular curve. Peg interval is 30 m.
A10)
Given: Deflection angle (0) = 36°.
BT₁ Tangent length = R tan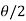 =400
=400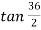 129.967 =129.97 m
129.967 =129.97 m
= (4+9.97) chains
Length of curve = =
=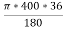 =251.327=251.33m
=251.327=251.33m
= (8+11.33) chains
Chainage of the second tangent point "T1':
=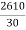 -(4+9.97) chains
-(4+9.97) chains
= (87) -(4+9.97) chains
= (83+9.97) chains
Chainage of the second tangent point ‘T2':
= (Chainage of T,) + (length of curve)
= (83 +9.97) + (8 +11.33)
= (91 +21.3) chains
Q11) Two roads meet at an angle of 150. Calculate the data necessary for setting out curve of 10 chains radius to connect the two straight roads if it intended to set out curve by chain and offset from long chord, chain used is a 30 m chain only. Calculate two offsets from centre of long chord.
A11)
Given:
I =point of intersection
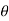 =deflection angle = 180° - 150° = 30°
=deflection angle = 180° - 150° = 30°
R = radius of curve = 10 chains = 10x30=300 m (since 30 m chain used)
Length of long chord (L) =2 R sin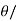 2
2
L = 2x300 x sin 30°/2 = 155.29 m
Note: Length of long chord is taken in round figures as 160 m.
∴L = 160 m
Ordinate at the middle of the long chord (O)= versed sine
O0 = R-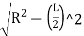
=300-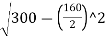
O0=300-289.136
∴O0=10.86 m
The various ordinates can be calculated by the following formula as,
Ox=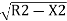 –(R-O0)
–(R-O0)
Consider the offset at 20 m from the centre.
O20=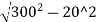 -(300-10.86)
-(300-10.86)
=299.33-289.14=10.19 m
(It is the first offset from the centre of long chord)
O40=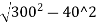 -(300-10.86)
-(300-10.86)
=297.32-289.14=8.18m
(It is the second offset from the centre of long chord.)
Hence the two offsets from the center of long chord are 10.19 m and 8.18 m.
Extension of problem:
Remaining offsets till curve ends can be calculated as follows:
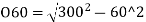 -(300-10.86)
-(300-10.86)
=293.938-289.14
=4.8 m
O80=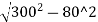 -(300-10.86)
-(300-10.86)
=289.136-289.14
=0 m