Unit 2
Energy-Depth relationship
Q1: A rectangular channel with a bottom width of 4 m and a bottom slope of 0.0008 has a discharge of 150m3/s. In gradually varied flow in this channel, the depth at certain location is found to be 0.30 m. Assuming n = 0.016, determine the type of GVF profile.
Solution: a)
Q =  A R2/3 S1/2
A R2/3 S1/2
1.5 = 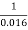 X B Yo X
X B Yo X 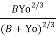 X
X 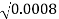
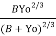 = 0.8485238157
= 0.8485238157
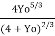 = 0.848528157
= 0.848528157
By trial and error method, we get
Yo = 0.426 m
a) Critical Depth
q = Q/B = 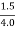 = 0.375 m3/s/m
= 0.375 m3/s/m
Yc = (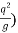 1/3 = (
1/3 = (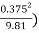 1/3
1/3
= 0.243 m
b) Type of profile
Since Yo > Yc; the channel is a mid slope channel. Also, given y -= 0.30 m is such that
Yo > Y > Yc
As such profile is of the M2 type.
Q2: Water flowing in triangular channel of side slope 1 horizontal and 1 vertical and longitudinal slope of 0.002. Determine whether the channel is mild, steep or critical when a discharge of 0.2m3/s flow through it. Assume Manning’s n = 0.0015. For what range of depth will the flow be type of 1, 2 or 3?
Solution:
For a depth of flow of y in the channel
A = Y2
T = 2Y
R = 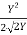 =
= 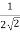 Y
Y
Critical depth Yc:
 =
= 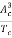 =
= 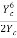 =
= 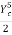
Yc = (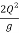 ) 1/5 = (
) 1/5 = (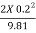 ) 1/5
) 1/5
= 0.382 m
Normal Depth Yo:
Q =  A Ro 2/3 So ½
A Ro 2/3 So ½
=  (Yo) 2 X
(Yo) 2 X 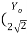 )2/3 S01/2
)2/3 S01/2
=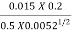 = 0.13416
= 0.13416
Yo = 0.471 m
Since Yo > Yc, the channel is a mild slope channel for this discharge. If Y is the depth of flow
For M1 curve Y > 0.471 m
For M2 curve 0.471 > Y > 0.382 m
For M3 curve Y < 0.382 m
Q3: A wide rectangular channel has a Manning’s coefficient of 0.018. For a discharge intensity of 1.5m3/s/m. Identify the possible type of gradually varied profile produced in the following break in the grade of the channel.
a) So1 = 0.003 and So2 = 0.016
b) So1 = 0.015 and So2 = 0.0003
Solution:
Discharge intensity q = 1.5m3/s/m
Critical depth Yc = ( 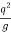 ) 1/3 = (
) 1/3 = ( 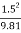 ) 1/3
) 1/3
= 0.613 m
Normal depth Yo = for wide rectangular channel
R = Yo
q =  Yo X Yo2/3 X So1/2
Yo X Yo2/3 X So1/2
Yo = (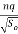 ) 3/5 = (
) 3/5 = (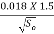 ) 3/5
) 3/5
Value of Slope Value of Yo
0.003 1.305 m
0.015 0.404 m
0.016 0.396 m
Case Yc Yo1 Yo2 Type of grade change
a) 0.612 1.305 0.396 Mild to Steep
b) 0.612 0.404 1.305 Steep to Mild
Case a): Possible types of profile are M2 and S2.
Case b):
- M3 curve and a jump or
- Jump and S1 curve
- In a limiting case of (i) and (ii) the jump may occur of the break in grade and here will be no GVF profile in a case.
Q4: Show that differential equation gradually varied flow in a rectangular channel of variable width B can be expressed as
 =
= 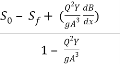
Solution: We know gradually varied flow equation
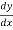 =
= 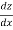 +
+  +
+ 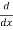 (
(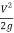 ) -------------------------1
) -------------------------1
But we know that, 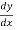 = -Sf,
= -Sf,  = -So
= -So
Putting these value in equation 1
-Sf = -So + 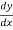 +
+ 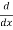 (
(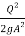 )
)
So – Sf =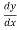 +
+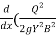 )
)
So – Sf = 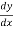 +
+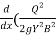 ) X
) X 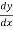 +
+ 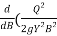 )
)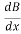
So – Sf = 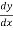 -
- 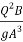
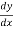 -
- 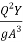
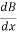
On rearranging, we get
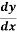 =
= 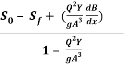
Q5: Show that for horizontal, frictionless rectangular channel of varying width B, the above relation reduces to
(1 – F2)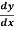 -F2 (
-F2 ( )
) 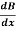 = 0 Where, F = Froude Number
= 0 Where, F = Froude Number
Solution: From above equation proved in previous question,
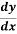 =
= 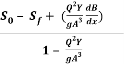
As, in case if horizontal, frictionless rectangular channel,
So = 0 and Sf = 0, we get
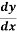 =
= 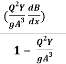 -------------------------1
-------------------------1
We know that,
Froude number, F = 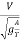
Or, F2 = 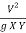 (In case of rectangular channel
(In case of rectangular channel  = Y)
= Y)
Or, F2 = 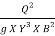 (Where q = Q/B)
(Where q = Q/B)
Or, F2 = 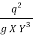
Or, F2 = 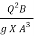 ---------------------------2
---------------------------2
Putting this value in equation (1), we get
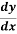 =
= 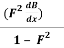
Hence, (1 – F2)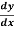 -F2 (
-F2 ( )
) 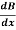 = 0 Where, F = Froude Number
= 0 Where, F = Froude Number
Q6: Show that for a wide rectangular channel the slope is mild or steep according to So being less or greater than
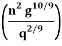
Solution: a).To finds normal depth
Q =  A Ro 2/3 So ½ --------------------------1
A Ro 2/3 So ½ --------------------------1
For wide rectangular channel R = Y0
Q = 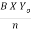 X Yo2/3 X So1/2
X Yo2/3 X So1/2
q = 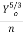 So1/2
So1/2
Yo = (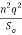 ) 5/3 ----------------------------2
) 5/3 ----------------------------2
b) To find critical depth
Yc = (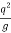 ) 1/3
) 1/3
For mild slope
(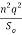 ) 3/10 > (
) 3/10 > (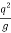 ) 1/3
) 1/3
So < (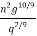 )
)
Similarly for steep slope channel
Yo < Yc
(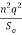 ) 3/10 < (
) 3/10 < (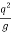 ) 1/3
) 1/3
So > (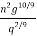 )
)
Q7: For a wide rectangular channel, if the Manning’s formula is used, the differential equation of GVF become
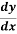 = So
= So 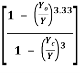
Solution: The form is basic differential is given by
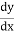 =
= 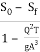
= So 
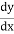 = So
= So  ------------------------1
------------------------1
Where, K = Conveyance of one channel
K =  A R2/3
A R2/3
K =  B Y5/3
B Y5/3
Similarly for Ko
Ko =  B Yo 5/3, Hence
B Yo 5/3, Hence 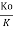 =
=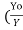 )5/3 ------------------2
)5/3 ------------------2
Now, we know that
Z2 = C1YM
Where, M = First hydraulic exponent
For rectangular channel, M = 3
Hence, Z2 = C1Y3
Zc 2 = C1Yc M
 ) 2 =
) 2 = ) 3 ---------------------------3
) 3 ---------------------------3
Putting this value is equation (1) we get
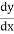 = So
= So 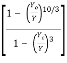
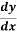 = So
= So 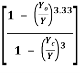
Q8: For a very wide rectangular channel, if Chezy’s formula is used, the differential equation of GVF is given by
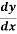 = So
= So 
Solution: The basic GVF equation is given by
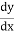 =
= 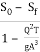
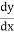 = So
= So  ---------------1
---------------1
By assumption (2) of GVF
Q = CA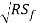 ---- 2 (For wide rectangular channel R = y)
---- 2 (For wide rectangular channel R = y)
Q = C X By  --------------------------3
--------------------------3
For normal discharge Q = C X B Yo X 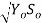 --------------------------4
--------------------------4
Dividing equations (3) and (4), we get
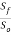 = (
= (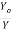 ) 3-----------------------5
) 3-----------------------5
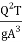 = (
= (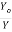 ) 3 ----------------------6
) 3 ----------------------6
Putting this value in equation (1), we get
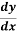 = So
= So 
Q9: A wide rectangular channel of slope 0.0003 and n = 0.02 connects two reservoir 1.5k m apart. The upstream reservoir level is constant at an elevation of 104.00 m and the elevation of canal is constant at the intake is 101.00 m. The intake is free and the loss of energy at the intake can be neglected. a) What should be the downstream level to cause uniform flow in the entire length of the channel?
Solution:
Neglecting losses at the entry
H = Yo + 
As the channel is wide,
Vo =  Yo2/3 So1/2
Yo2/3 So1/2
Yo = H - 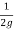 (
( Yo2/3 So1/2)2
Yo2/3 So1/2)2
Yo = 30 - 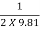 (
(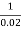 Yo2/3 0.0003)
Yo2/3 0.0003)
Solving by trial and error method,
Yo = 2.70 m
Bed unit downstream end of the channel i.e., at the section B.
= 101 – (0.003 X 1500)
= 100.55 m
Downstream pool elevation,
= 100.55 + 2.70
= 103.25 m
Q10: In a rectangular channel 12 m wide and 3.6 m deep water is flowing with a velocity of 1.2 m/s. The bed slope of the channel is 1/4000. If the flow of water is through the channel is regulated in such a way that energy line depth of water having a slope of 0.00004. Find the rate of change of depth of water in the channel?
Solution:
Width of channel, b = 12 m
Depth of channel, y = 3.6 m
Velocity of flow, v = 1.2 m/s
Bed slope, Sf = 1/4000 =0.00025
Slope of energy line, Se = 0.00004
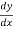 = ?
= ?
 =
= 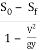
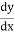 =
= 
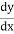 = 0.0002189
= 0.0002189
Unit 2
Energy-Depth relationship
Q1: A rectangular channel with a bottom width of 4 m and a bottom slope of 0.0008 has a discharge of 150m3/s. In gradually varied flow in this channel, the depth at certain location is found to be 0.30 m. Assuming n = 0.016, determine the type of GVF profile.
Solution: a)
Q =  A R2/3 S1/2
A R2/3 S1/2
1.5 = 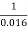 X B Yo X
X B Yo X 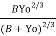 X
X 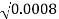
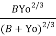 = 0.8485238157
= 0.8485238157
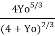 = 0.848528157
= 0.848528157
By trial and error method, we get
Yo = 0.426 m
a) Critical Depth
q = Q/B = 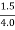 = 0.375 m3/s/m
= 0.375 m3/s/m
Yc = (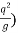 1/3 = (
1/3 = (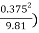 1/3
1/3
= 0.243 m
b) Type of profile
Since Yo > Yc; the channel is a mid slope channel. Also, given y -= 0.30 m is such that
Yo > Y > Yc
As such profile is of the M2 type.
Q2: Water flowing in triangular channel of side slope 1 horizontal and 1 vertical and longitudinal slope of 0.002. Determine whether the channel is mild, steep or critical when a discharge of 0.2m3/s flow through it. Assume Manning’s n = 0.0015. For what range of depth will the flow be type of 1, 2 or 3?
Solution:
For a depth of flow of y in the channel
A = Y2
T = 2Y
R = 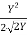 =
= 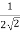 Y
Y
Critical depth Yc:
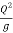 =
= 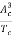 =
= 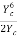 =
= 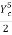
Yc = (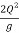 ) 1/5 = (
) 1/5 = (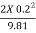 ) 1/5
) 1/5
= 0.382 m
Normal Depth Yo:
Q =  A Ro 2/3 So ½
A Ro 2/3 So ½
=  (Yo) 2 X
(Yo) 2 X 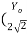 )2/3 S01/2
)2/3 S01/2
=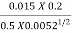 = 0.13416
= 0.13416
Yo = 0.471 m
Since Yo > Yc, the channel is a mild slope channel for this discharge. If Y is the depth of flow
For M1 curve Y > 0.471 m
For M2 curve 0.471 > Y > 0.382 m
For M3 curve Y < 0.382 m
Q3: A wide rectangular channel has a Manning’s coefficient of 0.018. For a discharge intensity of 1.5m3/s/m. Identify the possible type of gradually varied profile produced in the following break in the grade of the channel.
a) So1 = 0.003 and So2 = 0.016
b) So1 = 0.015 and So2 = 0.0003
Solution:
Discharge intensity q = 1.5m3/s/m
Critical depth Yc = ( 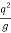 ) 1/3 = (
) 1/3 = (  ) 1/3
) 1/3
= 0.613 m
Normal depth Yo = for wide rectangular channel
R = Yo
q =  Yo X Yo2/3 X So1/2
Yo X Yo2/3 X So1/2
Yo = ( ) 3/5 = (
) 3/5 = (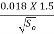 ) 3/5
) 3/5
Value of Slope Value of Yo
0.003 1.305 m
0.015 0.404 m
0.016 0.396 m
Case Yc Yo1 Yo2 Type of grade change
a) 0.612 1.305 0.396 Mild to Steep
b) 0.612 0.404 1.305 Steep to Mild
Case a): Possible types of profile are M2 and S2.
Case b):
- M3 curve and a jump or
- Jump and S1 curve
- In a limiting case of (i) and (ii) the jump may occur of the break in grade and here will be no GVF profile in a case.
Q4: Show that differential equation gradually varied flow in a rectangular channel of variable width B can be expressed as
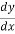 =
= 
Solution: We know gradually varied flow equation
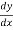 =
= 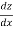 +
+  +
+ 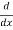 (
(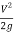 ) -------------------------1
) -------------------------1
But we know that, 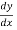 = -Sf,
= -Sf, 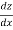 = -So
= -So
Putting these value in equation 1
-Sf = -So + 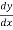 +
+ 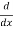 (
(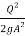 )
)
So – Sf =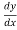 +
+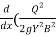 )
)
So – Sf = 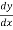 +
+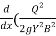 ) X
) X  +
+ 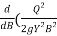 )
)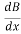
So – Sf =  -
- 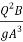
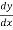 -
- 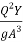
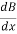
On rearranging, we get
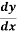 =
= 
Q5: Show that for horizontal, frictionless rectangular channel of varying width B, the above relation reduces to
(1 – F2) -F2 (
-F2 ( )
)  = 0 Where, F = Froude Number
= 0 Where, F = Froude Number
Solution: From above equation proved in previous question,
 =
= 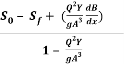
As, in case if horizontal, frictionless rectangular channel,
So = 0 and Sf = 0, we get
 =
= 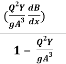 -------------------------1
-------------------------1
We know that,
Froude number, F = 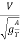
Or, F2 =  (In case of rectangular channel
(In case of rectangular channel  = Y)
= Y)
Or, F2 = 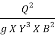 (Where q = Q/B)
(Where q = Q/B)
Or, F2 = 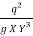
Or, F2 = 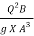 ---------------------------2
---------------------------2
Putting this value in equation (1), we get
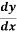 =
= 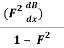
Hence, (1 – F2) -F2 (
-F2 ( )
) 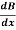 = 0 Where, F = Froude Number
= 0 Where, F = Froude Number
Q6: Show that for a wide rectangular channel the slope is mild or steep according to So being less or greater than
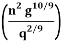
Solution: a).To finds normal depth
Q =  A Ro 2/3 So ½ --------------------------1
A Ro 2/3 So ½ --------------------------1
For wide rectangular channel R = Y0
Q = 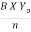 X Yo2/3 X So1/2
X Yo2/3 X So1/2
q =  So1/2
So1/2
Yo = ( ) 5/3 ----------------------------2
) 5/3 ----------------------------2
b) To find critical depth
Yc = (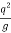 ) 1/3
) 1/3
For mild slope
(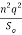 ) 3/10 > (
) 3/10 > (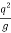 ) 1/3
) 1/3
So < (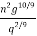 )
)
Similarly for steep slope channel
Yo < Yc
( ) 3/10 < (
) 3/10 < (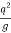 ) 1/3
) 1/3
So > (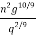 )
)
Q7: For a wide rectangular channel, if the Manning’s formula is used, the differential equation of GVF become
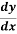 = So
= So 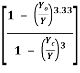
Solution: The form is basic differential is given by
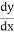 =
= 
= So 
 = So
= So  ------------------------1
------------------------1
Where, K = Conveyance of one channel
K =  A R2/3
A R2/3
K =  B Y5/3
B Y5/3
Similarly for Ko
Ko =  B Yo 5/3, Hence
B Yo 5/3, Hence 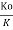 =
=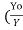 )5/3 ------------------2
)5/3 ------------------2
Now, we know that
Z2 = C1YM
Where, M = First hydraulic exponent
For rectangular channel, M = 3
Hence, Z2 = C1Y3
Zc 2 = C1Yc M
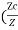 ) 2 =
) 2 =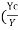 ) 3 ---------------------------3
) 3 ---------------------------3
Putting this value is equation (1) we get
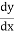 = So
= So 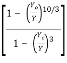
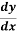 = So
= So 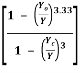
Q8: For a very wide rectangular channel, if Chezy’s formula is used, the differential equation of GVF is given by
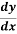 = So
= So 
Solution: The basic GVF equation is given by
 =
= 
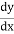 = So
= So  ---------------1
---------------1
By assumption (2) of GVF
Q = CA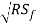 ---- 2 (For wide rectangular channel R = y)
---- 2 (For wide rectangular channel R = y)
Q = C X By  --------------------------3
--------------------------3
For normal discharge Q = C X B Yo X 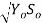 --------------------------4
--------------------------4
Dividing equations (3) and (4), we get
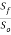 = (
= (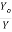 ) 3-----------------------5
) 3-----------------------5
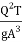 = (
= (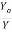 ) 3 ----------------------6
) 3 ----------------------6
Putting this value in equation (1), we get
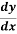 = So
= So 
Q9: A wide rectangular channel of slope 0.0003 and n = 0.02 connects two reservoir 1.5k m apart. The upstream reservoir level is constant at an elevation of 104.00 m and the elevation of canal is constant at the intake is 101.00 m. The intake is free and the loss of energy at the intake can be neglected. a) What should be the downstream level to cause uniform flow in the entire length of the channel?
Solution:
Neglecting losses at the entry
H = Yo + 
As the channel is wide,
Vo =  Yo2/3 So1/2
Yo2/3 So1/2
Yo = H -  (
( Yo2/3 So1/2)2
Yo2/3 So1/2)2
Yo = 30 - 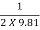 (
(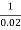 Yo2/3 0.0003)
Yo2/3 0.0003)
Solving by trial and error method,
Yo = 2.70 m
Bed unit downstream end of the channel i.e., at the section B.
= 101 – (0.003 X 1500)
= 100.55 m
Downstream pool elevation,
= 100.55 + 2.70
= 103.25 m
Q10: In a rectangular channel 12 m wide and 3.6 m deep water is flowing with a velocity of 1.2 m/s. The bed slope of the channel is 1/4000. If the flow of water is through the channel is regulated in such a way that energy line depth of water having a slope of 0.00004. Find the rate of change of depth of water in the channel?
Solution:
Width of channel, b = 12 m
Depth of channel, y = 3.6 m
Velocity of flow, v = 1.2 m/s
Bed slope, Sf = 1/4000 =0.00025
Slope of energy line, Se = 0.00004
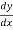 = ?
= ?
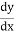 =
= 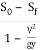
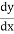 =
= 
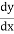 = 0.0002189
= 0.0002189