Unit 3
Rapidly varied flow
Q1: A stationary hydraulic jump occurs in a rectangular channel with the initial and sequent depth being equal to 0.30 m and 1.20 m respectively. Estimate (i) discharge per unit width (ii) Energy loss.
Solution:

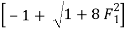
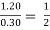
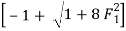
F1 = 3.162
F1 = 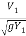 =
=  = 3.162
= 3.162
(i) Discharge per unit width q = V1Y1 = 5.424 X 0.30
=1.6272 m3/s/m
(ii) Energy Loss
EL = 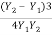 =
= 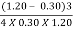
EL = 0.506 m
Q2: If in a hydraulic jump occurring in a horizontal rectangular channel, then the Froude number before the jump is 10.0 and the energy loss is 3.10 m. Estimate the sequents depth.
Solution:
The sequent depth ratio
For, F1 = 10
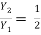
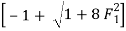
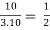
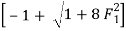
= 13.651
Energy loss
EL = 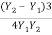
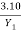 =
= 
Y1 = Depth before the jump = 0.0836 m
Y2 = Depth after the jump = 1.141 m. Since 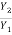 = 13.651
= 13.651
Q3: In a hydraulic jump occurring in a rectangular channel of 3.0 m width, the discharge is 7.8m3/s and the depth before the jump is 0.30 m. Estimate the (i) sequent depths and (ii) the energy loss in the jump.
Solution:
i) V1 = Q/A =  = 8.67 m/s
= 8.67 m/s
F1 = 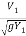 =
= 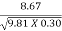 = 5.054
= 5.054
The sequent depth is given by
For F1 = 5.054, 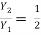
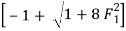
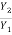 = 6.664
= 6.664
Y2 = 6.664 X 0.03 = 1.99 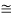 2 m
2 m
Y1 = 0.30 m
Ii) Energy loss
EL = 
= (2 -3)3 / 4 X 2 X 3
= 2.047 m
Q4: A rectangular channel carrying a supercritical stream is to be provided with a hydraulic jump type of energy dissipater. It is desired to have an energy loss of 4.0 m in the hydraulic jump when the inlet Froude number is 8.5. What are the sequent depths in the jump?
Solution:
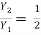
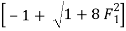
= 
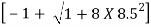
= 11.53
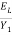 =
= 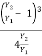
 =
= 
Y1 = 0.158 m
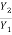 = 11.53
= 11.53
Y2 = 11.53 X 0.158
= 1.822 m
Q5: An overflow spillway is 40.0 m high. At the design energy head of 2.5 m over the spillway. Find the sequent depths. Neglect energy loss due to flow over the spillway face. (Assume Cd = 0.68)
Solution:
q =  Cd
Cd  X Hd3/2
X Hd3/2
=  X 6.8 X
X 6.8 X 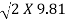 X (2.5)3/2
X (2.5)3/2
= 7.93m3/s/m
By using the equation
P + Hd = Y1 + 
(Energy loss over the spillway is neglected)
Y1 + 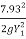 = 42.5
= 42.5
Y1 = 0.28 m
V1 = 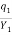 =
= 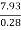 = 28.32 m/s
= 28.32 m/s
F1 = 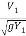 =
= 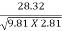
= 17.088
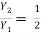
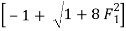
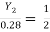
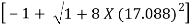
Y2 = 6.627 m
Q6: For a hydraulic jump in a rectangular channel the velocity and depth after the jump are known to be 0.80 m/s and 1.75 m. Calculate the depth before the jump and the energy loss and the power dissipated per meter width.
Solution:
F2 =  =
= 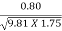 = 0.1931
= 0.1931
The sequent ratio is given in terms of F2 as
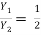
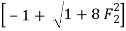
= 
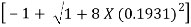
 = 0.0697
= 0.0697
Y1 = 0.0697 X 1.75 = 0.122 m
Energy loss,
EL = 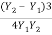
= 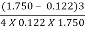
= 5.054 m
The power dissipated, P = 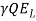
= 9790 X (0.80 – 1.75) X 5.054
= 69270 watt/m width
Q7: A hydraulic jump occurs in a rectangular channel and the depth of flow before and after the jumps are 0.5 and 0.20 m. Calculate the critical depth.
Solution:
Y1 = 0.5 m and Y2 = 0.20 m
The sequent depths are related to critical depth is as follow:
Y1 Y2 (Y1 + Y2) = 2 Yc3
Yc = 0.327 m
Q8: Show that the Froude number F1 and F2 before and after jump respectively, in a hydraulic jump taking place in a rectangular channel are related as:
F22 = 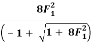
Solution:
F22 = 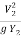 =
= 
= 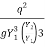 =
= 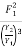
The sequent depth ratio 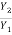 is related to F1 as
is related to F1 as
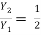

F22 = 
Q9: In a tidal river the depth and velocity of flow are 0.8 m and 1.25 m/s. Due to tidal action, a tidal bore of height 1.2 m is observed to travel upstream. Estimate the height and speed of the bore after the passage of the bore.
Solution: Let Vw (directed downstream) be the velocity of the bore. Superimpose a velocity (-vw) on the system to get stimulated as shown:
Here, Y1 = 0.8m and v1 = 1.25 m/s
Y2 = 0.8 + 1.2 =2.0 m
For positive surge moving in the upstream direction,
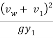 =
=  (
(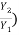 (
(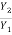 + 1)
+ 1)
(vw + 1.25 )2 = 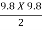 X
X 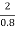 X (
X (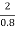 + 1)
+ 1)
Vw = 4.61 m/s
By continuity equation
Y2 (vw + v2) = Y1 (vw + v1)
2 (4.61 + v2) = 0.8 (4.61 + 1.25)
V2 = -2.26 m/s
The river has a velocity of 2.26 m/s directed upstream after the passage of the bore.
Q10: A sluice gate in a wide channel controls the flow of water. When the flow in the downstream channel at a depth of 3.0 m with a velocity of 4.0 m/s. The sluice gate was partially closed, instantaneously to reduce the discharge to 25% of its initial value. Estimate the velocity and depth at the gate.
Solution:
Let suffix 1 refers to the flow condition before the gate closure and suffix 2 conditions after the passage of the negative wave.
Prior velocity, V1 = 4.0 m/s
New discharge intensity, q = 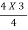 = 3.0 m/s = V1Y1
= 3.0 m/s = V1Y1
From equation
V = V1 + 2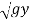 - 2
- 2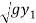
V2 = 4.0 + 2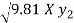 - 2
- 2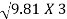
V2 = 6.2642 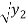 - 6.849
- 6.849
V2Y2 = 3.0
Solving by trial and error:
Y2 = 1.834 m
V2 = 1.635 m/s
Unit 3
Rapidly varied flow
Q1: A stationary hydraulic jump occurs in a rectangular channel with the initial and sequent depth being equal to 0.30 m and 1.20 m respectively. Estimate (i) discharge per unit width (ii) Energy loss.
Solution:

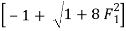
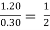
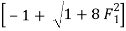
F1 = 3.162
F1 = 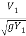 =
= 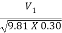 = 3.162
= 3.162
(i) Discharge per unit width q = V1Y1 = 5.424 X 0.30
=1.6272 m3/s/m
(ii) Energy Loss
EL = 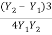 =
= 
EL = 0.506 m
Q2: If in a hydraulic jump occurring in a horizontal rectangular channel, then the Froude number before the jump is 10.0 and the energy loss is 3.10 m. Estimate the sequents depth.
Solution:
The sequent depth ratio
For, F1 = 10
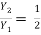
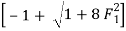
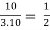
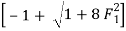
= 13.651
Energy loss
EL = 
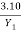 =
= 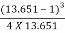
Y1 = Depth before the jump = 0.0836 m
Y2 = Depth after the jump = 1.141 m. Since 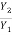 = 13.651
= 13.651
Q3: In a hydraulic jump occurring in a rectangular channel of 3.0 m width, the discharge is 7.8m3/s and the depth before the jump is 0.30 m. Estimate the (i) sequent depths and (ii) the energy loss in the jump.
Solution:
i) V1 = Q/A =  = 8.67 m/s
= 8.67 m/s
F1 = 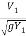 =
= 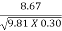 = 5.054
= 5.054
The sequent depth is given by
For F1 = 5.054, 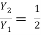
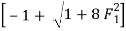
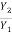 = 6.664
= 6.664
Y2 = 6.664 X 0.03 = 1.99 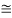 2 m
2 m
Y1 = 0.30 m
Ii) Energy loss
EL = 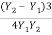
= (2 -3)3 / 4 X 2 X 3
= 2.047 m
Q4: A rectangular channel carrying a supercritical stream is to be provided with a hydraulic jump type of energy dissipater. It is desired to have an energy loss of 4.0 m in the hydraulic jump when the inlet Froude number is 8.5. What are the sequent depths in the jump?
Solution:
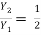
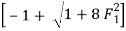
= 
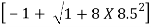
= 11.53
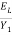 =
= 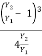
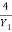 =
= 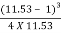
Y1 = 0.158 m
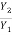 = 11.53
= 11.53
Y2 = 11.53 X 0.158
= 1.822 m
Q5: An overflow spillway is 40.0 m high. At the design energy head of 2.5 m over the spillway. Find the sequent depths. Neglect energy loss due to flow over the spillway face. (Assume Cd = 0.68)
Solution:
q =  Cd
Cd 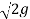 X Hd3/2
X Hd3/2
=  X 6.8 X
X 6.8 X 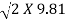 X (2.5)3/2
X (2.5)3/2
= 7.93m3/s/m
By using the equation
P + Hd = Y1 + 
(Energy loss over the spillway is neglected)
Y1 + 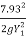 = 42.5
= 42.5
Y1 = 0.28 m
V1 = 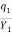 =
= 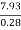 = 28.32 m/s
= 28.32 m/s
F1 = 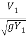 =
= 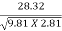
= 17.088
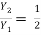
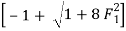
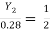
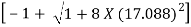
Y2 = 6.627 m
Q6: For a hydraulic jump in a rectangular channel the velocity and depth after the jump are known to be 0.80 m/s and 1.75 m. Calculate the depth before the jump and the energy loss and the power dissipated per meter width.
Solution:
F2 = 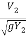 =
= 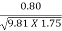 = 0.1931
= 0.1931
The sequent ratio is given in terms of F2 as
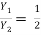
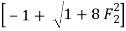
= 
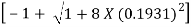
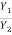 = 0.0697
= 0.0697
Y1 = 0.0697 X 1.75 = 0.122 m
Energy loss,
EL = 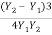
= 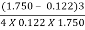
= 5.054 m
The power dissipated, P = 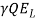
= 9790 X (0.80 – 1.75) X 5.054
= 69270 watt/m width
Q7: A hydraulic jump occurs in a rectangular channel and the depth of flow before and after the jumps are 0.5 and 0.20 m. Calculate the critical depth.
Solution:
Y1 = 0.5 m and Y2 = 0.20 m
The sequent depths are related to critical depth is as follow:
Y1 Y2 (Y1 + Y2) = 2 Yc3
Yc = 0.327 m
Q8: Show that the Froude number F1 and F2 before and after jump respectively, in a hydraulic jump taking place in a rectangular channel are related as:
F22 = 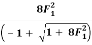
Solution:
F22 = 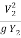 =
= 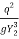
= 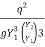 =
= 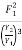
The sequent depth ratio  is related to F1 as
is related to F1 as
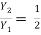
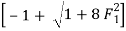
F22 = 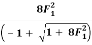
Q9: In a tidal river the depth and velocity of flow are 0.8 m and 1.25 m/s. Due to tidal action, a tidal bore of height 1.2 m is observed to travel upstream. Estimate the height and speed of the bore after the passage of the bore.
Solution: Let Vw (directed downstream) be the velocity of the bore. Superimpose a velocity (-vw) on the system to get stimulated as shown:
Here, Y1 = 0.8m and v1 = 1.25 m/s
Y2 = 0.8 + 1.2 =2.0 m
For positive surge moving in the upstream direction,
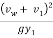 =
=  (
(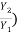 (
(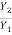 + 1)
+ 1)
(vw + 1.25 )2 = 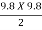 X
X 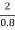 X (
X (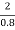 + 1)
+ 1)
Vw = 4.61 m/s
By continuity equation
Y2 (vw + v2) = Y1 (vw + v1)
2 (4.61 + v2) = 0.8 (4.61 + 1.25)
V2 = -2.26 m/s
The river has a velocity of 2.26 m/s directed upstream after the passage of the bore.
Q10: A sluice gate in a wide channel controls the flow of water. When the flow in the downstream channel at a depth of 3.0 m with a velocity of 4.0 m/s. The sluice gate was partially closed, instantaneously to reduce the discharge to 25% of its initial value. Estimate the velocity and depth at the gate.
Solution:
Let suffix 1 refers to the flow condition before the gate closure and suffix 2 conditions after the passage of the negative wave.
Prior velocity, V1 = 4.0 m/s
New discharge intensity, q = 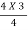 = 3.0 m/s = V1Y1
= 3.0 m/s = V1Y1
From equation
V = V1 + 2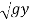 - 2
- 2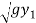
V2 = 4.0 + 2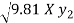 - 2
- 2
V2 = 6.2642 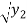 - 6.849
- 6.849
V2Y2 = 3.0
Solving by trial and error:
Y2 = 1.834 m
V2 = 1.635 m/s