Unit 4
Impulse momentum
Q1: Find the force exerted by the jet of water of diameter 745 mm on a stationary flat plate, when the jet strikes the plate normally with a velocity of 20 m/s.
Solution:
Diameter of the jet, d = 75 mm = 0.075 m
Area, a =  d2 =
d2 =  X (0.075)2 = 0.004417 m2
X (0.075)2 = 0.004417 m2
Velocity of the jet, V = 20 m/s
The force exerted by water on a stationary vertical plate is given by equation
F = 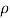 a V2 Where,
a V2 Where, 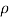 = 1000 kg/m3
= 1000 kg/m3
F = 1000 X 0.004417 X (20)2
F = 1766.8 N
Q2: A jet of water of diameter 75 mm moving with a velocity of 25 m/s strikes a fixed plate in such a way that the angle between and plate is 60 . Find the force exerted by the jet on the plate (i) in the direction normal to the plate and (ii) in the direction of the jet.
. Find the force exerted by the jet on the plate (i) in the direction normal to the plate and (ii) in the direction of the jet.
Solution:
Diameter of the jet, d = 75 mm = 00075 m
Area, a =  d2 =
d2 =  X (0.075)2 = 0.004417 m2
X (0.075)2 = 0.004417 m2
Velocity of the jet, V = 25 m/s
The angle between the jet and plate, 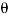 = 60
= 60
(i) The force exerted by the jet of water in the direction normal to the plate is given by equation
Fn = 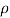 a V2 Sin
a V2 Sin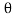
= 1000 X 0.004417 X (25)2 X Sin
= 2390.7 N
(ii) The force in the direction of the jet is given by equation
Fn = 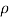 a V2 Sin 2
a V2 Sin 2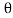
= 1000 X 0.004417 X (25)2 X Sin 2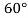
= 2070.4 N
Q3: A jet of water of diameter 75 mm moving with a velocity of 30 m/s, strikes a curved fixed plate tangentially at one end at an angle of 30 to the horizontal. The jet leaves the plate at an angle of 20
to the horizontal. The jet leaves the plate at an angle of 20 to to the horizontal. Find the force exerted by the jet on the plate in the horizontal and vertical directions.
to to the horizontal. Find the force exerted by the jet on the plate in the horizontal and vertical directions.
Solution:
Diameter of the jet, d = 75 mm = 00075 m
Area, a =  d2 =
d2 =  X (0.075)2 = 0.004417 m2
X (0.075)2 = 0.004417 m2
Velocity of the jet, V = 30 m/s
Angle made by the jet at inlet tip with horizontal, 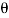 = 30
= 30
Angle made by the jet at outlet tip with horizontal, 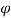 = 20
= 20
The force exerted by the jet of water in the direction of x is given by equation and in the direction of y by equation
Fx = 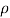 a V2
a V2 
= 1000 X 0.004417  X (30)2
X (30)2
= 7178.2 N
Fy = 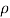 a V2
a V2 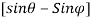
= 1000 X 0.004417  X (30)2
X (30)2
= 628.13 N
Q4: A nozzle of 50 mm diameter delivers a stream of water at 20 m/s perpendiculars to a plate that moves away from the jet at 5 m/s. Find:
(i) The force on the plate.
(ii) The work is done.
(iii) The efficiency of the jet.
Solution:
Diameter of the jet, d = 50 mm = 0.05 m
Area, a =  d2 =
d2 =  X (0.05)2 = 0.0019635 m2
X (0.05)2 = 0.0019635 m2
Velocity of the jet, V = 20 m/s, Velocity of plate, u = 5 m/s
(i) The force on the plate is given by equation
Fx =  a (V-u)2
a (V-u)2
= 1000 X 0.0019635 X (20-5)2
= 441.75 N
(ii) The work done by the jet
Fx X u = 441.78 X 5 = 2208.9 Nm/s
(iii) The efficiency of the jet, n = 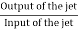
= 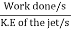 =
= 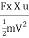
= 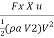
= 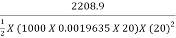
= 0.3377 = 33.77%
Q5: A 7.5 cm diameter jet having a velocity of 30 m/s strikes a flat plate, the normal of which is inclined at 45 to the axis of the jet. Find the normal pressure on the plate: (i) when the plate is stationary, and (ii) when the plate is moving with a velocity of 15 m/s and away from the jet. Also, determine the power and efficiency of the jet when the plate is moving.
to the axis of the jet. Find the normal pressure on the plate: (i) when the plate is stationary, and (ii) when the plate is moving with a velocity of 15 m/s and away from the jet. Also, determine the power and efficiency of the jet when the plate is moving.
Solution:
Given:
Diameter of the jet, d = 75 mm = 00075 m
Area, a =  d2 =
d2 =  X (0.075)2 = 0.004417 m2
X (0.075)2 = 0.004417 m2
Angle between the jet and plate, 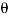 = 90
= 90 - 45
- 45 = 45
= 45
Velocity of the jet, V = 30 m/s
(i) When the plate is stationary, the normal force on the plate is given by equation
Fn = 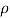 a V2 Sin
a V2 Sin 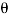
= 1000 X 0.004417 X (30)2 X Sin45
= 2810.96 N
(ii) When the plate is moving with a velocity 15m/s and away fro, the jet, the normal force on the plate is given by
Fn = 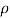 a (V-u)2 Sin
a (V-u)2 Sin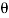
= 1000 X 0.004417 X (30-15)2 X Sin45
= 702.74 N
(iii) The power and efficiency of the jet when plate is moving is obtained by
Work done per second by the jet
= Force in the direction of the jet X Distance moved by the plate in the
direction of the jet/sec
= Fx X u, Where Fx = Fn Sin = 702.74 X Sin45
= 702.74 X Sin45 = 496.9 N
= 496.9 N
Work done/second = 496.9 X 15 = 7453.5 N-m/s
Power in kW = 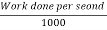 =
= 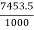 =7.453 kW
=7.453 kW
The efficiency of the jet = 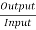 =
= 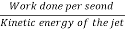
= 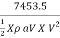
= 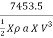
= 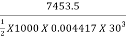
= 0.1249 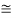 0.125 = 12.5%
0.125 = 12.5%
Q6: A single-acting reciprocating pump, running at 50 r.p.m., delivers 0.01 m3/s of water. The diameter of the piston is 200 mm and the stroke length 400 mm. Determine:
(i) Theoretical discharge of the pump.
(ii) Co-efficient of discharge.
(iii) Slip and the percentage slip of the pump.
Solution:
Speed of the pump, N = 50 r.p.m.
Actual discharge, Qact = 0.01 m3/s
Diameter of piston, D = 200 mm =0.20 m
Area, A =  (0.20)2 = 0.031416 m2
(0.20)2 = 0.031416 m2
Stroke, L = 400 mm 0.40 m
(i) Theoretical discharge for single-acting reciprocating pump is given by equation
Qth = 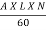 =
= 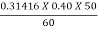 = 0.01047 m3/s
= 0.01047 m3/s
(ii) Co-efficient of discharge is given by
Cd = 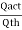 =
= 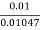 = 0.955
= 0.955
(iii) Slip and the percentage slip of the pump
Slip = Qth - Qact =0.01047 – 0.01 = 0.00047 m3/s
And percentage slip, = 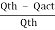 X 100 = (
X 100 = ( 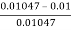 ) X 100
) X 100
= 4.489 %
Q7: The diameters of an impeller of a centrifugal pump at inlet and outlet are 30 cm and 60 cm respectively. Determine the minimum starting speed of the pump if it works against a head of 30 cm.
Solution:
Diameter of impeller at inlet, D1 = 30 cm 0.30 m
Diameter of impeller at outlet, D2 = 60 cm 0.60 m
Head, Hm = 30 cm
Let the minimum starting speed = N
Using the equation for minimum speed,
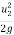 -
- 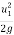 = Hm
= Hm
Where, u2 = 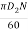 =
= 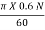 = 0.03141 N
= 0.03141 N
u1 = 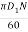 =
=  = 0.0157 N
= 0.0157 N
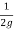 (0.03141N) 2 -
(0.03141N) 2 - 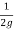 (0.0157N) 2 = 30
(0.0157N) 2 = 30
(0.03141N) 2 - (0.0157N) 2 = 30 X 2 X 9.81
N2 = 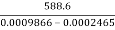 = 795297.9
= 795297.9
N =  = 891.8 r.p.m.
= 891.8 r.p.m.
Q8: The diameters of an impeller of a centrifugal pump at inlet and outlet are 30 cm and 60 cm respectively. The velocity of flow at the outlet is 2.0 m/s and the vanes are set back at an angle of 45 at the outlet. Determine the minimum starting of the pump if the manometric efficiency is 70%.
at the outlet. Determine the minimum starting of the pump if the manometric efficiency is 70%.
Solution:
Diameter of impeller at inlet, D1 = 30 cm 0.30 m
Diameter of impeller at outlet, D2 = 60 cm 0.60 m
Velocity of flow at outlet, Vf2 = 2.0 m/s
Vane angle at outlet,  = 45
= 45
Manometric efficiency, nmax = 70 % =0.70
Let the minimum starting speed = N
From the velocity triangle at the outlet, we have
Tan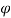 =
= 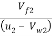
 =
= 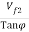
=  = 2.0
= 2.0
Vw2 = u2 – 2.0
U2 = 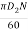 =
= 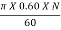 = 0.03141 N
= 0.03141 N
Vw2 = 0.03141N -2.0
For minimum starting speed,
N = 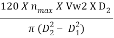 =
= 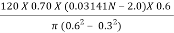
= 59.417 (0.03141 N – 2.0)
= 1.866 N – 118.834
1.866 N – N = 118.934 or 0.886 N = 118.834
N =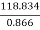 = 137.22 r.p.m.
= 137.22 r.p.m.
Q9: A four-stage centrifugal pump has four identical impellers, keyed to the same shaft. The shaft is running at 400 r.p.m. And the total manometric head developed by the multistage pump is 40 m. The discharge through the pump is 0.2m3/s. The vanes of each impeller are having an outlet angle of 45 . If the width and the diameter of each impeller at the outlet are 5 cm and 60 cm respectively, find the manometric efficiency.
. If the width and the diameter of each impeller at the outlet are 5 cm and 60 cm respectively, find the manometric efficiency.
Solution:
Number of stages, n = 4
Speed, N = 400 r.p.m.
Total manometric head, = 40 m
Manometric head for each stage, Hm = 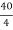 = 10.0 m
= 10.0 m
Discharge, Q = 0.2 m3/s
Outlet vane angle, 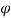 = 45
= 45
Width at outlet, B2 = 5 cm = 0.05 m
Diameter at outlet, D2 = 60 cm = 0.6 m
Tangential velocity of impeller at outlet, u2 = 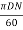 =
= 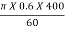 = 12.56 m/s
= 12.56 m/s
Velocity of flow at outlet, Vf2 = 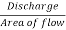 =
= 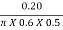 = 20122 m/s
= 20122 m/s
From velocity triangle at outlet,
Tan =
= 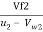
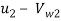 =
= 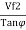 =
= 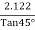 = 2.122 m/s
= 2.122 m/s
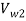 =
= 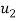 - 2.122 = 12.56 – 2.122 = 10.438
- 2.122 = 12.56 – 2.122 = 10.438
nmax = 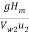 =
= 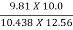 = 0.7482 or 74.82%
= 0.7482 or 74.82%
Q10: Find the number of pumps required to take water from a deep well under a total head of 89 m. All the pumps are identical and are running at 800 r.p.m. The specific speed of each pump is given as 25 while the rated capacity of each pump is 0.16m3/s.
Solution:
Total head, H = 89 m
Speed, N = 800 r.p.m.
Specific speed, Ns = 25
Rate capacity, Q = 0.16 m3/s
Let, Hm = Head developed by each pump.
Ns = 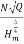
25 = 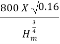
Hm = (12.8)4/3 = 29.94 m
Number of pumps required = 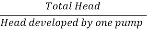 =
= 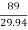 = 3
= 3
Unit 4
Impulse momentum
Q1: Find the force exerted by the jet of water of diameter 745 mm on a stationary flat plate, when the jet strikes the plate normally with a velocity of 20 m/s.
Solution:
Diameter of the jet, d = 75 mm = 0.075 m
Area, a =  d2 =
d2 =  X (0.075)2 = 0.004417 m2
X (0.075)2 = 0.004417 m2
Velocity of the jet, V = 20 m/s
The force exerted by water on a stationary vertical plate is given by equation
F = 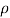 a V2 Where,
a V2 Where, 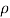 = 1000 kg/m3
= 1000 kg/m3
F = 1000 X 0.004417 X (20)2
F = 1766.8 N
Q2: A jet of water of diameter 75 mm moving with a velocity of 25 m/s strikes a fixed plate in such a way that the angle between and plate is 60 . Find the force exerted by the jet on the plate (i) in the direction normal to the plate and (ii) in the direction of the jet.
. Find the force exerted by the jet on the plate (i) in the direction normal to the plate and (ii) in the direction of the jet.
Solution:
Diameter of the jet, d = 75 mm = 00075 m
Area, a =  d2 =
d2 =  X (0.075)2 = 0.004417 m2
X (0.075)2 = 0.004417 m2
Velocity of the jet, V = 25 m/s
The angle between the jet and plate, 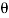 = 60
= 60
(i) The force exerted by the jet of water in the direction normal to the plate is given by equation
Fn =  a V2 Sin
a V2 Sin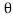
= 1000 X 0.004417 X (25)2 X Sin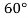
= 2390.7 N
(ii) The force in the direction of the jet is given by equation
Fn = 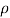 a V2 Sin 2
a V2 Sin 2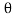
= 1000 X 0.004417 X (25)2 X Sin 2
= 2070.4 N
Q3: A jet of water of diameter 75 mm moving with a velocity of 30 m/s, strikes a curved fixed plate tangentially at one end at an angle of 30 to the horizontal. The jet leaves the plate at an angle of 20
to the horizontal. The jet leaves the plate at an angle of 20 to to the horizontal. Find the force exerted by the jet on the plate in the horizontal and vertical directions.
to to the horizontal. Find the force exerted by the jet on the plate in the horizontal and vertical directions.
Solution:
Diameter of the jet, d = 75 mm = 00075 m
Area, a =  d2 =
d2 =  X (0.075)2 = 0.004417 m2
X (0.075)2 = 0.004417 m2
Velocity of the jet, V = 30 m/s
Angle made by the jet at inlet tip with horizontal,  = 30
= 30
Angle made by the jet at outlet tip with horizontal, 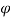 = 20
= 20
The force exerted by the jet of water in the direction of x is given by equation and in the direction of y by equation
Fx = 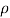 a V2
a V2 
= 1000 X 0.004417  X (30)2
X (30)2
= 7178.2 N
Fy = 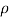 a V2
a V2 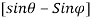
= 1000 X 0.004417  X (30)2
X (30)2
= 628.13 N
Q4: A nozzle of 50 mm diameter delivers a stream of water at 20 m/s perpendiculars to a plate that moves away from the jet at 5 m/s. Find:
(i) The force on the plate.
(ii) The work is done.
(iii) The efficiency of the jet.
Solution:
Diameter of the jet, d = 50 mm = 0.05 m
Area, a =  d2 =
d2 =  X (0.05)2 = 0.0019635 m2
X (0.05)2 = 0.0019635 m2
Velocity of the jet, V = 20 m/s, Velocity of plate, u = 5 m/s
(i) The force on the plate is given by equation
Fx = 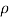 a (V-u)2
a (V-u)2
= 1000 X 0.0019635 X (20-5)2
= 441.75 N
(ii) The work done by the jet
Fx X u = 441.78 X 5 = 2208.9 Nm/s
(iii) The efficiency of the jet, n = 
= 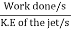 =
= 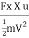
= 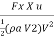
= 
= 0.3377 = 33.77%
Q5: A 7.5 cm diameter jet having a velocity of 30 m/s strikes a flat plate, the normal of which is inclined at 45 to the axis of the jet. Find the normal pressure on the plate: (i) when the plate is stationary, and (ii) when the plate is moving with a velocity of 15 m/s and away from the jet. Also, determine the power and efficiency of the jet when the plate is moving.
to the axis of the jet. Find the normal pressure on the plate: (i) when the plate is stationary, and (ii) when the plate is moving with a velocity of 15 m/s and away from the jet. Also, determine the power and efficiency of the jet when the plate is moving.
Solution:
Given:
Diameter of the jet, d = 75 mm = 00075 m
Area, a =  d2 =
d2 =  X (0.075)2 = 0.004417 m2
X (0.075)2 = 0.004417 m2
Angle between the jet and plate, 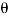 = 90
= 90 - 45
- 45 = 45
= 45
Velocity of the jet, V = 30 m/s
(i) When the plate is stationary, the normal force on the plate is given by equation
Fn = 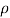 a V2 Sin
a V2 Sin 
= 1000 X 0.004417 X (30)2 X Sin45
= 2810.96 N
(ii) When the plate is moving with a velocity 15m/s and away fro, the jet, the normal force on the plate is given by
Fn = 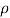 a (V-u)2 Sin
a (V-u)2 Sin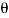
= 1000 X 0.004417 X (30-15)2 X Sin45
= 702.74 N
(iii) The power and efficiency of the jet when plate is moving is obtained by
Work done per second by the jet
= Force in the direction of the jet X Distance moved by the plate in the
direction of the jet/sec
= Fx X u, Where Fx = Fn Sin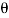 = 702.74 X Sin45
= 702.74 X Sin45 = 496.9 N
= 496.9 N
Work done/second = 496.9 X 15 = 7453.5 N-m/s
Power in kW = 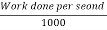 =
= 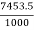 =7.453 kW
=7.453 kW
The efficiency of the jet = 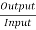 =
= 
= 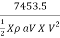
= 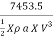
= 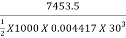
= 0.1249 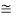 0.125 = 12.5%
0.125 = 12.5%
Q6: A single-acting reciprocating pump, running at 50 r.p.m., delivers 0.01 m3/s of water. The diameter of the piston is 200 mm and the stroke length 400 mm. Determine:
(i) Theoretical discharge of the pump.
(ii) Co-efficient of discharge.
(iii) Slip and the percentage slip of the pump.
Solution:
Speed of the pump, N = 50 r.p.m.
Actual discharge, Qact = 0.01 m3/s
Diameter of piston, D = 200 mm =0.20 m
Area, A =  (0.20)2 = 0.031416 m2
(0.20)2 = 0.031416 m2
Stroke, L = 400 mm 0.40 m
(i) Theoretical discharge for single-acting reciprocating pump is given by equation
Qth =  =
= 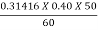 = 0.01047 m3/s
= 0.01047 m3/s
(ii) Co-efficient of discharge is given by
Cd =  =
= 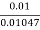 = 0.955
= 0.955
(iii) Slip and the percentage slip of the pump
Slip = Qth - Qact =0.01047 – 0.01 = 0.00047 m3/s
And percentage slip, = 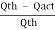 X 100 = (
X 100 = (  ) X 100
) X 100
= 4.489 %
Q7: The diameters of an impeller of a centrifugal pump at inlet and outlet are 30 cm and 60 cm respectively. Determine the minimum starting speed of the pump if it works against a head of 30 cm.
Solution:
Diameter of impeller at inlet, D1 = 30 cm 0.30 m
Diameter of impeller at outlet, D2 = 60 cm 0.60 m
Head, Hm = 30 cm
Let the minimum starting speed = N
Using the equation for minimum speed,
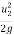 -
- 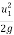 = Hm
= Hm
Where, u2 = 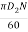 =
= 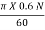 = 0.03141 N
= 0.03141 N
u1 = 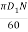 =
= 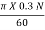 = 0.0157 N
= 0.0157 N
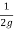 (0.03141N) 2 -
(0.03141N) 2 - 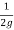 (0.0157N) 2 = 30
(0.0157N) 2 = 30
(0.03141N) 2 - (0.0157N) 2 = 30 X 2 X 9.81
N2 = 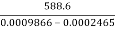 = 795297.9
= 795297.9
N = 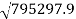 = 891.8 r.p.m.
= 891.8 r.p.m.
Q8: The diameters of an impeller of a centrifugal pump at inlet and outlet are 30 cm and 60 cm respectively. The velocity of flow at the outlet is 2.0 m/s and the vanes are set back at an angle of 45 at the outlet. Determine the minimum starting of the pump if the manometric efficiency is 70%.
at the outlet. Determine the minimum starting of the pump if the manometric efficiency is 70%.
Solution:
Diameter of impeller at inlet, D1 = 30 cm 0.30 m
Diameter of impeller at outlet, D2 = 60 cm 0.60 m
Velocity of flow at outlet, Vf2 = 2.0 m/s
Vane angle at outlet, 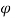 = 45
= 45
Manometric efficiency, nmax = 70 % =0.70
Let the minimum starting speed = N
From the velocity triangle at the outlet, we have
Tan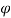 =
= 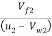
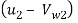 =
= 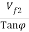
= 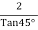 = 2.0
= 2.0
Vw2 = u2 – 2.0
U2 = 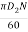 =
= 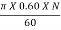 = 0.03141 N
= 0.03141 N
Vw2 = 0.03141N -2.0
For minimum starting speed,
N = 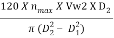 =
= 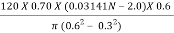
= 59.417 (0.03141 N – 2.0)
= 1.866 N – 118.834
1.866 N – N = 118.934 or 0.886 N = 118.834
N =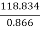 = 137.22 r.p.m.
= 137.22 r.p.m.
Q9: A four-stage centrifugal pump has four identical impellers, keyed to the same shaft. The shaft is running at 400 r.p.m. And the total manometric head developed by the multistage pump is 40 m. The discharge through the pump is 0.2m3/s. The vanes of each impeller are having an outlet angle of 45 . If the width and the diameter of each impeller at the outlet are 5 cm and 60 cm respectively, find the manometric efficiency.
. If the width and the diameter of each impeller at the outlet are 5 cm and 60 cm respectively, find the manometric efficiency.
Solution:
Number of stages, n = 4
Speed, N = 400 r.p.m.
Total manometric head, = 40 m
Manometric head for each stage, Hm =  = 10.0 m
= 10.0 m
Discharge, Q = 0.2 m3/s
Outlet vane angle, 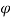 = 45
= 45
Width at outlet, B2 = 5 cm = 0.05 m
Diameter at outlet, D2 = 60 cm = 0.6 m
Tangential velocity of impeller at outlet, u2 = 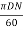 =
=  = 12.56 m/s
= 12.56 m/s
Velocity of flow at outlet, Vf2 = 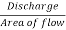 =
= 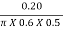 = 20122 m/s
= 20122 m/s
From velocity triangle at outlet,
Tan =
= 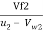
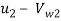 =
=  =
= 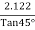 = 2.122 m/s
= 2.122 m/s
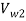 =
= 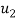 - 2.122 = 12.56 – 2.122 = 10.438
- 2.122 = 12.56 – 2.122 = 10.438
nmax = 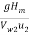 =
= 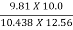 = 0.7482 or 74.82%
= 0.7482 or 74.82%
Q10: Find the number of pumps required to take water from a deep well under a total head of 89 m. All the pumps are identical and are running at 800 r.p.m. The specific speed of each pump is given as 25 while the rated capacity of each pump is 0.16m3/s.
Solution:
Total head, H = 89 m
Speed, N = 800 r.p.m.
Specific speed, Ns = 25
Rate capacity, Q = 0.16 m3/s
Let, Hm = Head developed by each pump.
Ns = 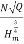
25 = 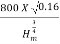
Hm = (12.8)4/3 = 29.94 m
Number of pumps required = 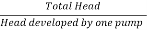 =
= 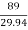 = 3
= 3