UNIT 5
Rotodynamic Machine
Q1: A Pelton wheel has a mean bucket speed of 10m/s with a jet of water flowing at the rate of 700ltr/s under a head i=of 30 m. The buckets deflect the jet through an angle of 160 . Calculate the power given by water to the runner and the hydraulic efficiency of the turbine. Assume co-efficient of velocity as 0.98.
. Calculate the power given by water to the runner and the hydraulic efficiency of the turbine. Assume co-efficient of velocity as 0.98.
Solution:
Speed of bucket, u = u1 = u2 =10m/s
Discharge, Q = 700ltr/s = 0.7 m3/s
Head of water, H = 30m
Angle of discharge, = 160
Angle,  = 180
= 180 - 160
- 160 = 20
= 20
Co-efficient of velocity, Cv = 0.98
The velocity of jet, V1 = Cv 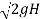 = 0.98 X
= 0.98 X 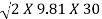
= 23.77 m/s
Vr1 = V1 – u1 = 23.77 – 10
= 13.77 m/s
Vw1 = V1 = 23.77 m/s
From outlet velocity triangle,
Vr2 = Vr1 = 13.77 m/s
Vw2 = Vr2 Cos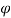 - u2
- u2
= 13.77 Cos20 - 10 = 2.94 m/s
- 10 = 2.94 m/s
Work done by the jet per second on the runner is given by equation as
= 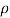 a V1 (Vw1 + Vw2) X u
a V1 (Vw1 + Vw2) X u
= 1000 X 0.7 X (23.77 + 2.94) X 10
= 186970N-m/s
Power given to turbine = 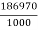 = 18697 kW
= 18697 kW
The hydraulic efficiency of the turbine id given by equation as
nh = 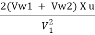 =
= 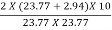
= 0.9454 or 94.54%
Q2: A Pelton wheel is having a mean bucket diameter of 1m and is running at 1000 r.p.m. The net head on the Pelton wheel is 700m. If the side clearance angle is 15 and discharge through nozzle is 0.1m3/s, find:
and discharge through nozzle is 0.1m3/s, find:
(i) Power available at the nozzle and
(ii) Hydraulic efficiency of the turbine.
Solution:
Diameter of wheel, D = 1.0 m
Speed of wheel, N = 1000 r.p.m.
Tangential velocity of the wheel,
u =  =
= 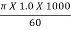
= 52.36 m/s
Net head on turbine, H = 700 m
Side clearance angle, 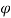 = 15
= 15
Discharge, Q = 0.1 m3/s
Velocity of jet at an inlet, V1 = Cv 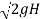 = 1 X
= 1 X 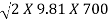
V1 = 117.19 m/s
(i) Power available at the nozzle is given by equation as
W.P = 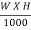 =
= 
= 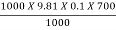
= 686.7 kW
(ii) Hydraulic efficiency is given by equation as
nh = 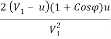
= 
= 0.9718 = 97.18%
Q3: Two jets strike the buckets of a Pelton wheel. Which is having shaft power as 15450kW? The diameter of each jet is given as 200 mm. If the net head on the turbine is 400 m, find the overall efficiency of the turbine. Take Cv = 1.0.
Solution:
Number of jets = 2
Shaft power, S.P = 15450kW
Diameter of each jet, d = 200 mm = 0.20 m
Area of each jet, a =  d2 =
d2 =  X (0.2)2 = 0.031416 m2
X (0.2)2 = 0.031416 m2
Net head, H = 400 m
Co-efficient of velocity, Cv = 1.0
Velocity of each jet, V1 = Cv 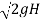 = 1 X
= 1 X 
= 88.58m3/s
Discharge of each jet, = a X V1 = 0.31416 X 88.58
= 2.78m3/s
Total discharge, Q = 2 X 2.78 = 5.56 m2/s
Power of the inlet of turbine,
W.P = 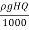 =
= 
= 21817.44 kW
Overall efficiency is given as
n0 = 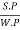 =
=  = 0.708 =70.8%
= 0.708 =70.8%
Q4: The following data is related to a Pelton wheel:
Head at the base of the nozzle = 80 m
Diameter of the jet = 100 mm
Discharge of the nozzle = 0.30 m3/s
Power at the shaft = 206kW
Power absorbed in mechanical resistance = 4.5kW
Determine (i) Power lost in nozzle and (ii) Power lost due to hydraulic resistance in the runner.
Solution:
Head at the base of the nozzle,
H1 = 80m
Diameter of the jet, d = 100 mm = 0.1 m
Area of the jet, a =  d2 =
d2 =  X (0.1)2 = 0.007854 m2
X (0.1)2 = 0.007854 m2
Discharge of the nozzle, Q = 0.30 m3/s
Shaft Power, S.P = 206kW
Power absorbed in mechanical resistance = 4.5kW
Now discharge, Q = Area of jet X velocity of jet = a X V1
0.3 = 0.007854 X V1
V1 = 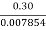 = 38.197 m/s
= 38.197 m/s
Power at the base of the nozzle in kW
= 
= 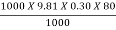
= 235.44kW
Power corresponding to kinetic energy of the jet in kW
 X
X 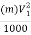 =
=  X
X  =
=  X
X 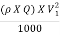
=  X
X 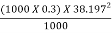
= 218.85 kW
(i) Power at thy base of the nozzle = power of the jet + Power lost in nozzle
235.44 = 218.44 – 218.85 = 16.59kW
(ii) Also power at the base of nozzle = Power at the shaft + Power lost in nozzle + Power lost on runner + Power lost due to mechanical resistance
235.44 = 206 +16.59 + Power lost in runner + 4.5
Power lost in runner = 235.44 -227.09 = 8.53 kW
Q5: A centrifugal pump delivers water against a net head of 14.5 m and a design speed of 900 r.p.m. The vanes are curved back to an angle of 30 with the periphery. The impeller diameter is 300 mm and outlet width is 50 mm. Determine the discharge of the pump id manometric efficiency is 95%.
with the periphery. The impeller diameter is 300 mm and outlet width is 50 mm. Determine the discharge of the pump id manometric efficiency is 95%.
Solution:
Net Head, H = 14.5 m
Speed, N = 900 r.p.m.
Vane angle at outlet, 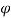 = 30
= 30
Impeller diameter means the diameter of the impeller at outlet.
Diameter, D2 = 300 mm = 0.30 m
Outlet width, B2 = 50 mm = 0.05 m
Manometric efficiency, nmax = 95% = 0.95
Tangential velocity of impeller at outlet,
U2 = 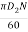 =
= 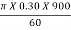
= 14.14 m/s
Now using equation,
nmax = 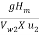
0.95 = 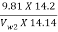
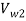 = 10.6 m/s
= 10.6 m/s
From outlet triangle, we have
tan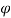 =
= 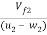
tan30 =
= 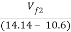 =
= 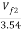
Vf2 = 2.04 m/s
Discharge, Q = 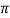 D2B2 X Vf2
D2B2 X Vf2
Q = 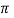 X 0.30 X 0.05 X 2.04
X 0.30 X 0.05 X 2.04
Q = 0.1 m3/s
Q6: Find the power required to drive a centrifugal pump which delivers 0.04 m3/s of water to a height a 15 cm diameter pipe and 100 m long. The overall efficiency of the pump is 70% and co-efficient of friction ‘f’ = 0.15 in the formula .
.
Solution:
Discharge, Q = 0.04 m3/s
Height, Hs = hs + hd =20 m
Diameter of pipe, Ds = Dd =15 cm = 0.15 m
Length, L = Ls + Ld = 70% = 0.70
Co-efficient of friction, f = 0.015
Velocity of water in pipe, Vs = Vd =V = 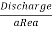
= 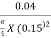 = 2.26 m/s
= 2.26 m/s
Frictional head loss in pipe,
(hfs + hfd) = 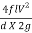 =
= 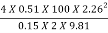
= 1041 m
Using equation, we get manometric head as
Hm = (hs + hd) + (hfs + hfd) + 
= 20 + 10.41 + 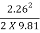 = 30.67 m
= 30.67 m
Overall efficiency is given by equation as
no = 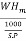 =
= 
S.P = 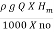
S.P = 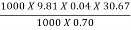 = 17.19kW
= 17.19kW
S.P is the power required to drive the centrifugal pump.
Q7: Find the number of pumps required to take water from a deep well under a total head of 89.82 m. All the pumps are identical and are running at 800 r.p.m. The specific speed of each pump is given as 25 while the rated capacity of each pump is 0.16m3/s.
Solution:
Total head, H = 89 m
Speed, N = 800 r.p.m.
Specific speed, Ns = 25
Rate capacity, Q = 0.16 m3/s
Let, Hm = Head developed by each pump
Using equation,
Ns = 
25 = 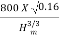
Hm3/4 =  = 12.8
= 12.8
Hm = 29.94 m
Number of pumps required = 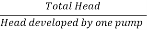
= 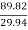
= 3
As the total head is more than the head developed by one pump, the pumps should be connected in series.
Q8: An inward flow reaction turbine has external and internal diameters as 1 m and 0.5 m respectively. The velocity of flow through the runner is constant and is equal to 1.5 m/s. Determine
(i) Discharge through the runner, and
(ii) Width of the turbine at outlet if the width of the turbine at inlet = 200 mm.
Solution:
External diameter of turbines, D1 = 1 m
Internal diameters of turbine, D2 = 0.5 m
Velocity of flow at inlet and outlet,
Vf1 = Vf2 = 1.5 m/s
Width of turbine at inlet,
B1 = 200 mm = 0.20m
Let the width at outlet = B2
Using equation for discharge,
Q = 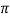 D1 B1 X Vf1 =
D1 B1 X Vf1 = 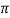 X 1 X 0.20 X 1.5
X 1 X 0.20 X 1.5
= 0.9425 m3/s
Also, 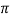 D1 B1 X Vf1 =
D1 B1 X Vf1 = 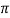 D2 B2 X Vf2
D2 B2 X Vf2
Or, D1 B1 = D2 B2
B2 = 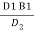 =
= = 0.40 m
= 0.40 m
Q9: A turbine is to operate under a head of 25 m at 200 r.p.m. The discharge is 9cumec. If the efficiency is 90% determine:
(i) Specific speed of the machine.
(ii) Power generated and
(iii) Type of turbine.
Solution:
Head, H = 25 m
Speed, N = 200 r.p.m.
Discharge, Q = 9 cumec = 9 m3/s
Efficiency, no = 90% 0.90
Now using relation, no = 
= 
P = no X 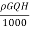
P = 0.90 X 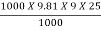
P = 1986.5 kW
(i) Specific speed of the turbine (Ns)
Using equation, Ns =  =
= 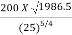
= 159.46 r.p.m.
(ii) Power generated, P = 1986.5 kW
(iii) As the specific speed lies between 51 and 255, the turbine is a Francis turbine.
Q10: A turbine develops 9000 kW when running at a speed of r.p.m. And under a head of 30 m. Determine the specific speed of the turbine.
Solution:
Power developed, P = 9000 kW
Head, H = 30 m
Speed, N = 140 r.p.m.
The specific speed is given by equation as
Ns = 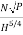 =
= 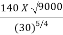
Ns = 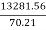
Ns = 189.167 (S.I. Units).
UNIT 5
Rotodynamic Machine
Q1: A Pelton wheel has a mean bucket speed of 10m/s with a jet of water flowing at the rate of 700ltr/s under a head i=of 30 m. The buckets deflect the jet through an angle of 160 . Calculate the power given by water to the runner and the hydraulic efficiency of the turbine. Assume co-efficient of velocity as 0.98.
. Calculate the power given by water to the runner and the hydraulic efficiency of the turbine. Assume co-efficient of velocity as 0.98.
Solution:
Speed of bucket, u = u1 = u2 =10m/s
Discharge, Q = 700ltr/s = 0.7 m3/s
Head of water, H = 30m
Angle of discharge, = 160
Angle,  = 180
= 180 - 160
- 160 = 20
= 20
Co-efficient of velocity, Cv = 0.98
The velocity of jet, V1 = Cv 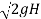 = 0.98 X
= 0.98 X 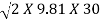
= 23.77 m/s
Vr1 = V1 – u1 = 23.77 – 10
= 13.77 m/s
Vw1 = V1 = 23.77 m/s
From outlet velocity triangle,
Vr2 = Vr1 = 13.77 m/s
Vw2 = Vr2 Cos - u2
- u2
= 13.77 Cos20 - 10 = 2.94 m/s
- 10 = 2.94 m/s
Work done by the jet per second on the runner is given by equation as
= 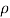 a V1 (Vw1 + Vw2) X u
a V1 (Vw1 + Vw2) X u
= 1000 X 0.7 X (23.77 + 2.94) X 10
= 186970N-m/s
Power given to turbine = 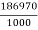 = 18697 kW
= 18697 kW
The hydraulic efficiency of the turbine id given by equation as
nh = 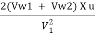 =
= 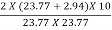
= 0.9454 or 94.54%
Q2: A Pelton wheel is having a mean bucket diameter of 1m and is running at 1000 r.p.m. The net head on the Pelton wheel is 700m. If the side clearance angle is 15 and discharge through nozzle is 0.1m3/s, find:
and discharge through nozzle is 0.1m3/s, find:
(i) Power available at the nozzle and
(ii) Hydraulic efficiency of the turbine.
Solution:
Diameter of wheel, D = 1.0 m
Speed of wheel, N = 1000 r.p.m.
Tangential velocity of the wheel,
u = 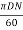 =
= 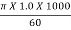
= 52.36 m/s
Net head on turbine, H = 700 m
Side clearance angle,  = 15
= 15
Discharge, Q = 0.1 m3/s
Velocity of jet at an inlet, V1 = Cv  = 1 X
= 1 X 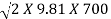
V1 = 117.19 m/s
(i) Power available at the nozzle is given by equation as
W.P =  =
= 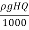
= 
= 686.7 kW
(ii) Hydraulic efficiency is given by equation as
nh = 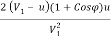
= 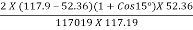
= 0.9718 = 97.18%
Q3: Two jets strike the buckets of a Pelton wheel. Which is having shaft power as 15450kW? The diameter of each jet is given as 200 mm. If the net head on the turbine is 400 m, find the overall efficiency of the turbine. Take Cv = 1.0.
Solution:
Number of jets = 2
Shaft power, S.P = 15450kW
Diameter of each jet, d = 200 mm = 0.20 m
Area of each jet, a =  d2 =
d2 =  X (0.2)2 = 0.031416 m2
X (0.2)2 = 0.031416 m2
Net head, H = 400 m
Co-efficient of velocity, Cv = 1.0
Velocity of each jet, V1 = Cv 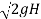 = 1 X
= 1 X 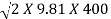
= 88.58m3/s
Discharge of each jet, = a X V1 = 0.31416 X 88.58
= 2.78m3/s
Total discharge, Q = 2 X 2.78 = 5.56 m2/s
Power of the inlet of turbine,
W.P = 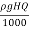 =
= 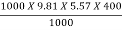
= 21817.44 kW
Overall efficiency is given as
n0 = 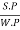 =
= 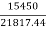 = 0.708 =70.8%
= 0.708 =70.8%
Q4: The following data is related to a Pelton wheel:
Head at the base of the nozzle = 80 m
Diameter of the jet = 100 mm
Discharge of the nozzle = 0.30 m3/s
Power at the shaft = 206kW
Power absorbed in mechanical resistance = 4.5kW
Determine (i) Power lost in nozzle and (ii) Power lost due to hydraulic resistance in the runner.
Solution:
Head at the base of the nozzle,
H1 = 80m
Diameter of the jet, d = 100 mm = 0.1 m
Area of the jet, a =  d2 =
d2 =  X (0.1)2 = 0.007854 m2
X (0.1)2 = 0.007854 m2
Discharge of the nozzle, Q = 0.30 m3/s
Shaft Power, S.P = 206kW
Power absorbed in mechanical resistance = 4.5kW
Now discharge, Q = Area of jet X velocity of jet = a X V1
0.3 = 0.007854 X V1
V1 = 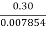 = 38.197 m/s
= 38.197 m/s
Power at the base of the nozzle in kW
= 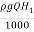
= 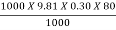
= 235.44kW
Power corresponding to kinetic energy of the jet in kW
 X
X 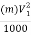 =
=  X
X 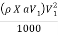 =
=  X
X 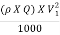
=  X
X 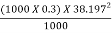
= 218.85 kW
(i) Power at thy base of the nozzle = power of the jet + Power lost in nozzle
235.44 = 218.44 – 218.85 = 16.59kW
(ii) Also power at the base of nozzle = Power at the shaft + Power lost in nozzle + Power lost on runner + Power lost due to mechanical resistance
235.44 = 206 +16.59 + Power lost in runner + 4.5
Power lost in runner = 235.44 -227.09 = 8.53 kW
Q5: A centrifugal pump delivers water against a net head of 14.5 m and a design speed of 900 r.p.m. The vanes are curved back to an angle of 30 with the periphery. The impeller diameter is 300 mm and outlet width is 50 mm. Determine the discharge of the pump id manometric efficiency is 95%.
with the periphery. The impeller diameter is 300 mm and outlet width is 50 mm. Determine the discharge of the pump id manometric efficiency is 95%.
Solution:
Net Head, H = 14.5 m
Speed, N = 900 r.p.m.
Vane angle at outlet, 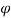 = 30
= 30
Impeller diameter means the diameter of the impeller at outlet.
Diameter, D2 = 300 mm = 0.30 m
Outlet width, B2 = 50 mm = 0.05 m
Manometric efficiency, nmax = 95% = 0.95
Tangential velocity of impeller at outlet,
U2 =  =
= 
= 14.14 m/s
Now using equation,
nmax = 
0.95 = 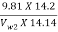
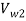 = 10.6 m/s
= 10.6 m/s
From outlet triangle, we have
tan =
= 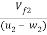
tan30 =
= 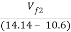 =
= 
Vf2 = 2.04 m/s
Discharge, Q = 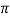 D2B2 X Vf2
D2B2 X Vf2
Q = 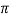 X 0.30 X 0.05 X 2.04
X 0.30 X 0.05 X 2.04
Q = 0.1 m3/s
Q6: Find the power required to drive a centrifugal pump which delivers 0.04 m3/s of water to a height a 15 cm diameter pipe and 100 m long. The overall efficiency of the pump is 70% and co-efficient of friction ‘f’ = 0.15 in the formula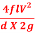 .
.
Solution:
Discharge, Q = 0.04 m3/s
Height, Hs = hs + hd =20 m
Diameter of pipe, Ds = Dd =15 cm = 0.15 m
Length, L = Ls + Ld = 70% = 0.70
Co-efficient of friction, f = 0.015
Velocity of water in pipe, Vs = Vd =V = 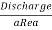
= 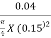 = 2.26 m/s
= 2.26 m/s
Frictional head loss in pipe,
(hfs + hfd) = 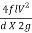 =
= 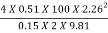
= 1041 m
Using equation, we get manometric head as
Hm = (hs + hd) + (hfs + hfd) + 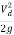
= 20 + 10.41 + 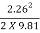 = 30.67 m
= 30.67 m
Overall efficiency is given by equation as
no = 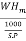 =
= 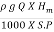
S.P = 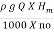
S.P = 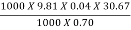 = 17.19kW
= 17.19kW
S.P is the power required to drive the centrifugal pump.
Q7: Find the number of pumps required to take water from a deep well under a total head of 89.82 m. All the pumps are identical and are running at 800 r.p.m. The specific speed of each pump is given as 25 while the rated capacity of each pump is 0.16m3/s.
Solution:
Total head, H = 89 m
Speed, N = 800 r.p.m.
Specific speed, Ns = 25
Rate capacity, Q = 0.16 m3/s
Let, Hm = Head developed by each pump
Using equation,
Ns = 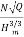
25 = 
Hm3/4 = 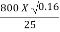 = 12.8
= 12.8
Hm = 29.94 m
Number of pumps required = 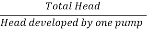
= 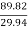
= 3
As the total head is more than the head developed by one pump, the pumps should be connected in series.
Q8: An inward flow reaction turbine has external and internal diameters as 1 m and 0.5 m respectively. The velocity of flow through the runner is constant and is equal to 1.5 m/s. Determine
(i) Discharge through the runner, and
(ii) Width of the turbine at outlet if the width of the turbine at inlet = 200 mm.
Solution:
External diameter of turbines, D1 = 1 m
Internal diameters of turbine, D2 = 0.5 m
Velocity of flow at inlet and outlet,
Vf1 = Vf2 = 1.5 m/s
Width of turbine at inlet,
B1 = 200 mm = 0.20m
Let the width at outlet = B2
Using equation for discharge,
Q = 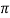 D1 B1 X Vf1 =
D1 B1 X Vf1 = 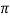 X 1 X 0.20 X 1.5
X 1 X 0.20 X 1.5
= 0.9425 m3/s
Also, 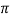 D1 B1 X Vf1 =
D1 B1 X Vf1 = 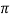 D2 B2 X Vf2
D2 B2 X Vf2
Or, D1 B1 = D2 B2
B2 = 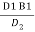 =
=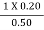 = 0.40 m
= 0.40 m
Q9: A turbine is to operate under a head of 25 m at 200 r.p.m. The discharge is 9cumec. If the efficiency is 90% determine:
(i) Specific speed of the machine.
(ii) Power generated and
(iii) Type of turbine.
Solution:
Head, H = 25 m
Speed, N = 200 r.p.m.
Discharge, Q = 9 cumec = 9 m3/s
Efficiency, no = 90% 0.90
Now using relation, no = 
= 
P = no X 
P = 0.90 X 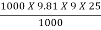
P = 1986.5 kW
(i) Specific speed of the turbine (Ns)
Using equation, Ns = 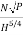 =
= 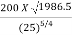
= 159.46 r.p.m.
(ii) Power generated, P = 1986.5 kW
(iii) As the specific speed lies between 51 and 255, the turbine is a Francis turbine.
Q10: A turbine develops 9000 kW when running at a speed of r.p.m. And under a head of 30 m. Determine the specific speed of the turbine.
Solution:
Power developed, P = 9000 kW
Head, H = 30 m
Speed, N = 140 r.p.m.
The specific speed is given by equation as
Ns = 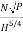 =
= 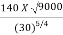
Ns = 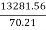
Ns = 189.167 (S.I. Units).