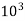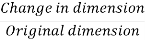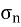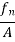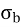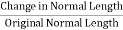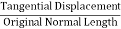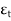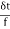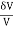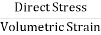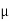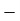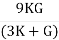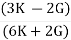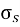Hooke’s Law | unit 1 simple stress and strains

Back to Study material

ISM

Unit – 1Simple Stress and Strains Q1) Explain Stress and Strain in detail.A1)

Stress -

When a material is subjected to an external force, a resisting force is set up in the component.
The internal resistance force per unit area acting on a material is called the stress at a point. It is a tensor quantity having unit of N/m2 or Pascal.

Stress =

Force(F) is expressed in Newton (N)
Original area (A), in square meters (m2)
The stress σ will be expresses in N/m2. This unit is called Pascal (Pa).
As Pascal is a small quantity, in practice, multiples of this unit is used.

1kPa = Pa = N/m2

1MPa = 106Pa = 106N/m2 = 1N/mm2

1GPa = 109Pa = 109N/m2

Strain –

It is the deformation produced in the material due to simple stress.
It usually represents the displacement between particles in the body relative to a reference length.
Strain =

Q2) Explain the types of Stress in detail.A2)

Normal stress

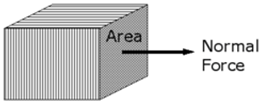
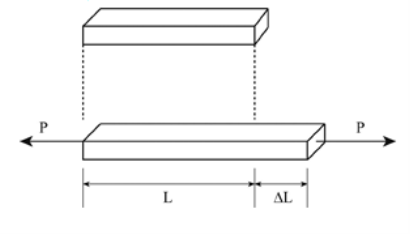
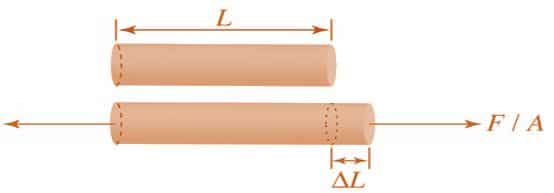
Normal Stress = =

Fig No 1.1 Normal Stress

Shear Stress

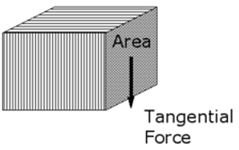
Fig No 1.2 Shear Stress

Bulk Stress

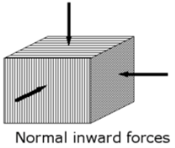
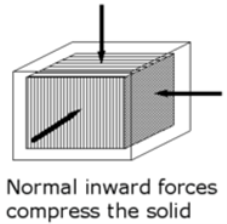
Fig No 1.3 Bulk Stress

Bulk Stress = = P

Q3) Explain the types of Strain in detail.A3) Types of Strain –

Normal Strain:

The normal strain of a body is generally expressed as the ratio of total displacement to the original length.

Normal Strain =

Fig 1.4 Normal Strain

Since strain is m/m, it is dimensionless.

It is of two types: Longitudinal strain and Lateral Strain

The longitudinal strain is defined as the ratio of the change in length of the body due to the deformation to its original length in the direction of the force.

The Lateral Strain is defined as the ratio of the change in length (breadth of a rectangular bar or diameter of a circular bar) of the body due to the deformation to its original length (breadth of a rectangular bar or diameter of a circular bar) in the direction perpendicular to the force.

Poisson’s Ratio ( =

Shear strain

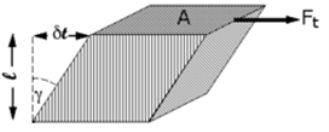
Fig No 1.5 Shear Strain

Note 1: The angle is radians, not degrees. The volume of the solid is not changed by shear strain.

Shear Strain =

= = y (rad)

Bulk Strain or Volumetric Strain

Fig No. 1.6 Volumetric Strain

Bulk Strain =

Q4) Explain the Hooke’s Law in detail.A4)

Hooke’s Law

According to Hook’s law the stress is directly proportional to strain i.e. normal stress (σ) ∝ normal strain (ε) and shearing stress ( ζ )∝ shearing strain ( γ ).

σ = Eε and ζ = γG

The co-efficient E is called the modulus of elasticity i.e. its resistance to elastic strain. The coefficient

G is called the shear modulus of elasticity or modulus of rigidity.

Q5) Explain the Stress-Strain Diagram for Brittle Metal and for Ductile Metal in detail.A5)

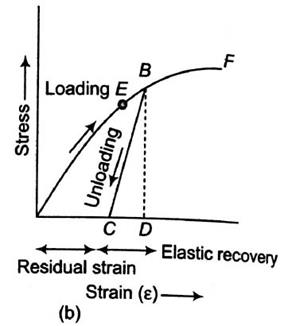
(A) For Brittle Metal –

The stress-strain diagram is shown in the figure. In brittle materials, there is no appreciable change in the rate of strain. There is no yield point and no necking takes place.

Fig No 1.7 Stress-Strain Diagram (Brittle Metal)

In figure (a), the specimen is loaded only up to point A, when load has gradually removed the curve follows the same path AO and strain completely disappears. Such behavior is known as elastic behavior.

In figure (b), the specimen is loaded up to point B beyond the elastic limit E. When the specimen has gradually loaded the curve follows path BC, resulting in a residual strain OC or permanent strain.

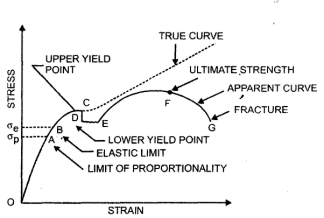
(B) For Ductile Metal –

The true stress-strain curve is also known as the flow curve.

Fig No 1.8 Stress-Strain Diagram (Ductile Metal)

True stress-strain curve gives a true indication of deformation characteristics because it is based on the instantaneous dimension of the specimen.

In engineering stress-strain curve, stress drops down after necking since it is based on the original area.

In true stress-strain curve, the stress, however, increases after necking since the cross-sectional area of the specimen decreases rapidly after necking.

The flow curve of many metals in the region of uniform plastic deformation can be expressed by the simple power law.

σT = K(εT)n

Where K is the strength coefficient

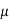n is the strain hardening exponentn = 0 perfectly plastic solidn = 1 elastic solid for most metals, 0.1< n < 0.5 Q6) Explain the Different elastic constants in detail.A6)Different elastic constants are as follows:

Young’s modulus

Bulk modulus

Rigidity modulus

Poisson’s ratio

1. Young’s Modulus

According to Hooke’s law, when a body is subjected to tensile stress or compressive stress, the stress applied is directly proportional to the strain within the elastic limits of that body.

The ratio of applied stress to the strain is constant and is known as Young’s modulus or modulus of elasticity.

Young’s modulus is denoted by letter “E”. The unit of modulus of elasticity is the same as the unit of stress which is mega pascal (mPa). 1 mPa is equal to 1 N/mm2.

Young’s Modulus (E) =

tensile stress

Fig 1.10: Body Subjected to Tensile Stress

2) Bulk Modulus

When a body is subjected to mutually perpendicular direct stresses which are alike and equal, within its elastic limits, the ratio of direct stress to the corresponding volumetric strain is found to be constant.

This ratio is called bulk modulus and is represented by letter “K”. Unit of Bulk modulus is mPa.

Bulk Modulus (K) =

Fig1.11: Volumetric Change of Body

3. Rigidity ModulusWhen a body is subjected to shear stress the shape of the body gets changed, the ratio of shear stress to the corresponding shear strain is called rigidity modulus or modulus of rigidity. It is denoted by the letters “G” or “C” or “N”. Unit of rigidity modulus is mPa.

Rigidity Modulus (G) =

shear deformation

Fig 1.12: Shear Deformation of Body

4. Poisson’s Ratio

When a body is subjected to simple tensile stress within its elastic limits then there is a change in the dimensions of the body in the direction of the load as well as in the opposite direction.

When these changed dimensions are divided with their original dimensions, longitudinal strain and lateral strain are obtained.

The ratio of the lateral strain to the longitudinal strain is called Poisson’s ratio. It is represented by the symbol “µ”. Poisson’s ratio is maximum for an ideal elastic incompressible material and its value is 0.5.

For most of the engineering materials, Poisson’s ratio lies between 0.25 and 0.33. It has no units.

Q7) Explain the relationship between Elastic Constants in detail.A7)

Relationship between Elastic Constants

The relationship between Young’s modulus (E), rigidity modulus (G) and Poisson’s ratio (µ) is expressed as:

E = 2G (1 + )

The relationship between Young’s modulus (E), bulk modulus (K) and Poisson’s ratio (µ) is expressed as:

E = 3K (1 2)

Young’s modulus can be expressed in terms of bulk modulus (K) and rigidity modulus (G) as:

E =

Poisson’s ratio can be expressed in terms of bulk modulus (K) and rigidity modulus (G) as:

E =

Q8) Explain the Strain Energy for Gradually Applied Load, Suddenly Applied Load and Impact Load in detail.A8)

Strain Energy for Gradually Applied Load, Suddenly Applied Load and Impact Load.

Application of external loads to a member causes deformation of the member but the member has a natural tendency to oppose the deformation and in doing so it develops internal stresses.

These internal stresses have the capacity to do work and as such, the member has energy stored in it. Thus work done upon a member in straining it is called as Strain Energy.

Volume of bar= A.L Strain Energy when loading is gradually applied load to the member.

(A) Gradually Applied load –

Let us consider a vertical bar of X-sectional area 'A' be rigidly held at one end and carry a gradually applied load at the other end as shown in fig.

Let δl be extension in length L

enter image description here

Fig No 1.16 Gradually Applied Load

Strain energy stored in the member=world done by gradually applied load.

Strain energy when loading is suddenly applied load to the member

(B) Suddenly Applied Load –

Let the load P be suddenly applied. Let the extension of member be δl.

In this case, the magnitude of load is constant throughout the process of extension.

Let 'p' be the maximum stress included. Equating strain energy stored by the member to the work done.

Hence, the maximum stress intensity due to a suddenly applied load is twice the stress intensity produced by the load of the same magnitude applied gradually.

Strain Energy when loading is impacted load to the member.

In this case, the load P is dropped from a height h before it commences to stretch the bar.

A vertical bar whose upper end is fixed at the top and collar is provided at the lower end.

Load P drops by a height h on the collar and this extend the member by δl

Let p=maximum stress intensity produced in the bar/ Hence extension at bar

Q9) Explain the formula and definition of Shear Stress and Shear StrainA9)

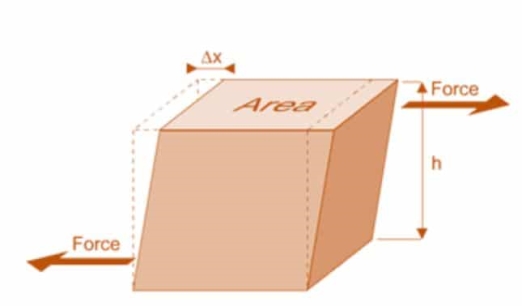
Shear Stress –

The shear stress is defined to be the ratio of the tangential force to the cross sectional area of the surface upon which it acts,

= F tan / A

b) Shear Strain –

The shear strain is defined to be the ratio of the horizontal displacement to the height of the block,

α = δ x / h

Q10) Explain the Mohr’s Stress Circle in details.A10) Mohr’s Stress Circle

Mohr's circle is a geometric representation of the two-dimensional stress state and is very useful to perform quick and efficient estimations.

It is also popularly used in geotechnical fields such as soil strength, stress path, earth pressure and bearing capacity. It is often used to interpret the test data, to analyze complex geotechnical problems, and to predict soil behavior.

The pole point on Mohr's circle is a point so special that it can help to readily find stresses on any specified plane by using diagram instead of complicated computation.

There will be one plane on which normal stress value is maximum, this plane is known as Principal plane (more precisely maximum principal plane) and normal stress on this plane is known as principal stress (more precisely maximum principal stress). Similarly, there will be one more plane on which normal stress value is minimum, this is also a principal plane (minimum principal plane) and normal stress on this plane is known as Principal stress (minimum principal stress).

Starting with a stress or strain element in the XY plane, construct a grid with a normal stress on the horizontal axis and a shear stress on the vertical. (Positive shear stress plots at the bottom.) Then just follow these steps:

Plot the vertical face coordinates V (σxx , τxy).

Plot the horizontal coordinates H (σyy, –τxy).

Draw a diameter line connecting Points V (from Step1) and H (from Step2).

Sketch the circle around the diameter from Step 3.

Compute the normal stress position for the circle’s center point (C).

Calculate the radius (R) for the circle.

Determine the principal stresses σP1 and σP2.

Compute the principal angles ΘP1 and ΘP2.

Q11) Explain the Theories of Failure in details.A11)Theories of Failure

When a machine element is subjected to a system of complex stress system, it is important to predict the mode of failure so that the design methodology may be based on a particular failure criterion. Theories of failure are essentially a set of failure criteria developed for the ease of design.

In machine design an element is said to have failed if it ceases to perform its function. There are basically two types of mechanical failure:

1. Yielding- This is due to excessive inelastic deformation rendering the machine part unsuitable to perform its function. This mostly occurs in ductile materials. 2. Fracture- in this case the component tears apart in two or more parts. This mostly occurs in brittle materials.

There are many instances when a ductile material may fail by fracture. This may occur if a material is subjected to

(a) Cyclic loading (b) Long term static loading at elevated temperature (c) Impact loading (d) Work hardening (e) Severe quenching

Sign Up