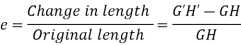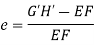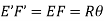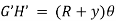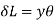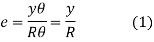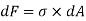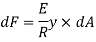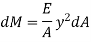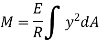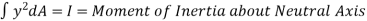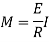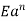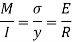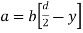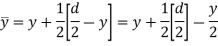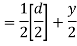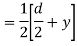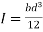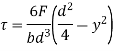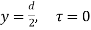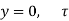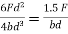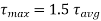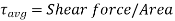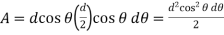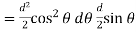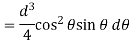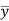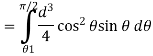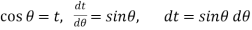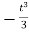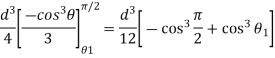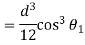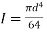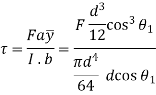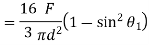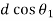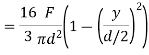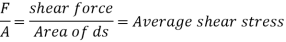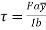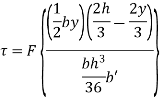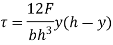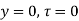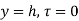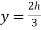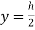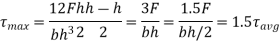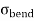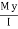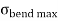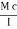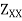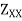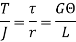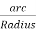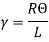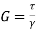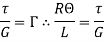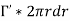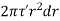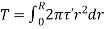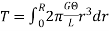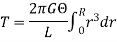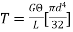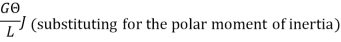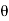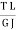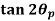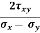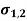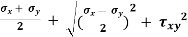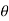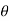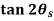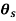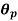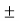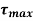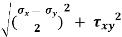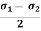Theory of Simple Bending | unit 3 flexural stresses and torsions

ISM

Unit – 3Flexural Stresses Q1) Explain in detail Theory of Simple Bending.A1)

Pure bending (Theory of simple bending) is a condition of stress where a bending moment is applied to a beam without the simultaneous presence of axial, shear, or torsional forces.

Pure bending occurs only under a constant bending moment (M) since the shear force (V), which is equal to

= V, has to be equal to zero.

In reality, a state of pure bending does not practically exist, because such a state needs an absolutely weightless member. The state of pure bending is an approximation made to derive formulas.

Q2) Explain in detail Assumptions of theory of Simple Bending.A2)

Assumptions of theory of Simple Bending –

The material of the beam is homogeneous and isotropic.

The value of Young's Modulus of Elasticity is same in tension and compression.

The transverse sections which were plane before bending, remain plane after bending also.

The beam is initially straight and all longitudinal filaments bend into circular arcs with a common center of curvature.

The radius of curvature is large as compared to the dimensions of the cross-section.

Each layer of the beam is free to expand or contract, independently of the layer, above or below it.

Q3) Explain Derivation of Bending Equation.A3)

Derivation of Flexure formula for pure bending

Fig.1-Before bendingConsider any two normal sections AB and CD of a beam for a small length ‘dx’ apart as shown in fig. After the action of the transverse loading on the beam, the beam will be bends A’B’C’D’ as shown in fig. Below

Fig 2 -After bending

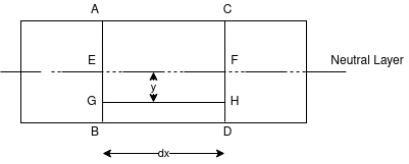
Let A’ B’ and C’ D’ intersect each other at O.

Let, R = Radius of curvature of Neutral layer FF.

Θ = Subtended angle at o

Consider a layer GH at a distance y from Neutral axis

Strain in layer GH due to bending

Let GH=EF

From fig-2

Length of arc = Subtended angle × Radius

Original length

Length of layer

Change in length

By definition, modulus of elasticity

From Equation (1) and (2)

Since E and R are constant, the stress is directly proportional to the distance from Neutral axis.

Now consider cross-section of the beam.

Consider an elemental strip at ‘y’ from NA and Area of strip ‘dA’.

Force on the strip = Stress on the strip × Area on the strip

Moment of this force about N.A

Total moment of whole section about N.A

But Fig. 3

From (3) and (4)

This is known as Bending formula or Flexure formula.

Q4) Explain Shear Stress variation of standard cross sectionsA4)Shear Stress variation of some standard cross sections –A) Rectangular Section

Fig.4 Rectangular SectionConsider a rectangular section of width b and depth d subjected to shearing force F.Let AA be a fibre at a distance y from the NA

Where

And , substituting

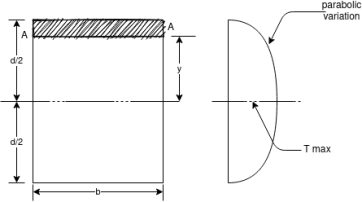
Thus the shear stress variation is parabolic when

(i) at

(ii) at

(iii) is max and its value is

, For a rectangular section and this occurs at the neutral axis, where

B) Circular SectionConsider a circular section of diagram d as shown in fig. Let AA be a fibre at a vertical distance y and angle from NA on which shear stress is to be determined. To find moment of area above the fibre AA about the N.A.Consider an element of thickness dz at a vertical distance z from the N.ALet the angular distance of the element be θArea of element A=b.dx

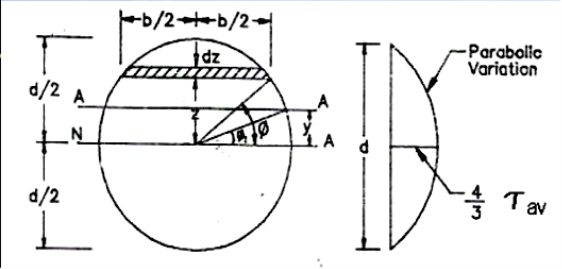
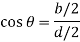Width of the element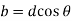

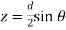
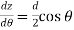
Fig.5 Circular Section

Area of the element

Moment of area of the element about the N.A=A×Z

Therefore moment of the entire area, above the fibre AA about the N.A = a

If and is integration

Moment of inertia of the section

Substituting in the expression for shear stress

Where b=width of the fibre AA =

Hence shear stress varies parabolically over the depth. Its value is zero at the extreme fibres where and its value is maximum when at the N.A and is given by

Thus in circular sections shear stress is maximum at the centre and is equal to 4/3 times the average stress

C) Triangular Section

Fig.6 Triangular Section

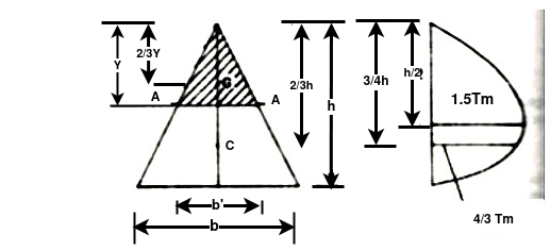
Let AA be a fibre distance y from the top.

Shear stress in general

i) at

ii) at

At the centroid substituting in (1)

Or substituting in the expression for ,

Thus maximum shear stress occurs at the half the depth and its value is 1.5 times the average shear stress in the case of an isosceles triangle.

Q5) Explain Determination of Bending Stresses.A5)

Determination of Bending Stresses –

The general formula for bending or normal stress on the section is given by:

= Where,

M = Internal bending moment about the section’s neutral axis

y = Perpendicular distance from the neutral axis to a point on the section

I = Moment of Inertia of the section area about the neutral axis

It is obvious to see that the bending stress will be maximised by the distance from the neutral axis (y). Thus, the maximum bending stress will occur either at the TOP or the BOTTOM of the beam section depending on which distance is larger.

Where,

c = Perpendicular distance from the neutral axis to the farthest point on the section

Q6) Explain Section Modulus in detail.A6)

Section Modulus –

To calculate the section modulus, the following formula applies:

Z =

Where,

I = moment of inertia,

y = distance from centroid to top or bottom edge of the rectangle

For symmetrical sections the value of Z is the same above or below the centroid.

For asymmetrical sections, two values are found: Z max and Z min.

Q7) Explain Design of Simple Beam Section in detail.A7)

Design of Simple Beam Section –

For a simple floor beam, I-sections are used.

M = σ

= Z (section modulus)

Therefore, M = z σ

When beams are loaded, bending stresses are developed at all sections.

The bending stresses developed in beams can be determined by the equation theory of simple bending.

For laterally supported beams, the permissible bending stress in tension as well as in compression should not exceed σbc or σbt = 0.66fy

For laterally unsupported beams, the permissible stress in bending compression is calculated by using tables from the IS code book (IS:800).

Load carrying capacity of the Beam

From structural steel tables for the given beam, the section modulus () is obtained.

Depending upon whether the beam is laterally restrained or unrestrained; the value of permissible stress in bending compression (σbc) is calculated.

The moment of resistance of the beam is found out.

MR = σ bc

Equating the moment of resistance to the maximum bending moment equation, the total load (w) the beam can carry is calculated.

Q9) Explain Derivation of Torsion equation and its Assumptions in detail.A9)

Derivation of Torsion equation and its Assumptions A) Torsion equation

Torsion equation or torsion constant is defined as the geometrical property of a bar’s cross-section that is involved in the axis of the bar that has a relationship between the angle of twist and applied torque.

The SI unit of Torsion equation is m4.

The torsion equation is given as follows:

Where,

T - torsional moment, N-mm

J - polar moment of inertia, mm4

 - shear stress in the element, N/mm2

r- distance of element from centre of shaft, mm

G - modulus of rigidity, N/mm2

- angle of twist, rad

L- length of shaft, mm

B) Derivation

Consider a solid circular shaft with radius R that is subjected to a torque T at one end and the other end under the same torque.

Angle in radius =

Arc AB = RӨ = Lγ

Where,

A and B: two fixed points on the circular shaft

γ: angle subtended by AB

(Modulus of rigidity)

Where,

𝞃: shear stress

γ: shear strain

Consider a small strip of radius with thickness dr that is subjected to shear stress.

Where,

r: radius of small strip

dr: thickness of the strip

γ: shear stress

(torque at the centre of the shaft)

(substituting for 𝛕’)

(after integrating and substituting for R)

Therefore, this equation is Torsion equation.

C) Assumptions

Following are the assumptions made for the derivation of torsion equation:

The material is homogeneous (elastic property throughout)
The material should follow Hook’s law
The material should have shear stress proportional to shear strain
The cross-sectional area should be plane
The circular section should be circular
Every diameter of the material should rotate through the same angle
The stress of the material should not exceed the elastic limit

Q9) Explain Torsional Rigidity in detail.A9)

Torsional Rigidity

From the torsion equation,

Angle of twist,

Where,

T - Torsional moment, N-mm

J - Polar moment of inertia, mm4

G - Modulus of rigidity, N/mm2 (sometimes denoted by C)

 - angle of twist, rad

For a given specimen, the shaft properties like length L, polar modulus J and material properties like rigidity modulus G are constants and hence the angle of twist is directly proportional to the twisting moment or torque producing the twist.

Torque producing twist in a shaft is similar to the bending moment producing bend or deflection in a beam. Similar to the flexural rigidity in beams expressed by EI, torsional rigidity is expressed as GJ which can be defined as the torque required to produce a twist of unit radian per unit length of the shaft.

Q10) Explain Principal Stress and Maximum Shear Stress in detail.A10)

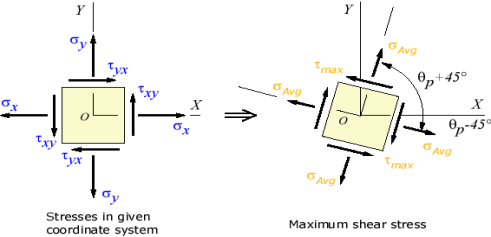
Principal Stress and Maximum Shear Stress

A) Principal Stress –

There exists an angle qp where the shear stress tx'y' becomes zero. That angle is found by setting tx'y' to zero in the above shear transformation equation and solving for q (set equal to qp). The result is,

The angle qp defines the principal directions where the only stresses are normal stresses. These stresses are called principal stresses and are found from the original stresses (expressed in the x, y, z directions) via,

The transformation to the principal directions can be illustrated as:

Fig 7. Principal Stress

B) Maximum Shear Stress –

Another important angle, s, is where the maximum shear stress occurs. This is found by finding the maximum of the shear stress transformation equation, and solving for . The result is,

The maximum shear stress is equal to one-half the difference between the two principal stresses,

= =

The transformation to the maximum shear stress direction can be illustrated as:

Fig 8. Maximum Shear Stress

Part C) Shear Stresses –

The bending stress is due to bending moment at the section.
The bending stress acting longitudinally and its intensity is directly proportional to its distance from neutral axis.
A typical beam section is subjected to shear force in addition to bending moment.
The variation of shearing stress, which is due to the presence of shear force is studied.

Sign Up