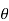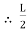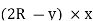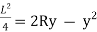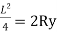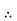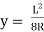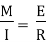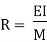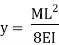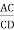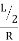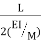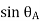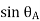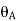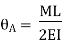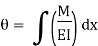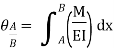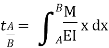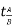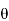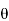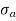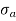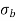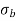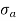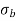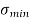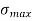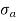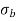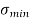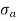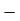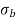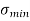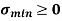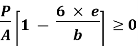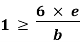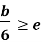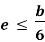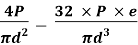Relationship between Moment, Slope and Deflection – Let, L = Span of Beam M = Bending Moment R = Radius of curvature of beam after bending Y = Deflection of beam at centre
Fig No 4.1
From the above figure, AC
In practice, deflection of beam y is very small and square of y is negligible.
By using Bending Formula,
Put the value of R in eq. no 1, we get
From the geometry of fig.
Since,
|
|
Theorem 1 – The change in slope between any two points on the elastic curve equals the area of the M/EI (moment) diagram between these two points.
Where, M = Moment EI = Flexural Rigidity
A, B = Points on Elastic curve
Theorem 2 – The vertical deviation of a point A on an elastic curve with respect to the tangent which is extended from another point B equals the moment of the area under the M/EI diagram between those two points (A and B). This moment is computed about point A where the deviation from B to A is to be determined.
Where, M = Moment EI = Flexural Rigidity
A, B = Points on Elastic curve
Rules of Sign Convention –
|
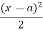 not
not  and integration of
and integration of 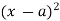 will be
will be 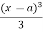 and so on.Step – IV: After first integration write the first integration constant (A) after first terms and after second time integration write the second integration constant (B) after A.x. Constant A and B are valid for all values of x.Step – V: Using Boundary condition find A and B at a point x = p if any term in Macaulay’s method, (x-a) is negative (-ve) the term will be neglected.Q5) Explain Buckling and Stability in detail.A5)Buckling and Stability –A) Buckling –
and so on.Step – IV: After first integration write the first integration constant (A) after first terms and after second time integration write the second integration constant (B) after A.x. Constant A and B are valid for all values of x.Step – V: Using Boundary condition find A and B at a point x = p if any term in Macaulay’s method, (x-a) is negative (-ve) the term will be neglected.Q5) Explain Buckling and Stability in detail.A5)Buckling and Stability –A) Buckling –Combined Bending and Direct Stress –
σ = σ = P/A + M/Z |
Fig No 4.2 Combined Bending and Direct Stress
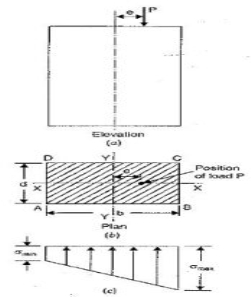
The stress distribution form face A to face B as shown in the figure.
Fig No 4.3 Stress Distribution
|
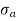 greater than
greater than 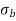 ), then the stress throughout the section will be compressive3.If direct stress is equal to bending stress (
), then the stress throughout the section will be compressive3.If direct stress is equal to bending stress (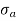 =
= 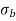 ), then the tensile stress will be zero.4.If direct stress is less than bending stress (
), then the tensile stress will be zero.4.If direct stress is less than bending stress ( less than
less than 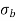 ), then there will be tensile stress.5.Hence for no tensile stress in the section, the direct stress will be greater than or equal to bending stress. Q6) Explain Middle Third Rule in detail.A6)
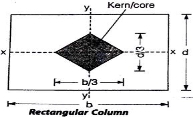
), then there will be tensile stress.5.Hence for no tensile stress in the section, the direct stress will be greater than or equal to bending stress. Q6) Explain Middle Third Rule in detail.A6)Middle Third Rule –
Fig No 4.4 Rectangular Column
|
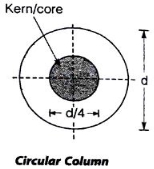
A7) Middle Quarter Rule –
Fig No 4.5 Circular Column
|
|
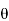 anticlockwise, the change of slope is positive, if
anticlockwise, the change of slope is positive, if 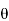 is clockwise.
is clockwise.