ISM
Unit - 5Helical and Leaf Spring Q1) Explain Helical Spring in detail.A1) Helical spring
The figures below show the schematic representation of a helical spring acted upon by a tensile load F (Fig.1(a)) and compressive load F (Fig.1(b)). The circles denote the cross section of the spring wire. The cut section, i.e. from the entire coil somewhere we make a cut, is indicated as a circle with shade. If we look at the free body diagram of the shaded region only (the cut section) then we shall see that at the cut section, vertical equilibrium of forces will give us force, F as indicated in the figure. This F is the shear force. The torque T, at the cut section and it’s direction is also marked in the figure. There is no horizontal force coming into the picture because externally there is no horizontal force present. So from the fundamental understanding of the free body diagram one can see that any section of the spring is experiencing a torque and a force. Shear force will always be associated with a bending moment. However, in an ideal situation, when force is acting at the Centre of the circular spring and the coils of spring are almost parallel to each other, no bending moment would result at any section of the spring (no moment arm), except torsion and shear force. The Fig.2 will explain the fact stated above.
Q2) Explain Leaf Spring in detail.A2) Leaf Spring A leaf spring is a simple form of spring commonly used for the suspension in wheeled vehicles. Originally called a laminated or carriage spring, and sometimes referred to as a semi-elliptical spring, elliptical spring, or cart spring. A leaf spring takes the form of a slender arc-shaped length of spring steel of rectangular cross-section. In the most common configuration, the centre of the arc provides location for the axle, while loops formed at either end provide for attaching to the vehicle chassis. For very heavy vehicles, a leaf spring can be made from several leaves stacked on top of each other in several layers, often with progressively shorter leaves. Leaf springs can serve locating and to some extent damping as well as springing functions. While the interleaf friction provides a damping action, it is not well controlled and results in station in the motion of the suspension. For this reason, some manufacturers have used mono-leaf springs. A leaf spring can either be attached directly to the frame at both ends or attached directly at one end, usually the front, with the other end attached through a shackle, a short swinging arm. The shackle takes up the tendency of the leaf spring to elongate when compressed and thus makes for softer springiness. Some springs terminated in a concave end, called a spoon end (seldom used now), to carry a swivelling member.
Q3) Explain Deflection of springs by energy method.A3) Deflection of springs by energy method
Q4) Explain Closed - coiled helical spring subjected to an axial load A4)Closed - coiled helical spring subjected to an axial load :
--Consider a small element mn n’m’ of the spring wire subtending an angle ∂θ at the center of the spring axis, say under the action of twisting moment T = WR (acting on every wire section along the coil) angular twist ∂θ as shown in fig 4 vertical deflection dδ = R δ θangular twist , δθ = 
because Rd∅ = d L = length of wire considered Cc’ dδ = R δθ = 
= 
T ,Twisting moment at any section is same i. e. , WR total axial deflection , δ = 0∫2nπ 
= 
* 2nm n= No. of turns of the spring Total angle subtended to coil at the axis of spring , ∅ = 2nπ polar moment of inertia of wire , J =πd4//32.So, Axial deflection δ = 
*2nπ = 
Q5) Explain Closed - coiled helical spring subjected to an axial momentA5)
Fig 5 shows a closed coiled Helical spring subjected to an axial couple M. the effect of the couple is to rotate end B of the spring with respect to end n.
Q6) Explain Open – coiled Helical Spring.A6) Open – coiled Helical Spring :-Say, an open-coiled Helical Spring of mean coil Radius R is subjected to an axial load W.WR = Total moment on spring wireWR cos α = T' = Twisting moment on a small element of length dl at the centers of coilWR sin α = M' = B.M. on small element of length dl in the place of coil.Due to twisting moment T' there will be angular twist δϕ' & due to B.M. M' , there will be an angular rotation δϕ' . δϕ' has two components δϕ' cos α & δϕ' sin α.δθ = Angular twist about XX axis = δϕ' cos α + δϕ' sin α.δϕ = angular rotation about Y Y axis = mm - qr= δϕ' sin α - δϕ' cos α.Moreover , δϕ' = 
& δϕ' = 
Total angular Twist θ, about XX-axis. θ = 0∫L δθ = 0∫L 
+
= 0∫L(
+ 
) δLAngular Twist θ = (
+ 
) LL = 2πnRsecα , put in above equation.Axial deflection , δ = Rθ .δ = 2πWR2secα (
+ 
)Total Angular rotation about Y Y-axis ϕ = 0∫L δθ = 0∫L (
+
) δL Q7) Explain Open – coiled Helical Spring subjected to axial moment.A7)
Q8) Explain Thin cylinders in detail.A8) Thin cylindersIf the wall thickness is less than about 7% of the inner diameter then the cylinder may be treated as a thin one. Thin walled cylinders are used as boiler shells, pressure tanks, pipes and in other low pressure processing equipment’s. In general three types of stresses are developed in pressure cylinders viz.circumferential or hoop stress, longitudinal stress in closed end cylinders and radial stresses. These stresses are demonstrated in figure-11
Fig.7 (a) Circumferential stress (b) Longitudinal stress and (c) Radial stress developed in thin cylinders.In a thin walled cylinder the circumferential stresses may be assumed to be constant over the wall thickness and stress in the radial direction may be neglected for the analysis. Considering the equilibrium of a cut out section the circumferential stress σθ and longitudinal stress σz can be found. Consider a section of thin cylinder of radius r, wall thickness t and length L and subjected to an internal pressure p as shown in figure-7(a). Q9) Explain Thick cylinders and sphere in detail.A9) Thick cylindrical shell
Q10) Explain Difference between thin walled and thick walled pressure vessels in detail.A10) Difference between thin walled and thick walled pressure vesselsThe distinction between thin vs. thick wall pressure vessels is determined by the ratio between the mean radius of the vessel and the thickness of the wall. If this ratio is greater than 10, the vessel is considered a thin wall pressure vessel. If the ratio is less than 10, the vessel is considered a thick wall pressure vessel. 
Means Thin wall P.V.In operation, in a thin wall pressure vessel, stresses developed in the (thin) wall can conservatively be assumed to be uniform. These are the stresses students are familiar calculating using ASME Section I PG-27 or Section VIII Div. I UG-27. In fact, most of the pressure vessels powers engineers will work with are of a thin-wall type. In contrast, a thick wall pressure vessel develops a greater (circumferential) stress on the inside surface of the vessel and it reduces towards the outside diameter. The design calculations for this type of vessels are only covered in the ASME Section VIII (Pressure Vessels) code, Mandatory Appendix 1 (Supplementary Design Formulas). The circumferential stress (or hoop stress) acting on a longitudinal cross-section is derived is 
Design problems most typically deal with finding the minimum required wall thickness, therefore the above formula is more useful expressed as: 
Longitudinal stress demonstrated and derived as 
Spherical pressure vessel stress is calculated in the same way as the longitudinal stress. You may conclude that a spherical pressure vessel will require a thinner shell, theoretically one half, than a cylindrical pressure vessel operating at the same pressure and temperature, and therefore it would be a preferred shape. Reality is that while most of that is true, it is difficult to manufacture a spherical shell.
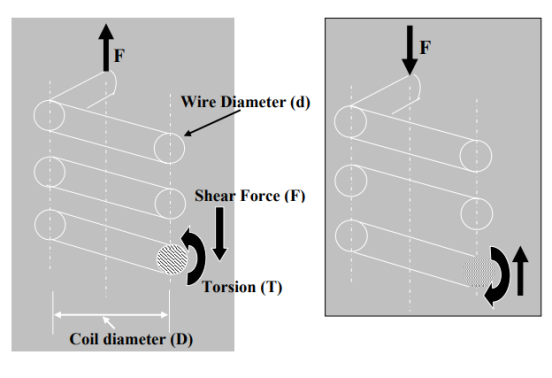
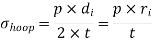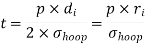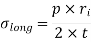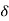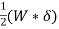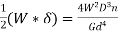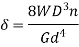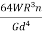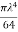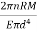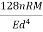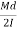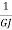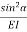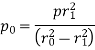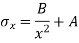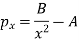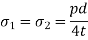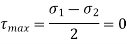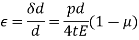Fig 1 (a) Fig 1 (b)
|
Fig.2 |
Fig.3
|
= |
Fig.4
|
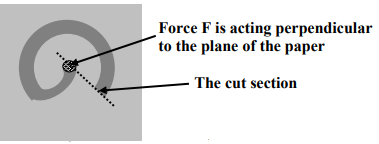
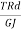because Rd∅ = d L = length of wire considered Cc’ dδ = R δθ = 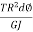= 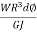T ,Twisting moment at any section is same i. e. , WR total axial deflection , δ = 0∫2nπ 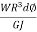= 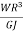* 2nm n= No. of turns of the spring Total angle subtended to coil at the axis of spring , ∅ = 2nπ polar moment of inertia of wire , J =πd4//32.So, Axial deflection δ = 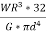*2nπ = 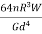Q5) Explain Closed - coiled helical spring subjected to an axial momentA5)
|
Fig.6 |
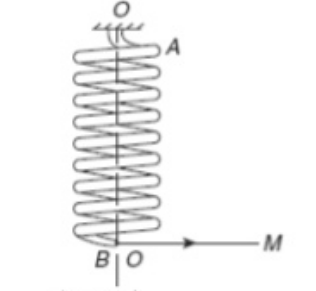
Helix angle X is very small. ϕ is the total angle through which one end of the spring is turned relative to the other , when couple M is applied. Work done on spring = (½) Mϕ .
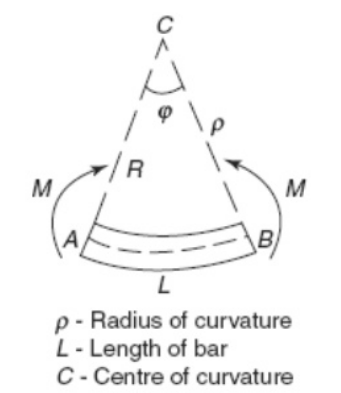
Fig 6 shows a b AB of Length subjected to Bending moment M rϕ = L ϕ = L/r , Where r = Radius of Curvature. From Flexure Formula
∴ ϕ = L = 2nπR , I =
∴ ϕ =
∴ δ = |
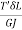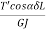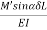& δϕ' = Total angular Twist θ, about XX-axis. θ = 0∫L δθ = 0∫L += 0∫L( 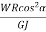+ 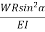) δLAngular Twist θ = ( 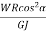+ 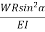) LL = 2πnRsecα , put in above equation.Axial deflection , δ = Rθ .δ = 2πWR2secα ( 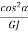+ )Total Angular rotation about Y Y-axis ϕ = 0∫L δθ = 0∫L (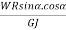+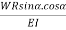) δL Q7) Explain Open – coiled Helical Spring subjected to axial moment.A7)Open coiled Helical Spring subjected to axial moment An open- coiled helical spring of mean coil radius R, Helix angle α & number of turns n is subjected to an axial moment m as shown in fig. Components of M are M' = M cos α = bending moment & T' = M sin α = Twisting moment δθ' = Angular Twist due to T' δθ' = δϕ = Angular rotation due to M' about y' y' axis = δθ = Angular Twist about xx-axis = δ ϕ ' sin α - δ ϕ ' cos α. Δθ = (
Total angular Twist . θ = ∫δθ = 0∫L M sin α cos α( L = 2 π n R sec α ∴ ϕ (Total Angular Rotation) = 2π n R sec α( |
|
1) The radial pressure ‘px’ (compressive) 2) The hoop stress fx (tensile) 3) The longitudinal tensile stress po(tensile)
Thin spherical shells
|
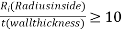Means Thin wall P.V.
0 matching results found