Module-3
Formal logic, group, ring, and field
Question-1: What are the basic logical operations?
Sol.
Basic logical operations-
1. Conjunction- p ⋀ q
Any two propositions can be combined by the word “and” to form a compound proposition called the conjunction of the original propositions. Symbolically,
P ∧ q
Read “p and q,” denotes the conjunction of p and q. Since p ∧q is a proposition it has a truth value and this truth
Value depends only on the truth values of p and q.
Note- If p and q are true, then p ∧q is true; otherwise p ∧q is false.
2. Disjunction, p ∨q
Any two propositions can be combined by the word “or” to form a compound proposition called the disjunction of the original propositions. Symbolically,
p∨q
Read “p or q,” denotes the disjunction of p and q. The truth value of p ∨q depends only on the truth values of p
And q as follows-
If p and q are false, then p ∨q is false; otherwise, p ∨q is true
Negation-
Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p,” is denoted by
¬p
The truth value of ¬p depends on the truth value of p as follows-
If p is true, then ¬p is false; and if p is false, then ¬p is true
Question-2: construct the truth table for p ∨  q.
q.
Sol.
p | Q | 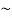 | p ∨ 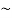 |
T | T | F | T |
T | F | T | T |
F | T | F | F |
F | F | T | T |
Question-3: Define tautology and contradiction.
Sol.
A statement formula that is true for all possible values of its propositional variables is called a Tautology.
Ex.-  is a tautology
is a tautology
Contradiction-
Similarly, a proposition that is false for all possible truth values of the simple propositions that constitute it is called a contradiction.
Question-4: Show that p ∨~p is a tautology.
Sol. First we will construct the truth table for (p ∨~p)
p | 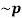 | (p ∨~p) |
T | F | T |
T | T | T |
p∨~p is always true.
Hence p ∨~p is a tautology.
Question-5: Show that
((p ∨~q) ∧(~p ∨~q)) ∨q is a tautology.
Sol. Consider
((p ∨~q) ∧(~p ∨~q)) ∨q
≡((p ∨~q) ∧~p ∨(p ∨~q) ∧~q) ∨q
≡((p ∧~p) ∨(~q ∧~p) ∨(p ∧~q) ∨(~q ∧~q)) ∨q
≡(f ∨(~q ∧~p) ∨(p ∧~q) ∨~q) ∨q
≡(~ q ∧~p) ∨(p ∧~q) ∨~q ∨q
≡(~ q ∧~p) ∨(p ∧~q) ∨t(Since ~q ∨q ≡t)
≡ t
Hence ((p ∨~q) ∧(~p ∨~q)) ∨q is a tautology.
Question-6: Obtain disjunctive normal form ofp ∨(~p →(q ∨(q →~r)))
Sol. p ∨(~p →(q ∨(q →~r)))
≡p ∨(~p →q ∨(~q ∨~r)))
≡p∨(p ∨(q ∨(~q ∨~r)))
≡p∨p ∨q ∨~q ∨~r
≡p∨q ∨~q ∨~r
Therefore, the disjunctive normal form of
p∨(~p →(q ∨( ~q →~r))) is p ∨q ∨~q ~r
Question-7: Obtain the principal disjunctive normal form of (~ p ∨~ q)→ (~ p ∧r ).
Sol. (~ p ∨~ q)→ (~ p ∧r )
⇔~(~ p ∨~ q) ∨ (~ p ∧r )
⇔~ (~(p ∧q)) ∨ (~ p ∧r )
⇔( p∧q) ∨ (~ p ∧r )
⇔( p∧q ∧ (r ∨~ r )) ∨ (~ p ∧r ∧ (q ∨~ q))
⇔( p∧q ∧r) ∨ ( p ∧q ∧~ r) ∨ (~ p ∧r ∧q) ∨ (~ p ∧r ∧~ q)
The principal disjunctive normal form of the given formula is
( p∧q ∧r) ∨( p∧q ∧~ r) ∨ (~ p ∧q ∧r) ∨ (~ p ∧~ q ∧r)
Question-8: Obtain the principal disjunctive normal form of ~p ∨q.
Sol. ~p ∨q ≡(~p ∧(q ∨~q)) ∨(q ∧(p ∨~p))
≡(~p ∧q) ∨(~p ∧~q) ∨(q ∧p) ∨(q ∧~p)
≡(~p ∧q) ∨(~p ∧~q) ∨(p ∧q)
Therefore (~p ∧q) ∧(~p ∧~q) ∧(p ∧q) is the required principal disjunctive normal form.
Question-9: Define the semigroup and monoid.
Sol.
Semi-group-
Suppose * is the binary operation on S, where S is a non-empty set then the algebraic (S, *) is said to be a semigroup if the operation * is associative.
A semigroup has-
- A binary operation * defined on the elements of S.
- Closure, a * b whenever a, b
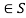 .
. - Associativity (a*b)*c = a*(b*c) for all a, b, c
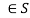
Monoids-
An algebraic system (M, *) is said to be monoid if-
- (a*b)*c = a*(b*c) for every for all a, b, c
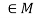 .
. - There exists an element e
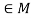 such that e*a = a*e = a for every for all a
such that e*a = a*e = a for every for all a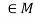
Question-10: If G = {1, -1, i, -i} where i= 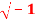 , then show that G is an abelian group with respect to multiplication as a binary operation.
, then show that G is an abelian group with respect to multiplication as a binary operation.
Sol.
First, we will construct a composition table-
. | 1 | -1 | I | -i |
1 | 1 | -1 | I | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | i | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties holds.
∴Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied
Hence (G, ⋅) is an abelian group.
Question-11: let S = {a, b, c} and f = 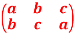
Sol.
Here we can write-
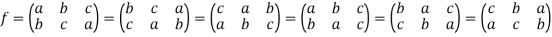
So that there are 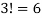 ways to write f.
ways to write f.
Question-12: Define the ring and field.
Sol.
Definition-
An algebraic system (R, +, .) is called a ring if the binary operations ‘+’ and ‘. ’ R satisfy the following conditions-
1. (R, +) is an abelian group
2. (R, .) is a semi-group.
3. The operation ‘ .’ is distributive over +, that is for any, a, b, c belongs to R.
a .(b + c) = a . b + a . c
And
(b + c) . a = b. a + c. a
Field-
“A commutative division ring is called a field.”
Note-
1. A finite integral domain is a field.
2. The characteristic of the ring of integers (Z, +, .) is zero
3. The characteristic of an integral domain is either a prime or zero.
4. The characteristic of a field is either a prime or zero.
Module-3
Formal logic, group, ring, and field
Question-1: What are the basic logical operations?
Sol.
Basic logical operations-
1. Conjunction- p ⋀ q
Any two propositions can be combined by the word “and” to form a compound proposition called the conjunction of the original propositions. Symbolically,
P ∧ q
Read “p and q,” denotes the conjunction of p and q. Since p ∧q is a proposition it has a truth value and this truth
Value depends only on the truth values of p and q.
Note- If p and q are true, then p ∧q is true; otherwise p ∧q is false.
2. Disjunction, p ∨q
Any two propositions can be combined by the word “or” to form a compound proposition called the disjunction of the original propositions. Symbolically,
p∨q
Read “p or q,” denotes the disjunction of p and q. The truth value of p ∨q depends only on the truth values of p
And q as follows-
If p and q are false, then p ∨q is false; otherwise, p ∨q is true
Negation-
Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p,” is denoted by
¬p
The truth value of ¬p depends on the truth value of p as follows-
If p is true, then ¬p is false; and if p is false, then ¬p is true
Question-2: construct the truth table for p ∨  q.
q.
Sol.
p | Q | 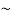 | p ∨ 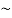 |
T | T | F | T |
T | F | T | T |
F | T | F | F |
F | F | T | T |
Question-3: Define tautology and contradiction.
Sol.
A statement formula that is true for all possible values of its propositional variables is called a Tautology.
Ex.- 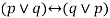 is a tautology
is a tautology
Contradiction-
Similarly, a proposition that is false for all possible truth values of the simple propositions that constitute it is called a contradiction.
Question-4: Show that p ∨~p is a tautology.
Sol. First we will construct the truth table for (p ∨~p)
p |  | (p ∨~p) |
T | F | T |
T | T | T |
p∨~p is always true.
Hence p ∨~p is a tautology.
Question-5: Show that
((p ∨~q) ∧(~p ∨~q)) ∨q is a tautology.
Sol. Consider
((p ∨~q) ∧(~p ∨~q)) ∨q
≡((p ∨~q) ∧~p ∨(p ∨~q) ∧~q) ∨q
≡((p ∧~p) ∨(~q ∧~p) ∨(p ∧~q) ∨(~q ∧~q)) ∨q
≡(f ∨(~q ∧~p) ∨(p ∧~q) ∨~q) ∨q
≡(~ q ∧~p) ∨(p ∧~q) ∨~q ∨q
≡(~ q ∧~p) ∨(p ∧~q) ∨t(Since ~q ∨q ≡t)
≡ t
Hence ((p ∨~q) ∧(~p ∨~q)) ∨q is a tautology.
Question-6: Obtain disjunctive normal form ofp ∨(~p →(q ∨(q →~r)))
Sol. p ∨(~p →(q ∨(q →~r)))
≡p ∨(~p →q ∨(~q ∨~r)))
≡p∨(p ∨(q ∨(~q ∨~r)))
≡p∨p ∨q ∨~q ∨~r
≡p∨q ∨~q ∨~r
Therefore, the disjunctive normal form of
p∨(~p →(q ∨( ~q →~r))) is p ∨q ∨~q ~r
Question-7: Obtain the principal disjunctive normal form of (~ p ∨~ q)→ (~ p ∧r ).
Sol. (~ p ∨~ q)→ (~ p ∧r )
⇔~(~ p ∨~ q) ∨ (~ p ∧r )
⇔~ (~(p ∧q)) ∨ (~ p ∧r )
⇔( p∧q) ∨ (~ p ∧r )
⇔( p∧q ∧ (r ∨~ r )) ∨ (~ p ∧r ∧ (q ∨~ q))
⇔( p∧q ∧r) ∨ ( p ∧q ∧~ r) ∨ (~ p ∧r ∧q) ∨ (~ p ∧r ∧~ q)
The principal disjunctive normal form of the given formula is
( p∧q ∧r) ∨( p∧q ∧~ r) ∨ (~ p ∧q ∧r) ∨ (~ p ∧~ q ∧r)
Question-8: Obtain the principal disjunctive normal form of ~p ∨q.
Sol. ~p ∨q ≡(~p ∧(q ∨~q)) ∨(q ∧(p ∨~p))
≡(~p ∧q) ∨(~p ∧~q) ∨(q ∧p) ∨(q ∧~p)
≡(~p ∧q) ∨(~p ∧~q) ∨(p ∧q)
Therefore (~p ∧q) ∧(~p ∧~q) ∧(p ∧q) is the required principal disjunctive normal form.
Question-9: Define the semigroup and monoid.
Sol.
Semi-group-
Suppose * is the binary operation on S, where S is a non-empty set then the algebraic (S, *) is said to be a semigroup if the operation * is associative.
A semigroup has-
- A binary operation * defined on the elements of S.
- Closure, a * b whenever a, b
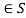 .
. - Associativity (a*b)*c = a*(b*c) for all a, b, c
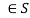
Monoids-
An algebraic system (M, *) is said to be monoid if-
- (a*b)*c = a*(b*c) for every for all a, b, c
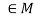 .
. - There exists an element e
 such that e*a = a*e = a for every for all a
such that e*a = a*e = a for every for all a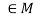
Question-10: If G = {1, -1, i, -i} where i= 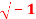 , then show that G is an abelian group with respect to multiplication as a binary operation.
, then show that G is an abelian group with respect to multiplication as a binary operation.
Sol.
First, we will construct a composition table-
. | 1 | -1 | I | -i |
1 | 1 | -1 | I | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | i | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties holds.
∴Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied
Hence (G, ⋅) is an abelian group.
Question-11: let S = {a, b, c} and f = 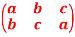
Sol.
Here we can write-
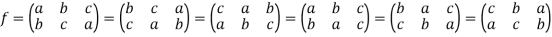
So that there are  ways to write f.
ways to write f.
Question-12: Define the ring and field.
Sol.
Definition-
An algebraic system (R, +, .) is called a ring if the binary operations ‘+’ and ‘. ’ R satisfy the following conditions-
1. (R, +) is an abelian group
2. (R, .) is a semi-group.
3. The operation ‘ .’ is distributive over +, that is for any, a, b, c belongs to R.
a .(b + c) = a . b + a . c
And
(b + c) . a = b. a + c. a
Field-
“A commutative division ring is called a field.”
Note-
1. A finite integral domain is a field.
2. The characteristic of the ring of integers (Z, +, .) is zero
3. The characteristic of an integral domain is either a prime or zero.
4. The characteristic of a field is either a prime or zero.
Module-3
Formal logic, group, ring, and field
Question-1: What are the basic logical operations?
Sol.
Basic logical operations-
1. Conjunction- p ⋀ q
Any two propositions can be combined by the word “and” to form a compound proposition called the conjunction of the original propositions. Symbolically,
P ∧ q
Read “p and q,” denotes the conjunction of p and q. Since p ∧q is a proposition it has a truth value and this truth
Value depends only on the truth values of p and q.
Note- If p and q are true, then p ∧q is true; otherwise p ∧q is false.
2. Disjunction, p ∨q
Any two propositions can be combined by the word “or” to form a compound proposition called the disjunction of the original propositions. Symbolically,
p∨q
Read “p or q,” denotes the disjunction of p and q. The truth value of p ∨q depends only on the truth values of p
And q as follows-
If p and q are false, then p ∨q is false; otherwise, p ∨q is true
Negation-
Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p,” is denoted by
¬p
The truth value of ¬p depends on the truth value of p as follows-
If p is true, then ¬p is false; and if p is false, then ¬p is true
Question-2: construct the truth table for p ∨  q.
q.
Sol.
p | Q | 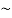 | p ∨ 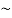 |
T | T | F | T |
T | F | T | T |
F | T | F | F |
F | F | T | T |
Question-3: Define tautology and contradiction.
Sol.
A statement formula that is true for all possible values of its propositional variables is called a Tautology.
Ex.- 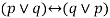 is a tautology
is a tautology
Contradiction-
Similarly, a proposition that is false for all possible truth values of the simple propositions that constitute it is called a contradiction.
Question-4: Show that p ∨~p is a tautology.
Sol. First we will construct the truth table for (p ∨~p)
p | 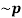 | (p ∨~p) |
T | F | T |
T | T | T |
p∨~p is always true.
Hence p ∨~p is a tautology.
Question-5: Show that
((p ∨~q) ∧(~p ∨~q)) ∨q is a tautology.
Sol. Consider
((p ∨~q) ∧(~p ∨~q)) ∨q
≡((p ∨~q) ∧~p ∨(p ∨~q) ∧~q) ∨q
≡((p ∧~p) ∨(~q ∧~p) ∨(p ∧~q) ∨(~q ∧~q)) ∨q
≡(f ∨(~q ∧~p) ∨(p ∧~q) ∨~q) ∨q
≡(~ q ∧~p) ∨(p ∧~q) ∨~q ∨q
≡(~ q ∧~p) ∨(p ∧~q) ∨t(Since ~q ∨q ≡t)
≡ t
Hence ((p ∨~q) ∧(~p ∨~q)) ∨q is a tautology.
Question-6: Obtain disjunctive normal form ofp ∨(~p →(q ∨(q →~r)))
Sol. p ∨(~p →(q ∨(q →~r)))
≡p ∨(~p →q ∨(~q ∨~r)))
≡p∨(p ∨(q ∨(~q ∨~r)))
≡p∨p ∨q ∨~q ∨~r
≡p∨q ∨~q ∨~r
Therefore, the disjunctive normal form of
p∨(~p →(q ∨( ~q →~r))) is p ∨q ∨~q ~r
Question-7: Obtain the principal disjunctive normal form of (~ p ∨~ q)→ (~ p ∧r ).
Sol. (~ p ∨~ q)→ (~ p ∧r )
⇔~(~ p ∨~ q) ∨ (~ p ∧r )
⇔~ (~(p ∧q)) ∨ (~ p ∧r )
⇔( p∧q) ∨ (~ p ∧r )
⇔( p∧q ∧ (r ∨~ r )) ∨ (~ p ∧r ∧ (q ∨~ q))
⇔( p∧q ∧r) ∨ ( p ∧q ∧~ r) ∨ (~ p ∧r ∧q) ∨ (~ p ∧r ∧~ q)
The principal disjunctive normal form of the given formula is
( p∧q ∧r) ∨( p∧q ∧~ r) ∨ (~ p ∧q ∧r) ∨ (~ p ∧~ q ∧r)
Question-8: Obtain the principal disjunctive normal form of ~p ∨q.
Sol. ~p ∨q ≡(~p ∧(q ∨~q)) ∨(q ∧(p ∨~p))
≡(~p ∧q) ∨(~p ∧~q) ∨(q ∧p) ∨(q ∧~p)
≡(~p ∧q) ∨(~p ∧~q) ∨(p ∧q)
Therefore (~p ∧q) ∧(~p ∧~q) ∧(p ∧q) is the required principal disjunctive normal form.
Question-9: Define the semigroup and monoid.
Sol.
Semi-group-
Suppose * is the binary operation on S, where S is a non-empty set then the algebraic (S, *) is said to be a semigroup if the operation * is associative.
A semigroup has-
- A binary operation * defined on the elements of S.
- Closure, a * b whenever a, b
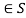 .
. - Associativity (a*b)*c = a*(b*c) for all a, b, c

Monoids-
An algebraic system (M, *) is said to be monoid if-
- (a*b)*c = a*(b*c) for every for all a, b, c
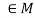 .
. - There exists an element e
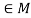 such that e*a = a*e = a for every for all a
such that e*a = a*e = a for every for all a
Question-10: If G = {1, -1, i, -i} where i= 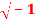 , then show that G is an abelian group with respect to multiplication as a binary operation.
, then show that G is an abelian group with respect to multiplication as a binary operation.
Sol.
First, we will construct a composition table-
. | 1 | -1 | I | -i |
1 | 1 | -1 | I | -i |
-1 | -1 | 1 | -i | i |
i | i | -i | -1 | 1 |
-i | -i | i | 1 | -1 |
It is clear from the above table that algebraic structure (G, .) is closed and satisfies the following conditions.
Associativity- For any three elements a, b, c ∈G (a ⋅b) ⋅c = a ⋅(b ⋅c)
Since
1 ⋅(−1 ⋅i) = 1 ⋅−i= −i
(1 ⋅−1) ⋅i= −1 ⋅i= −i
⇒1 ⋅(−1 ⋅i) = (1 ⋅−1) i
Similarly with any other three elements of G the properties holds.
∴Associative law holds in (G, ⋅)
Existence of identity: 1 is the identity element (G, ⋅) such that 1 ⋅a = a = a ⋅1 ∀a ∈G
Existence of inverse: 1 ⋅1 = 1 = 1 ⋅1 ⇒1 is inverse of 1
(−1) ⋅(−1) = 1 = (−1) ⋅(−1) ⇒–1 is the inverse of (–1)
i⋅(−i) = 1 = −i⋅i⇒–iis the inverse of iin G.
−i⋅i= 1 = i⋅(−i) ⇒iis the inverse of –iin G.
Hence inverse of every element in G exists.
Thus all the axioms of a group are satisfied.
Commutativity: a ⋅b = b ⋅a ∀a, b ∈G hold in G
1 ⋅1 = 1 = 1 ⋅1, −1 ⋅1 = −1 = 1 ⋅−1
i⋅1 = i= 1 ⋅i; i⋅−i= −i⋅i= 1 = 1 etc.
Commutative law is satisfied
Hence (G, ⋅) is an abelian group.
Question-11: let S = {a, b, c} and f = 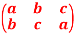
Sol.
Here we can write-
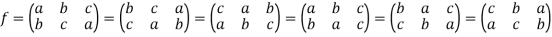
So that there are 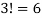 ways to write f.
ways to write f.
Question-12: Define the ring and field.
Sol.
Definition-
An algebraic system (R, +, .) is called a ring if the binary operations ‘+’ and ‘. ’ R satisfy the following conditions-
1. (R, +) is an abelian group
2. (R, .) is a semi-group.
3. The operation ‘ .’ is distributive over +, that is for any, a, b, c belongs to R.
a .(b + c) = a . b + a . c
And
(b + c) . a = b. a + c. a
Field-
“A commutative division ring is called a field.”
Note-
1. A finite integral domain is a field.
2. The characteristic of the ring of integers (Z, +, .) is zero
3. The characteristic of an integral domain is either a prime or zero.
4. The characteristic of a field is either a prime or zero.