Module-5
Lattices and Boolean Algebra
Questin-1: Find the number of ways to partition 10 peoples into four groups 
So that two teams contain 3 persons and two teams containing 2 persons.
Sol.
By using the above theorem, we get-
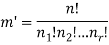
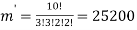 ordered partitions
ordered partitions
Here the group forms an unordered partition so that we divide m’ by 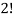 Because of the two cells with three elements each and
Because of the two cells with three elements each and 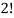 Because of the two cells with two elements each.
Because of the two cells with two elements each.
So that-
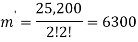
Question-2: There are 12 employees in a company. Find the number of ways that the 12 employees do three different tasks if four employees are to take each task.
Sol.
Here we find the number of ordered partitions of twelve employees into cells containing 4 employees each.
There are total - 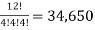 partitions
partitions
Hence the required number of ways, the employees can do the task is 34,650.
Question-3: What are sublattices and direct product.
Sol. Sub Lattices-
Let (L, ≤) be a lattice. A non-empty subset A of L is called a sublattice of L if
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
If A is a sublattice of L, then A is closed under the operations of ‘’ ⋅and ‘+’.
Direct product-
Let (L1, *, +) and (L2,∧, ∨) be two lattices. The algebraic system (L1 × L2,...,+)
In which the binary operation + and ‘’ ⋅are on L1 × L2 defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 )
For all (a1, b1) and (a2, b2) (a2 ,b2 ) ∈L1 × L2
Is called the direct product of the lattices L1 and L2.
Question-4: Let 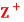 be the set of all positive integers and let D denote the relation “division” in
be the set of all positive integers and let D denote the relation “division” in 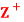 such that for any a, b ∈
such that for any a, b ∈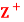 , a D b if a divides 6. Then (
, a D b if a divides 6. Then (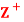 , D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
, D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
Sol.
The direct product of the lattices-
Let (L1, *, +) and 2 (L, ∧, ∨) be two lattices. The algebraic system (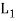 ×
× 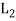 , ..., +) in which the binary operation + and ‘.’are on
, ..., +) in which the binary operation + and ‘.’are on 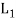 ×
× 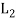 defined as
defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 ) for all (a1, b1) and (a2, b2) (a2 , b2 ) ∈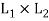 is called the direct product of the lattices
is called the direct product of the lattices 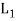 and
and 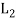
Question-5: Show that-
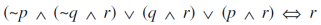
Sol.
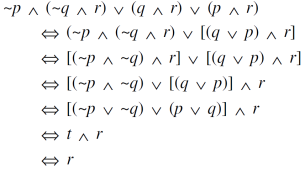
Note- ‘t’ denotes tautology
Question-6: Simplify z (y+z) ((x + y + z).
Sol.
z(y + z) (x + y + z)
= (z y + z z) (x + y + z)
= (z y + z) (x + y + z)
= z (y + 1) (x + y + z)
= z (x + y + z)
= z x + z y + z z
= z x + z y + z
= z (x + y + 1)
= z (x + 1)
= z
Question-7: Minimize the expression  +
+ + A B
+ A B
Sol.
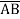 +
+ 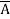 + A B
+ A B
= 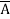 +
+ 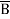 +
+ 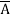 + A B
+ A B
= 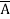 +
+ 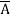 +
+ 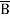 + A B
+ A B
= 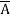 +
+ 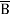 + A B
+ A B
= 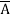 + A B +
+ A B + 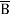
Hence
Question-8: What are OR gate and NOT gate.
Sol.
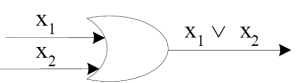
OR-gate-
This is a logic circuit with two or more than two inputs and outputs.
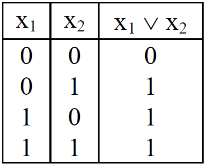
An OR-gate receive inputs  and gives the output, denoted by
and gives the output, denoted by  .
.
We use the standard pictorial representation of OR-gate as-
AND-gate-
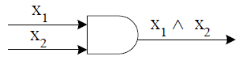
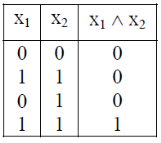
An AND-gate is a logic circuit having two or more than two inputs and one output.
The truth table and pictorial representation is given below-
Question-9: Express-
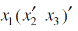
In an equivalent sum-of-products canonical form in three variables 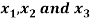
Sol.
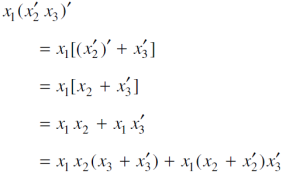
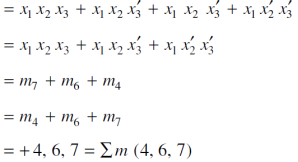
Question-10: What are the Kanaugh map.
Sol.
The Karnaugh method is a systematic method for simplifying Boolean function.
It is a graphical representation of the truth table with a square representing each minterm.
If a function has ‘n’ variables then the Karnaugh map will have 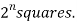
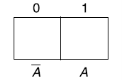
One variable Karnaugh map is-
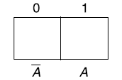
Two variable Kanaugh map representing minterm-
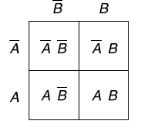
Or
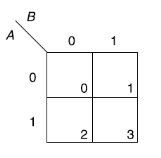
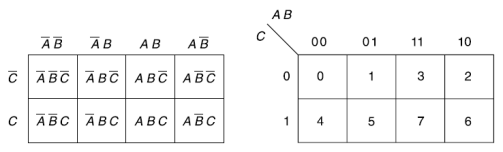
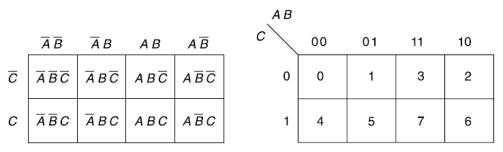
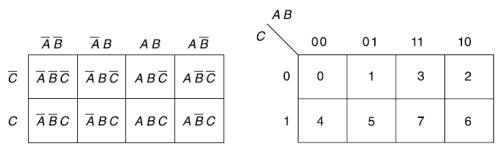
Karnaugh map for three variables-
Module-5
Module-5
Lattices and Boolean Algebra
Questin-1: Find the number of ways to partition 10 peoples into four groups 
So that two teams contain 3 persons and two teams containing 2 persons.
Sol.
By using the above theorem, we get-
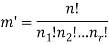
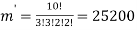 ordered partitions
ordered partitions
Here the group forms an unordered partition so that we divide m’ by 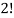 Because of the two cells with three elements each and
Because of the two cells with three elements each and 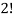 Because of the two cells with two elements each.
Because of the two cells with two elements each.
So that-
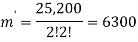
Question-2: There are 12 employees in a company. Find the number of ways that the 12 employees do three different tasks if four employees are to take each task.
Sol.
Here we find the number of ordered partitions of twelve employees into cells containing 4 employees each.
There are total - 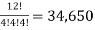 partitions
partitions
Hence the required number of ways, the employees can do the task is 34,650.
Question-3: What are sublattices and direct product.
Sol. Sub Lattices-
Let (L, ≤) be a lattice. A non-empty subset A of L is called a sublattice of L if
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
If A is a sublattice of L, then A is closed under the operations of ‘’ ⋅and ‘+’.
Direct product-
Let (L1, *, +) and (L2,∧, ∨) be two lattices. The algebraic system (L1 × L2,...,+)
In which the binary operation + and ‘’ ⋅are on L1 × L2 defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 )
For all (a1, b1) and (a2, b2) (a2 ,b2 ) ∈L1 × L2
Is called the direct product of the lattices L1 and L2.
Question-4: Let 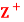 be the set of all positive integers and let D denote the relation “division” in
be the set of all positive integers and let D denote the relation “division” in 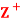 such that for any a, b ∈
such that for any a, b ∈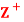 , a D b if a divides 6. Then (
, a D b if a divides 6. Then (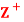 , D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
, D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
Sol.
The direct product of the lattices-
Let (L1, *, +) and 2 (L, ∧, ∨) be two lattices. The algebraic system (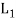 ×
× 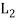 , ..., +) in which the binary operation + and ‘.’are on
, ..., +) in which the binary operation + and ‘.’are on 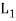 ×
× 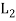 defined as
defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 ) for all (a1, b1) and (a2, b2) (a2 , b2 ) ∈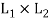 is called the direct product of the lattices
is called the direct product of the lattices 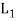 and
and 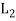
Question-5: Show that-
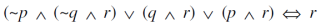
Sol.
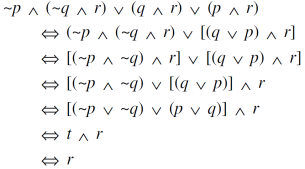
Note- ‘t’ denotes tautology
Question-6: Simplify z (y+z) ((x + y + z).
Sol.
z(y + z) (x + y + z)
= (z y + z z) (x + y + z)
= (z y + z) (x + y + z)
= z (y + 1) (x + y + z)
= z (x + y + z)
= z x + z y + z z
= z x + z y + z
= z (x + y + 1)
= z (x + 1)
= z
Question-7: Minimize the expression  +
+ + A B
+ A B
Sol.
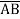 +
+ 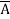 + A B
+ A B
= 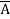 +
+ 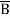 +
+ 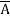 + A B
+ A B
= 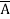 +
+ 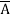 +
+ 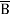 + A B
+ A B
= 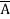 +
+ 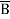 + A B
+ A B
= 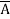 + A B +
+ A B + 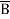
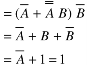
Hence
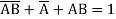
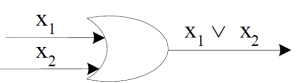
Question-8: What are OR gate and NOT gate.
Sol.
OR-gate-
This is a logic circuit with two or more than two inputs and outputs.
An OR-gate receive inputs 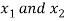 and gives the output, denoted by
and gives the output, denoted by 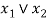 .
.
We use the standard pictorial representation of OR-gate as-
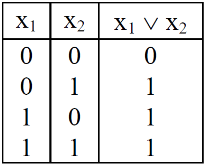
AND-gate-
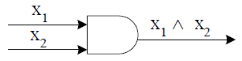
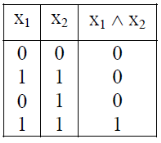
An AND-gate is a logic circuit having two or more than two inputs and one output.
The truth table and pictorial representation is given below-
Question-9: Express-
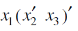
In an equivalent sum-of-products canonical form in three variables 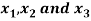
Sol.
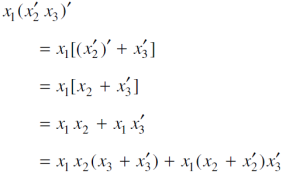
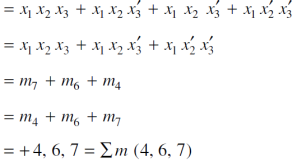
Question-10: What are the Kanaugh map.
Sol.
The Karnaugh method is a systematic method for simplifying Boolean function.
It is a graphical representation of the truth table with a square representing each minterm.
If a function has ‘n’ variables then the Karnaugh map will have 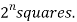
One variable Karnaugh map is-
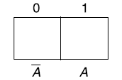
Two variable Kanaugh map representing minterm-
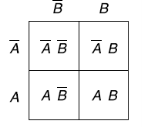
Or
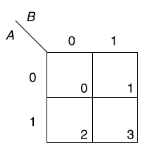
Karnaugh map for three variables-
Module-5
Lattices and Boolean Algebra
Questin-1: Find the number of ways to partition 10 peoples into four groups 
So that two teams contain 3 persons and two teams containing 2 persons.
Sol.
By using the above theorem, we get-
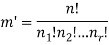
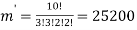 ordered partitions
ordered partitions
Here the group forms an unordered partition so that we divide m’ by 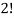 Because of the two cells with three elements each and
Because of the two cells with three elements each and 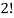 Because of the two cells with two elements each.
Because of the two cells with two elements each.
So that-
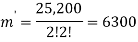
Question-2: There are 12 employees in a company. Find the number of ways that the 12 employees do three different tasks if four employees are to take each task.
Sol.
Here we find the number of ordered partitions of twelve employees into cells containing 4 employees each.
There are total - 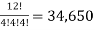 partitions
partitions
Hence the required number of ways, the employees can do the task is 34,650.
Question-3: What are sublattices and direct product.
Sol. Sub Lattices-
Let (L, ≤) be a lattice. A non-empty subset A of L is called a sublattice of L if
a + b ∈A and a ⋅b ∈A whenever a ∈A and b ∈A.
If A is a sublattice of L, then A is closed under the operations of ‘’ ⋅and ‘+’.
Direct product-
Let (L1, *, +) and (L2,∧, ∨) be two lattices. The algebraic system (L1 × L2,...,+)
In which the binary operation + and ‘’ ⋅are on L1 × L2 defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 )
For all (a1, b1) and (a2, b2) (a2 ,b2 ) ∈L1 × L2
Is called the direct product of the lattices L1 and L2.
Question-4: Let 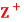 be the set of all positive integers and let D denote the relation “division” in
be the set of all positive integers and let D denote the relation “division” in 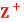 such that for any a, b ∈
such that for any a, b ∈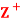 , a D b if a divides 6. Then (
, a D b if a divides 6. Then (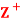 , D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
, D) is a lattice in which a + b = LCM of a and b and a ⋅b = GCD of a and b.
Sol.
The direct product of the lattices-
Let (L1, *, +) and 2 (L, ∧, ∨) be two lattices. The algebraic system (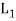 ×
× 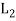 , ..., +) in which the binary operation + and ‘.’are on
, ..., +) in which the binary operation + and ‘.’are on 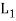 ×
× 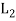 defined as
defined as
(a1, b1) ⋅(a2 ,b2 ) = (a1 ∗a2 , b1 ∧b2 )
(a1, b1 )+ (a2 ,b2 ) = (a1 ⊕a2 , b1 ∨b2 ) for all (a1, b1) and (a2, b2) (a2 , b2 ) ∈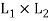 is called the direct product of the lattices
is called the direct product of the lattices 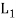 and
and 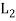
Question-5: Show that-
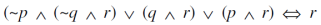
Sol.
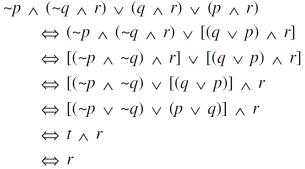
Note- ‘t’ denotes tautology
Question-6: Simplify z (y+z) ((x + y + z).
Sol.
z(y + z) (x + y + z)
= (z y + z z) (x + y + z)
= (z y + z) (x + y + z)
= z (y + 1) (x + y + z)
= z (x + y + z)
= z x + z y + z z
= z x + z y + z
= z (x + y + 1)
= z (x + 1)
= z
Question-7: Minimize the expression  +
+ + A B
+ A B
Sol.
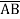 +
+ 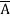 + A B
+ A B
= 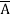 +
+ 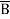 +
+ 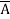 + A B
+ A B
= 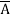 +
+ 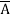 +
+ 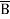 + A B
+ A B
= 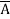 +
+ 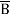 + A B
+ A B
= 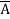 + A B +
+ A B + 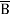
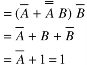
Hence
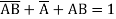
Question-8: What are OR gate and NOT gate.
Sol.
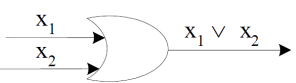
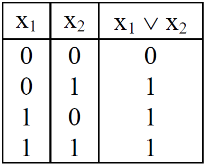
OR-gate-
This is a logic circuit with two or more than two inputs and outputs.
An OR-gate receive inputs 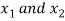 and gives the output, denoted by
and gives the output, denoted by 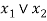 .
.
We use the standard pictorial representation of OR-gate as-
AND-gate-
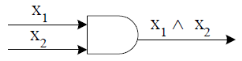
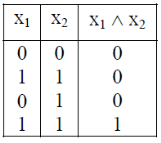
An AND-gate is a logic circuit having two or more than two inputs and one output.
The truth table and pictorial representation is given below-
Question-9: Express-
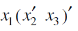
In an equivalent sum-of-products canonical form in three variables 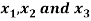
Sol.
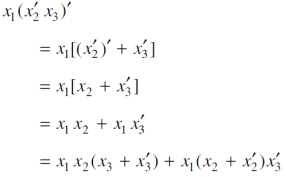
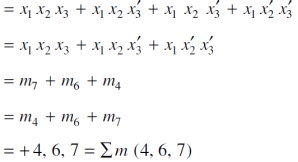
Question-10: What are the Kanaugh map.
Sol.
The Karnaugh method is a systematic method for simplifying Boolean function.
It is a graphical representation of the truth table with a square representing each minterm.
If a function has ‘n’ variables then the Karnaugh map will have 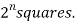
One variable Karnaugh map is-
Two variable Kanaugh map representing minterm-
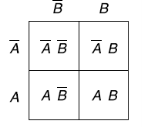
Or
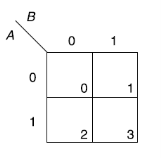
Karnaugh map for three variables-